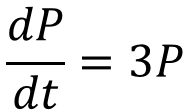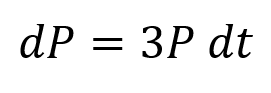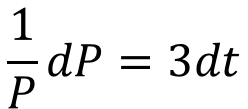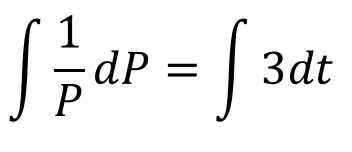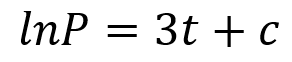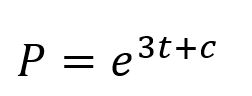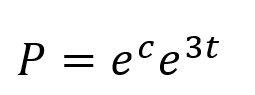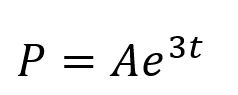Understanding Integration for Modeling Population Growth
Learn how to apply differential equations for modeling population growth scenarios using integration. The provided content guides you through solving equations to determine population size, rates of increase, and timeframes, with practical examples and step-by-step explanations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Teachings for Exercise 11K
Integration ?? ??= 3? You need to be able to use differential equations to model situations in context Multiply by ?? ?? = 3? ?? Divide by ? 1 ??? = 3?? 1 ??? = 3?? The rate of increase of a population P of micro organisms at time t, in hours, is given by: Write integrals Integrate (since we know that the population will be positive, we do not need the modulus sign) ?? ??= 3?, ? > 0 ??? = 3? + ? Inverse logarithm ? = ?3?+? Initially, the population was of size 8. This can be written as two powers of ? multiplied together ? = ???3? Since ? is a constant, so is ??. We can therefore write is as a single letter ? a) Find a model for ? in the form ? = ??3?, stating the value of ?. ? = ??3? 11K
Integration ? = ??3? You need to be able to use differential equations to model situations in context At time ? = 0, ? = 8 (8) = ??3(0) ?0= 1 The rate of increase of a population ? of micro organisms at time ?, in hours, is given by: 8 = ? We can now complete the formula ? = 8?3? ?? ??= 3?, ? > 0 ? = 8?3? Initially, the population was of size 8. a) Find a model for ? in the form ? = ??3?, stating the value of ?. 11K
Integration ? = 8?3? You need to be able to use differential equations to model situations in context Sub in ? = 2 ? = 8?3(2) Calculate ? = 3227.4 The rate of increase of a population ? of micro organisms at time ?, in hours, is given by: Round as instructed ? = 3200 ?? ??= 3?, ? > 0 ? = 8?3? Initially, the population was of size 8. b) Find, to the nearest hundred, the size of the population at the time ? = 2 11K
Integration ? = 8?3? You need to be able to use differential equations to model situations in context If the starting population is 8, we want to know when it will be 8000 8000 = 8?3? Divide by 8 1000 = ?3? The rate of increase of a population ? of micro organisms at time ?, in hours, is given by: Take natural logarithms of both sides ??(1000) = 3? Divide by 3 ??(1000) 3 = ? ?? ??= 3?, ? > 0 ? = 8?3? Calculate (and then convert into hours and minutes) 2.30 = ? Initially, the population was of size 8. So the time will be approximately 2 hours and 18 minutes c) Find the time at which the population will be 1000 times its starting value. 11K
Integration You need to be able to use differential equations to model situations in context The rate of increase of a population ? of micro organisms at time ?, in hours, is given by: ?? ??= 3?, ? > 0 ? = 8?3? Initially, the population was of size 8. It is not possible for a population to grow exponentially forever, since they will eventually start to run out of food or space d) State one limitation of this model for large values of ? 11K
Integration You need to be able to use differential equations to model situations in context ? ??= ?? ?? ? ?? Water in a manufacturing plant is held in a large cylindrical tank of diameter 20m. Water flows out of the bottom of the tank through a tap at a rate proportional to the cube root of the volume (of the water). 20? We are told how the volume of water changes with respect to time We can also create a formula linking the volume of the water to its height a) Show that after ? minutes after the tap is opened, ? some constant ?. 3 for ??= ? Think back to the differentiation chapter can we write ? product of other differentials? ?? as a 11K
Integration You need to be able to use differential equations to model situations in context ? ??= ?? ?? ? ?? Water in a manufacturing plant is held in a large cylindrical tank of diameter 20m. Water flows out of the bottom of the tank through a tap at a rate proportional to the cube root of the volume (of the water). ? = ??2 20? Sub in ? = 10 ? = ?(10)2 Simplify ? = 100? Differentiate a) Show that after ? minutes after the tap is opened, ? some constant ?. ?? ? = 100? 3 for ??= ? Invert ? ??= 1 ? ??= 1 100? 100? 11K
Integration You need to be able to use differential equations to model situations in context ? ??= ?? ?? ? ?? Water in a manufacturing plant is held in a large cylindrical tank of diameter 20m. Water flows out of the bottom of the tank through a tap at a rate proportional to the cube root of the volume (of the water). 20? ?? ??= So the rate of flow of water over time proportional to the cube root of the volume remaining ??= ? 3? ? Replace ? with the expression for volume in terms of ?? ?? is ?? 3??2 Sub in ? = 10 a) Show that after ? minutes after the tap is opened, ? some constant ?. This means that the rate of flow can be written as ? volume remaining ?? ??= ? ?? 3 for 3?(10)2 ??= ? 3? where ? is a constant to be found, and ? is the ??= ? Simplify 3100? ? ??= 1 ?? ??= ? It is negative since the rate of flow will be decreasing 3100? 100? Be careful here it is not ?3, the 3 is part of the cube root! 11K
Integration You need to be able to use differential equations to model situations in context ? ??= ?? ?? ? ?? Replace using the expressions we found 1 ? ??= ? 3100? 100? Water in a manufacturing plant is held in a large cylindrical tank of diameter 20m. Water flows out of the bottom of the tank through a tap at a rate proportional to the cube root of the volume (of the water). Separate the cube roots 1 ? ??= ? 3 3100? 20? 100? Group the constant terms 3100? 100? ? ??= ? 3 a) Show that after ? minutes after the tap is opened, ? some constant ?. So therefore: 3 for ??= ? ? ??= ? 3 , where ? =?3100? ? ??= 1 ?? ??= ? 100? 3100? 100? 11K
Integration ? ??= ? 3 Multiply by ?? You need to be able to use differential equations to model situations in context 3 ?? ? = ? Divide by 3 1 3 ? = ? ?? 1 3 ? = ? ?? Write as integrals Water in a manufacturing plant is held in a large cylindrical tank of diameter 20m. Water flows out of the bottom of the tank through a tap at a rate proportional to the cube root of the volume (of the water). Rewrite the left side as a power 1 3 ? = ? ?? 2 3 23 2 3= 2 Integrate both sides, remember to include a constant = ?? + ? Multiply both sides by 2 3 3?? +2 b) Show that the general solution to this differential equation may be written as = ? ?? and ? are constants 3? Cube both sides 3 3 2, where ? 2= 2 3?? +2 3? Square root both sides (think about how this affects the powers) 3 2 = 2 3?? +2 3? Swap the order of the terms inside the bracket 3 2 2 3? 2 = 3?? 11K
Integration 3 2 2 3? 2 You need to be able to use differential equations to model situations in context = 3?? Let 2 3? = ?, and 2 3? = ? 3 2 = ? ?? Water in a manufacturing plant is held in a large cylindrical tank of diameter 20m. Water flows out of the bottom of the tank through a tap at a rate proportional to the cube root of the volume (of the water). Note that since ? is a constant, so is 2 Note that since ? is a constant, so is 2 3? 3? b) Show that the general solution to this differential equation may be written as = ? ?? and ? are constants 3 2, where ? 11K
Integration 3 2 = ? ?? You need to be able to use differential equations to model situations in context When ? = 10, = 8, and we now know ? = 9 When ? = 0, = 27 3 2 3 2 8 = 9 ?(10) 27 = ? ?(0) Water in a manufacturing plant is held in a large cylindrical tank of diameter 20m. Water flows out of the bottom of the tank through a tap at a rate proportional to the cube root of the volume (of the water). = ? ?? = 9 0.5? Simplify Simplify 3 2 3 2 8 = 9 10? 27 = ? Cube root both sides Cube root both sides 1 2 1 2 2 = 9 10? 3 = ? Square both sides Square both sides 4 = 9 10? 9 = ? 3 2 3 2 Add 10?, subtract 5 10? = 5 Initially, the height of the water is 27m. 10 minutes later, the height is 8m. Divide by 10 ? = 0.5 c) Find the values of the constants ? and ? 11K
Integration 3 2 = 9 0.5? You need to be able to use differential equations to model situations in context We want to find ? when = 1 3 2 1 = 9 0.5? Cube root both sides 1 2 1 = 9 0.5? Water in a manufacturing plant is held in a large cylindrical tank of diameter 20m. Water flows out of the bottom of the tank through a tap at a rate proportional to the cube root of the volume (of the water). = 9 0.5? Square both sides 1 = 9 0.5? Subtract 9 8 = 0.5? Divide by -0.5 16 = ? 3 2 Initially, the height of the water is 27m. 10 minutes later, the height is 8m. d) Find the time in minutes when the water is at a depth of 1m 11K