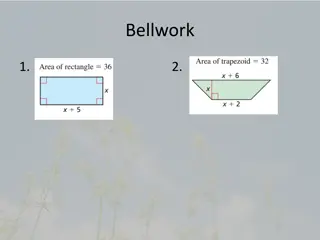
Exploring Square Numbers and Pythagorean Triplets
Introduction to square numbers, their properties, patterns, and Pythagorean triplets. Learn about non-perfect square numbers, rules for determining Pythagorean triplets, and solving related problems through examples and worksheets.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Chapter-1 Square And Square Roots Introduction The square of a number is that number raised to the power 2.Or Multiplying itself. A natural number n is called a perfect square or a square number if there exist a natural number m. such that n=m2. Some Properties and Patterns of Some Square Numbers 1. A number having 2, 3, 7 or 8 at unit s place is never a perfect square. Ex-142, 6593, 12347, are not perfect squares. 2. If a square number has 0, 1, 4, 5, 6, 9 respectively as its unit s digit, it must be a square of number with it s unit s place as 0, 1 or 9, 2 or 8, 5, 4 or 6, 3 or 7, respectively. Sometimes it s unit s digit may not be same but they are not be a square number like 21, 20, 24, 35, 26, etc. 3. The number of zeros at the end of a perfect square is always even. 4. Squares of even numbers are always even numbers and squares of odd numbers are always odd numbers. Ex- 22=4, 32=9 5. The square of a natural number other than one is either a multiple of 3 or exceeds a multiple of 3 by1. Ex- 32=9&42=15+1= 3 5+1 6. The square of a natural number other than one is either a multiple of 4 or exceed a multiple of 4 by 1. Ex- 42=16 & 72=48+1=4 12+1
7. 8. The sum of two consecutive triangular numbers is a square number. The difference of squares of two consecutive natural numbers is equal to their sum. Ex- 52 42= 5 + 4 = 9 72 62 = 7 + 6 =13 The square of a natural number n is equal to the sum of first n odd natural numbers. Ex- 12= 1 22= 1+3 32= 1+3+5 42= 1+3+5+7 52= 1+3+5+7+9 -------- --------- n2= 1+3+5+7+----------+n times odd number n2= 1+3+5+------------+(2n-1) 10. The square of a proper fraction is smaller than the fraction. Ex- (2/3)2= 4/9 then , 4/9<2/3 9.
There are 2n non-perfect square numbers between two consecutive square numbers n2and (n+1)2. Ex- Let n = 3, (n+1) = 3 + 1 = 4 n2=32= 9 (n+1)2 =42= 16 Number of non squares between 9 & 16 are (2n = 2 3 = 6). 10,11,12,13,14,15 which are six. A triplet ( m, n, p) of three natural numbers m, n, p is a Pythagorean triplet if m2+ n2= p2. For any natural number m greater than 1 ( 2m, m2 1, m2+1 ) is a Pythagorean triplet. If a,b,c are 3 natural numbers where a is the smallest one, then (i) if a is odd then sum of other two number is a2 and their difference is 1 (ii) if a is even then sum of other two numbers is a2 /2 and their difference is 2. Squares of natural numbers having all digits , follow the following pattern. 12 = 1 112 = 121 1112 = 12321 and so on. Another pattern 72 = 49 672= 4489 6672= 444889 11. 12. 13. 14. 15. 16.
Worksheet 1 Ex: (1) Find non-perfect square numbers between 72and 82. Solution: - 72and 82, here n=7 The non perfect square numbers in between 72and 82is 2n = 2 7 = 14. Similarly solve other sums. Question 8:- Whether all the options are Pythagorean triplet or not. Solution:- Let ( i ) ( 3, 4, 5) Here the lowest no. is 3 which is odd. Other nos. are 4 & 5 whose sum is 4 + 5 = 9 Hence, 32= 4 + 5 = 9 Also their difference is 5 4 = 1 As it satisfies the rule ( 3, 4, 5 ) is a Pythagorean triplet. Let ( ii ) ( 6, 8, 10 ) Here the lowest number is 6 which is even. Other two numbers are 8 & 10 whose sum is 8 + 10 = 18 Hence, 62 36 2=2 =10 + 8 = 18 Also their difference is 10 8 = 2 It satisfies the rule. So, (6, 8, 10 ) is a Pythagorean triplet. Other sums you can solve using properties.
Worksheet 2 All the sums of this worksheet solve using repeated subtraction method. Ex :- Find the square root of 81 using repeated subtraction method. Solution :- 81 1 = 80 Step - 1 80 3 = 77 Step - 2 77 5 = 72 Step - 3 72 7 = 65 Step - 4 65 9 = 56 Step - 5 56 11 = 45 Step - 6 45 13 = 32 ... Step - 7 32 15 = 17 Step - 8 17 17 = 0 . Step -9 / \_ 81 = 9
Worksheet -3 In this worksheet solve all the sums with prime factorisation method. Find square root of 24336 Factors of 24336 = 2 2 2 2 3 3 13 13 = = 2 2 3 13 = 4 3 13 = 12 13 = 156 = 156 Another question of worksheet-3 The area of square field is = 5184 m2 Side of the square field = 5184 5184 = = 2 2 2 3 3 = 8 9 = 72 Side of square = 72 m
Cont. of previous slide Length of the rectangle is twice of its breadth Let breadth = x m length = 2x m Perimeter of Rectangle = Perimeter of Square 2(l+b) = 4 side 2(2x+x) = 4 72 2 3x = 288 6x = 288 x = (288)/6 =48 breadth = 48m length = 2 48 = 96 Area of the Rectangle is l b = 96 48 = 4608 m2 Solve other worksheet Question with the help of Long division method
Ex-Which least number must be subtracted from 6203 it make a perfect square and also find the square root of the number so obtained. Here remainder is 274 which must be subtracted from 6203 to make it a perfect square The new number = 6203-274 = 5929 The square root of 5929 = = 77 Other Ex- Find the least number of six-digits which is a perfect square. Find the square root of the given number. The least six-digits number = 1,00,000 When we subtract 144 the result no. is less than the least six-digits no. So, we can take next no, that means we add 489 with 1,00,000 =1,00,000+489 =100489 Square root of 100489 is 317
Another example for finding square root of 3 correct upto three decimal places. Find the square root of 7 correct to two decimal places. Find the square root of 90 in estimation process. 81<90<100 92 <90<102 90 lies between 92 and 102 So, Let us take (9.5)2 = 9.5 9.5 = 90.25 But this is more than 90. Now we take another (9.4)2 = 88.36 Which means 88.36<90<90.25 Here 90.25 is much closer than 88.36 Hence = 90.5
Answers of Brain Teaser 1. A. a) The difference between the squares of two consecutive number is equal to their (ii) sum. b) The digit in the thousands place of (1111)2 is (ii) 4. c) Perfect squares cannot have 2,3,7 and 8 in its ones place. d) The smallest number by which 72 must be divided to make it a perfect square is (iv) 2. e) The square root of 3.052009 has (i) 3 decimal places B. a) The non-square numbers are there between 132 and 142 is 2x13 = 26 c) 5,7,9 is not a pythagorean triplet. Because 52 + 72 = 25+49 =74 which is not equal to 81 =92 . It does not satisfy the rule. another method here a = 5(odd) difference 9-7 = 2 which is not equal to 1. It also not satisfy the rule d) = 3 9 -1 = 8 8 3 = 5 5 5 = 0 e) Area of the square handkerchief is = 324 cm2 The side of the square = =18 cm
4. Smplify : (i) = = = = x = 10 (ii) + + = + + = 7+0.7+0.07 = 7.77 8. A General wishing to draw up his 64,019 men in the form of a square where he found 10 men extra. So, 64019-10 =64009 The number of men in front row = =253 253 men in the front row. HOTS 1. The cost of levelling a square lawn at Rs. 15 per square metre is Rs. 19,935 The are of the square lawn = = 1329 Side of the square lawn = Perimetre of the square lawn = 4 side Cost of fencing = Rs. 22 per metre Total cost required for fencing of the lawn = 4 side 22 Calculation part you can solve
2. If = 1.414 , = 2.236 and = 1.732 (i) + = + = = 6 + 4 = 6 1.414 + 4 1.732 = 8.484 + 6.928 = 15.412 +
Assignment Extra Question for ch-1 1. Find the square root of 18/5 correct upto two decimal places. 2. If the area of square field is 38.44 sqm. Then find the side of the square. 3. Find the least number by which 384 must be divided to make it a perfect square. 4. Find the least number, which must be added to 1825 to make it a perfect square. 5. Find the greatest 4- digit number which is a perfect square. 6. Find the value of (0.62)2 7. Find the length of the side of a square whose area is 441 m2 8. How many non-square numbers lie in between 81 and 225? 9. Find the square root of 10, correct to three decimal places. 10. Write pythagorean triplet if one number is 16. 11. 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row. 12. Find the square root of 7 upto three decimal places. 13. Find the square root of 800 by estimation method. 14. What is that decimal which when multiplied by itself 477.4225 15. Given that 2 = 1.414 and 5= 2.236, evaluate 36/5