Understanding Complex Numbers in Mathematics
Learn about complex numbers, including real and imaginary parts, operations with complex numbers, the imaginary unit, equality of complex numbers, and finding square roots of negative numbers. Explore how to define and use the imaginary unit, add, subtract, and multiply complex numbers, find complex solutions and zeros, and more.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
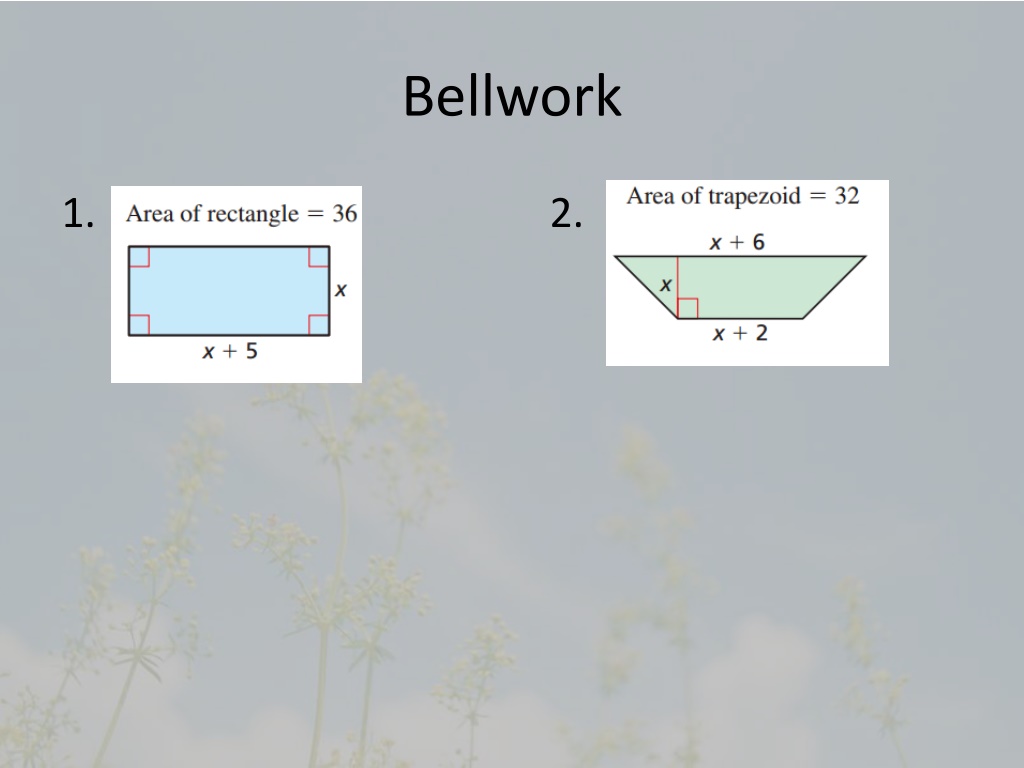
Bellwork 1. 2.
Complex Numbers Section 3.2
In your study of mathematics, you have probably worked with only real numbers, which can be represented graphically on the real number line. In this lesson, the system of numbers is expanded to include imaginary numbers. The real numbers and imaginary numbers compose the set of complex numbers.
What You Will Learn Define and use the imaginary unit i. Add, subtract, and multiply complex numbers. Find complex solutions and zeros.
The Imaginary Unit ? (Take Note) To overcome this problem, mathematicians created an expanded system of numbers using the imaginary unit ?, defined as ?. Note that ??= ?. ? = The imaginary unit ? can be used to write the square root of any negative number.
Finding Square Roots of Negative Numbers
Complex Number A complex number written in standard form is a number a + b ? where a and b are real numbers. The number a is the real part, and the number bi is the imaginary part. a + b ? If b 0, then a + b ? is an imaginary number. If a = 0 and b 0, then a + b ? is a pure imaginary number. The diagram shows how different types of complex numbers are related.
Equality of Two Complex Numbers (Take Note) Two complex numbers ? + ?? and ? + ?? are equal if and only if a = c and b = d. Find the values of x and y that satisfy the equation 2? 7? = 10 + ??.
Try you Practice packet 3.2 B side problem number: 5,7
Operation with Complex Number Take note
You Try Try you Practice packet 3.2 B side problem number:8,11
Try you Practice packet 3.2 B side problem number: 14, 15
Complex Solutions and Zeros Solving Quadratic Equations
Finding Zeros of a Quadratic Function Graph the function in your calculator