Unpacking the Associative Property of Multiplication in Elementary Classrooms
This study delves into how prospective teachers transform learned specialized content knowledge from professional development to elementary classrooms, focusing on the associative property of multiplication. The research explores the process of unpacking worked examples through representation uses and questioning, both in PD settings and in actual teaching environments. Theoretical frameworks and research questions guide the investigation, shedding light on the crucial role of sub-skills like representation use and deep questioning. Methods, participants, and task analyses provide insights into the study's structure and objectives.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Learning to Teach Fundamental Mathematical Ideas in Elementary Classrooms: The Case of the Associative Property Meixia Ding & Kayla Copeland Temple University Meixia.Ding@temple.edu Kayla.Copeland@temple.edu AERA, 2015
Introduction We explored the process of PTs transformation of the learned specialized content knowledge (SCK) from PD settings to elementary classrooms. Focused on the associative property (AP) of multiplication
Theoretical Framework SCK is a key component of mathematical knowledge for teaching. The core of SCK is to unpack a mathematical concept or learning goal, making it visible and learnable for students(Ball et al., 2008). A focus on teachers choice and use of examples may serve as a window on teachers SCK (Chick, 2009).
Theoretical Framework To unpack a worked example, teachers sub-skills such as representation uses and questioning are critical (Ball et al., 2008). Representation Use Make connections between concrete and abstract representations Concrete Abstract Questioning Deep questions elicit students self explanations
Research Questions (1) How do PTs learn to unpack worked examples through representation uses and questioning in PD settings? (2) How do PTs unpack worked examples through representation uses and questioning in the elementary classrooms?
Methods Participants: Anna, Cindy, & Kate Strong interests in learning to teach early algebra Varied in content knowledge and beliefs
Methods Part of a 1-year long study Setting Activity Content Discussed Time PD Summer training Research/textbook Textbook/lesson plan discussion 1 hour Pre-lesson study 2 hours Elementary classroom Enacted teaching NA 75 minutes Pre-teaching interview Lesson images 10-20 minutes Post-teaching interview Teacher reflections 20-30 minutes PD Post-lesson study Video-based discussions 1.5 hours
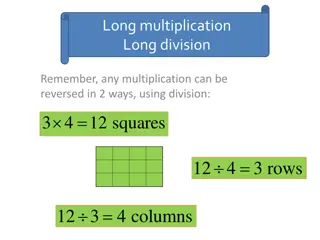
Task Analysis: Worked Example Upright bass strings come in sets of 4. Suppose one box holds 2 sets of strings. If a musician orders 3 boxes, how many strings will there be? Example of a concrete representation: BIG IDEA: Associative Property! (3 2) 4 3 (2 4) =
Task Analysis: Worked Example Textbook limitations: 4 3 2 cannot be explained based on meaning of multiplication. AP is directly presented.
Findings: PD setting PTs embraced teaching for meaning in summer training. PTs struggled with teaching for meaning in pre- lesson study. Likely due to the conflict with prior knowledge and experience. Instructor suggested using pictorial representations and insisted on questioning the meaning of each step.
Findings: Enacted Teaching Worked examples
Findings: Enacted Teaching Representation Use Worked Examples Concrete Only Concrete to Abstract Abstract Only Abstract to Concrete Anna String Kit Kat Counter Cindy Kit Kat String Kate Counter String
Findings: Enacted Teaching Teacher Responses Teacher Response Anna Cindy Kate R1 (Question) 27% (n=7) 44% (n=7) 33% (n=6) R2 (Accept) 19% (n=5) 25% (n=4) 33% (n=6) R3 (Defend) 23% (n=6) 6% (n=1) 6% (n=1) R4 (Explain) 27% (n=7) 19% (n=3) 28% (n=5) R5 (Ignore) 4% (n=1) 6% (n=1) 0% (n=0) Closer inspection: Asking for meaning of individual numbers Asking for number sentence with three numbers
Textbook Worked Example Anna s lesson Unpacking the string problem
Textbook Worked Example Cindy s lesson - A student explaining how he got 6 4
Textbook Worked Example Kate s lesson An incorrect interpretation of the AP
Conclusions Anna and Cindy made an effort in transforming the learned SCK, however, both lacked the ability to grasp students input to facilitate reasoning toward the expected direction. Experienced frustration Kate made the least amount of effort transforming what was discussed in the PD setting. Aimed to stress only procedures and was satisfied with her enacted lesson. Experienced the least amount of cognitive or emotional conflict.
Conclusions Challenges found in unpacking worked examples: Objective of AP not deemed as a goal Misconception: The more examples the better PTs demonstrated partial ability to transform subcomponents of SCK (representations & questioning). Missing representation connections Missing deep questioning PTs own knowledge and beliefs mattered in transformation of SCK.
