Understanding Survival/Event History Models in Panel Data Analysis
Introduction to survival/event history models in sociological research, covering types of outcomes, time-to-event data, key concepts for survival analysis, states, events, risk periods, and the significance of time in analyzing data.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
SC968: Panel Data Methods for Sociologists Introduction to survival/event history models
Types of outcome Continuous OLS Linear regression Binary Binary regression Logistic or probit regression Time to event data Survival or event history analysis
Examples of time to event data Time to death Time to incidence of disease Unemployed - time till find job Time to birth of first child Smokers time till quit smoking
Time to event data Set of a finite, discrete states Units (individuals, firms, households etc.) in one state Transitions between states Time until a transition takes place
4 key concepts for survival analysis States Events Risk period Duration/ time
States States are categories of the outcome variable of interest Each person occupies exactly one state at any moment in time Examples alive, dead single, married, divorced, widowed never smoker, smoker, ex-smoker Set of possible states called the state space
Events A transition from one state to another From an origin state to a destination state Possible events depend on the state space Examples From smoker to ex-smoker From married to widowed Not all transitions can be events E.g. from smoker to never smoker
Risk period 2 states: A & B Event: transition from A B To be able to undergo this transition, one must be in state A (if in state B already cannot transition) Not all individuals will be in state A at any given time Example can only experience divorce if married The period of time that someone is at risk of a particular event is called the risk period All subjects at risk of an event at a point in time called the risk set
Time Various meanings... Calendar time ...but onset of risk usually not simultaneous for all units Ex: by age 40, some individuals will have smoked for 20+ years, other for 1 year Duration=time since onset of risk ...intensity may not be the same EX: one smoker may smoke 5 cigarettes a day, another 20 1 unit of time -same for all individuals
Duration Event history analysis is to do with the analysis of the duration of a nonoccurrence of an event or the length of time during the risk period Examples Duration of marriage Length of life In practice we model the probability of a transition conditional on being in the risk set
Example data ID Entry date Died End date 1 01/01/1991 01/01/2008 01/01/1991 01/01/2000 01/01/2000 2 3 01/01/1995 01/01/2005 4 01/01/1994 01/07/2004 01/07/2004
Calendar time Study follow-up ended 1991 1994 1997 2000 2003 2006 2009
Censoring Ideally: observe individual since the onset of risk until event has occurred ...very demanding in terms of data collection (ex: risk of death starts when one is born) Usually incomplete data censoring An observation is censored if it has incomplete information Types of censoring Right censoring Left censoring
Censoring Right censoring: the person did not experience the event during the time that they were studied Common reasons for right censoring the study ends the person drops-out of the study We do not know when the person experiences the event but we do know that it is later than a given time T Left censoring: the person became at risk before we started observing her We do not know when the person entered the risk set EHA cannot deal with We know when the person entered the risk set condition on the person having survived long enough to enter the study Censoring independent of survival processes!!
Study time in years censored event censored event 0 3 6 9 12 15 18
Why a special set of methods? duration =continuous variable why not OLS? Censoring If excluding higher probability to throw out longer durations If treating as complete mis-measurement of duration Non normality of residuals Time varying co-variates Interested in the probability of a transition at any given time rather than in the length of complete spells Need to simultaneously take into account: Whether the event has taken place or not The length of the period at risk before the event ocurred
Survival function Length of time (duration) before an event occurs (length of spell -T) probability density function (pdf)- f(t) f(t)= lim Pr(t<=T<=t+ t) = F(t) t t 0 t cumulative density function (cdf)- F(t) F(t)= Pr( T<=t) = f(t) dt Survival function: S(t)=1-F(t)
Hazard rate h(t)= f(t)/ S(t) The exact definition & interpretation of h(t) differs: duration is continuous duration is discrete Conditional on having survived up to t, what is the probability of leaving between t and t+ t It is a measure of risk intensity h(t) >=0 In principle h(t)= rate; not a probability There is a 1-1 relationship between h(t), f(t), F(t), S(t) EHA analysis: h(t)= g (t, Xs) g=parametric & semi-parametric specifications
Data Survival or event history data characterised by 2 variables Time or duration of risk period Failure (event) 1 if not survived or event observed 0 if censored or event not yet occurred Data structure different: Duration is discrete Duration is continuous Assume: 2 states; 1 transition; no repeated events
Data structure-Discrete time ID Entry End date Event X at t0 X at t1 .... 1 01/01/1991 01/01/2008 01/01/2002 2 01/01/1991 01/01/2008 ID Date Duration (t) Event X 1 1 ... 1 2 ... 2 01/01/1991 01/01/1992 ..... 01/01/2002 01/01/1991 .... 01/01/2008 1 2 .... 11 1 .... 17 0 0 ..... 1 0 .... 0
Data structure-Discrete time The row is a an individual period An individual has as many rows as the number of periods he is observed to be at risk No longer at risk when Experienced event No longer under observation (censored) For each period (row)- explanatory variable X very easy to incorporate time varying co-variates Stata: reshape long
Data structure-continuous time ID Entry Died End date Duration Event X 1 01/01/1991 01/01/2008 17.0 2 01/01/1991 01/01/2002 3 01/01/1995 01/01/2000 5.0 0 0 3 01/01/2000 01/01/2005 01/01/2005 5.0 1 1 0 0 01/01/2002 11.0 1 0
Data structure-continuous time The row is a person Indicator for observed events/ censored cases Calculate duration= exit date entry date Exit date= Failure date Censoring date If time-varying covariates- Split the period an individual is under observation by the number of times time-varying Xs change If many Xs-change often- multiple rows
Worked example Random 20% sample from BHPS Waves 1 15 One record per person/wave Outcome: Duration of cohabitation Conditions on cohabiting in first wave Survival time: years from entry to the study in 1991 till year living without a partner
The data +----------------------------+ | pid wave mastat | |----------------------------| | 10081798 1 married | | 10081798 2 married | | 10081798 3 married | | 10081798 4 married | | 10081798 5 married | | 10081798 6 married | | 10081798 7 widowed | | 10081798 8 widowed | | 10081798 9 widowed | | 10081798 10 widowed | | 10081798 11 widowed | | 10081798 12 widowed | | 10081798 13 widowed | | 10081798 14 widowed | | 10081798 15 widowed | |----------------------------| Duration = 6 years Event = 1 Ignore data after event = 1
The data (continued) +----------------------------+ | pid wave mastat | |----------------------------| | 10162747 1 living a | | 10162747 2 living a | | 10162747 3 living a | | 10162747 4 living a | | 10162747 5 living a | | 10162747 6 living a | | 10162747 10 separate | | 10162747 11 . | | 10162747 12 . | | 10162747 13 . | | 10162747 14 never ma | | 10162747 15 never ma | +----------------------------+ Note missing waves before event
Preparing the data . sort pid wave . generate skey=1 if wave==1&(mastat==1|mastat==2) . by pid: replace skey=skey[_n-1] if wave~=1 . keep if skey==1 . drop skey . . stset wave,id(pid) failure(mastat==3/6) id: pid failure event: mastat == 3 4 5 6 obs. time interval: (wave[_n-1], wave] exit on or before: failure ------------------------------------------------------------------------------ 15058 total obs. 1628 obs. begin on or after (first) failure ------------------------------------------------------------------------------ 13430 obs. remaining, representing 1357 subjects 270 failures in single failure-per-subject data 13612 total analysis time at risk, at risk from t = 0 earliest observed entry t = 0 last observed exit t = 15 Select records for respondents who were cohabiting in 1991 Declare that you want to set the data to survival time Important to check that you have set data as intended
Checking the data setup . list pid wave mastat _st _d _t _t0 if pid==10081798,sepby(pid) noobs +-------------------------------------------------+ | pid wave mastat _st _d _t _t0 | |-------------------------------------------------| | 10081798 1 married 1 0 1 0 | | 10081798 2 married 1 0 2 1 | | 10081798 3 married 1 0 3 2 | | 10081798 4 married 1 0 4 3 | | 10081798 5 married 1 0 5 4 | | 10081798 6 married 1 0 6 5 | | 10081798 7 widowed 1 1 7 6 | | 10081798 8 widowed 0 . . . | | 10081798 9 widowed 0 . . . | | 10081798 10 widowed 0 . . . | | 10081798 11 widowed 0 . . . | | 10081798 12 widowed 0 . . . | | 10081798 13 widowed 0 . . . | | 10081798 14 widowed 0 . . . | | 10081798 15 widowed 0 . . . | +-------------------------------------------------+ 1 if observation is to be used and 0 otherwise time of entry time of exit 1 if event, 0 if censoring or event not yet occurred
Checking the data setup . list pid wave mastat _st _d _t _t0 if pid==10162747,sepby(pid) noobs +--------------------------------------------------+ | pid wave mastat _st _d _t _t0 | |--------------------------------------------------| | 10162747 1 living a 1 0 1 0 | | 10162747 2 living a 1 0 2 1 | | 10162747 3 living a 1 0 3 2 | | 10162747 4 living a 1 0 4 3 | | 10162747 5 living a 1 0 5 4 | | 10162747 6 living a 1 0 6 5 | | 10162747 10 separate 1 1 10 6 | | 10162747 11 . 0 . . . | | 10162747 12 . 0 . . . | | 10162747 13 . 0 . . . | | 10162747 14 never ma 0 . . . | | 10162747 15 never ma 0 . . . | +--------------------------------------------------+ How do we know when this person separated?
Trying again! . fillin pid wave . stset wave,id(pid) failure(mastat==3/6) exit(mastat==3/6 .) id: pid failure event: mastat == 3 4 5 6 obs. time interval: (wave[_n-1], wave] exit on or before: mastat==3 4 5 6 . --------------------------------------------------------------------------- --- 20355 total obs. 7524 obs. begin on or after exit --------------------------------------------------------------------------- --- 12831 obs. remaining, representing 1357 subjects 234 failures in single failure-per-subject data 12831 total analysis time at risk, at risk from t = 0 earliest observed entry t = 0 last observed exit t = 15
Checking the new data setup . list pid wave mastat _st _d _t _t0 if pid==10162747,sepby(pid) noobs +--------------------------------------------------+ | pid wave mastat _st _d _t _t0 | |--------------------------------------------------| | 10162747 1 living a 1 0 1 0 | | 10162747 2 living a 1 0 2 1 | | 10162747 3 living a 1 0 3 2 | | 10162747 4 living a 1 0 4 3 | | 10162747 5 living a 1 0 5 4 | | 10162747 6 living a 1 0 6 5 | | 10162747 7 . 1 0 7 6 | | 10162747 8 . 0 . . . | | 10162747 9 . 0 . . . | | 10162747 10 separate 0 . . . | | 10162747 11 . 0 . . . | | 10162747 12 . 0 . . . | | 10162747 13 . 0 . . . | | 10162747 14 never ma 0 . . . | | 10162747 15 never ma 0 . . . | +--------------------------------------------------+ Now censored instead of an event
Summarising time to event data Individuals followed up for different lengths of time So can t use prevalence rates (% people who have an event) Use rates instead that take account of person years at risk Incidence rate per year Death rate per 1000 person years
Summarising time to event data . stsum failure _d: mastat == 3 4 5 6 analysis time _t: wave exit on or before: mastat==3 4 5 6 . id: pid | incidence no. of |------ Survival time -----| | time at risk rate subjects 25% 50% 75% ---------+--------------------------------------------------------------------- total | 12831 .0182371 1357 . . . Number of observations Person-years <25% of sample had event by 15 elapsed years Rate per year stvary-check whether a variable varies within individuals and over time
Descriptive analysis To recap . pdf= probability that a spell has a length of exactly T f(t)= lim Pr(t<=T<=t+ t) = F(t) t t 0 t cdf=probability that a spell has a length<=T F(t)= Pr( T<=t) = f(t) dt Survival function S(t)=1-F(t)
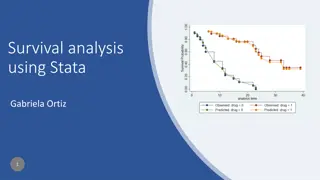
Kaplan-Meier estimates of survival time The Kaplan-Meier cumulative probability of an individual surviving to any time, t Analysis can be made by subgroup Nonparametric method First period: S1=1-d1/n1 exit rate After t periods: St=(1-d1/n1)*(1-d2/n2)* *(1-dt/nt) Survival function estimated only at times where you observe exits!!! Last t that can be estimated highest non-censored time observed
Survival/ failure function Describing the survival/ failure function . sts list, failure failure _d: mastat == 3 4 5 6 analysis time _t: wave exit on or before: mastat==3 4 5 6 . id: pid Beg. Net Failure Std. Time Total Fail Lost Function Error [95% Conf. Int.] ------------------------------------------------------------------------------- 2 1357 29 162 0.0214 0.0039 0.0149 0.0306 3 1166 33 89 0.0491 0.0061 0.0384 0.0625 4 1044 16 64 0.0636 0.0070 0.0513 0.0789 5 964 35 58 0.0976 0.0088 0.0818 0.1164 6 871 12 34 0.1101 0.0094 0.0931 0.1300 7 825 20 24 0.1316 0.0103 0.1128 0.1534 8 781 14 17 0.1472 0.0109 0.1271 0.1701 9 750 12 30 0.1609 0.0115 0.1398 0.1848 10 708 15 23 0.1786 0.0121 0.1563 0.2038 11 670 9 32 0.1897 0.0125 0.1666 0.2155 12 629 8 16 0.2000 0.0128 0.1762 0.2266 13 605 13 24 0.2172 0.0134 0.1922 0.2449 14 568 8 24 0.2282 0.0138 0.2025 0.2566 15 536 10 526 0.2426 0.0143 0.2160 0.2719 -------------------------------------------------------------------------------
Kaplan-Meier graphs Can read off the estimated probability of surviving a relationship at any time point on the graph E.g. at 5 years 88% are still cohabiting The survival probability only changes when an event occurs graph not smooth but (irregular) stepwise sts graph, survival
Kaplan-Meier survival estimate 1.00 0.75 0.50 0.25 0.00 0 5 10 15 analysis time
Kaplan-Meier survival estimate 1.00 0.75 0.50 0.25 0.00 0 5 10 15 time in years
Comparing survival by group using Kaplan-Meier graphs 1.00 0.75 0.50 0.25 0.00 0 5 10 15 analysis time sex = male sex = female
Testing equality of survival curves among groups The log-rank test A non parametric test that assesses the null hypothesis that there are no differences in survival times between groups
Log-rank test example . sts test sex, logrank failure _d: mastat == 3 4 5 6 analysis time _t: wave exit on or before: mastat==3 4 5 6 . id: pid Log-rank test for equality of survivor functions | Events Events sex | observed expected -------+------------------------- male | 98 113.59 female | 136 120.41 -------+------------------------- Total | 234 234.00 chi2(1) = 4.25 Pr>chi2 = 0.0392 Significant difference between men and women
More elaborate models Modeling the hazard rate not survival time directly h(t)=transitioning at time t, having survived up to t Time: Continuous- parametric Exponential Weibull Log-logistic Continuous-semi-parametric Cox Discrete Logistic Complementary log-log
Some hazard shapes Increasing Onset of Alzheimer's Decreasing Survival after surgery U-shaped Age specific mortality Constant Time till next email arrives
Proportional-hazards (PH) models h(t) is separable into h0(t) and the effects of Xs h0(t)= baseline hazard that depends on t but not on individual characteristics h(t)=h0(t)exp( X) Absolute differences in X proportional differences in h(t) ~scaling of h0(t)
Cox regression model Regression model for survival analysis Can model time invariant and time varying explanatory variables Produces estimated hazard ratios (sometimes called rate ratios or risk ratios) Regression coefficients are on a log scale Exponentiate to get hazard ratio Similar to odds ratios from logistic models
Cox regression equation (i) = + + + ( ) ( ) exp( ....... ) h t h t x x x 0 1 1 2 2 i i i n in ) (t hi is the hazard function for individual i ) ( 0t h is the baseline hazard function and can take any form It is estimated from the data (non parametric) , ,...., x x x are the covariates 1 2 i i in , ,...., are the regression coefficients estimated from the data 1 2 n PH assumption needed Estimate s without estimating h0(t) semi parametric model
Cox regression equation (ii) If we divide both sides of the equation on the previous slide by h0(t) and take logarithms, we obtain: ( ) h t = + + + i ln ....... x x x 1 1 2 2 i i n in ( ) h t 0 We call h(t) / h0(t) the hazard ratio The coefficients bi...bn are estimated by Cox regression, and can be interpreted in a similar manner to that of multiple logistic regression exp(bi) is the instantaneous relative risk of an event
Cox regression in Stata Will first model a time invariant covariate (sex) on risk of partnership ending Then will add a time dependent covariate (age) to the model