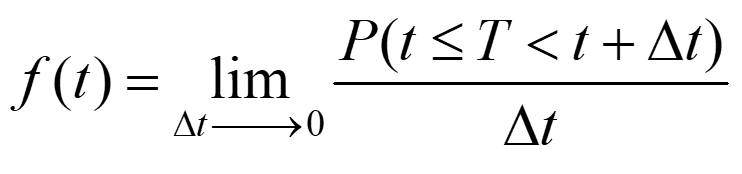Fundamentals of Survival Time Analysis
Understanding survival time analysis involves concepts like probability density functions, cumulative survival functions, the hazard function, and more. This analysis helps estimate and compare survival experiences in different groups, providing valuable insights into predicting outcomes in various scenarios.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Probability density function: f(t) The probability of the failure time occurring at exactly time t (out of the whole range of possible t s). unconditional failure rate + ( ) P t T t t = ( ) lim f t t 0 t 2
PDF 3
Survival Function or Curve Let T denote the survival time S(t) = P(surviving longer than time t ) = P(T > t) The function S(t) is also known as the cumulative survival function. 0 S( t ) 1 (t)=number of patients surviving longer than t total number of patients in the study
Survival function: 1-F(t) The goal of survival analysis is to estimate and compare survival experiences of different groups. Survival experience is described by the cumulative survival function: F(t) is the CDF of f(t), and is more interesting than f(t). = = ( ) 1 ( ) 1 ( ) S t P T t F t Example: If t=100 years, S(t=100) = probability of surviving beyond 100 years. 6
Cumulative survival Same hypothetical data, plotted as cumulative distribution rather than density: Recall pdf: 7
Cumulative survival P(T>20) P(T>80) 8
Hazard Function: new concept AGES Hazard rate is an instantaneous incidence rate. 9
Hazard function + ( / ) P t T t t T t = ( ) lim h t t 0 t ( ) f t = Hazard from density survival and : (t) h ( ) S t Derivation (Bayes rule): + + ( & ) ( ) ( ) t P t T t dt T t P t T t dt f t dt = + = = = ( ) ( / ) h t dt P t T t dt T t ( ) ( ) ( ) P T t P T t S 10
Hazard function The hazard function is also known as the Instantaneous failure mortality, conditional mortality rate, and age-specific failure rate. rate, force of 11
Hazard Curve 12
Example 2.1 13
Hazard vs. density This is subtle, but the idea is: When you are born, you have a certain probability of dying at any age; that s the probability density (think: marginal probability) Example: a woman born today has, say, a 1% chance of dying at 80 years. However, as you survive for awhile, your probabilities keep changing (think: conditional probability) Example, a woman who is 79 today has, say, a 5% chance of dying at 80 years. 15
A possible set of probability density, failure, survival, and hazard functions. f(t)=density function F(t)=cumulative failure h(t)=hazard function S(t)=cumulative survival 16
A probability density we all know: the normal distribution What do you think the hazard looks like for a normal distribution? Think of a concrete example. Suppose that times to complete the midterm exam follow a normal curve. What s your probability of finishing at any given time given that you re still working on it? 17
f(t), F(t), S(t), and h(t) for different normal distributions: 18
Examples: common functions to describe survival Exponential (hazard is constant over time, simplest!) Weibull (hazard function is increasing or decreasing over time) 19
f(t), F(t), S(t), and h(t) for different exponential distributions: 20
f(t), F(t), S(t), and h(t) for different Weibull distributions: Parameters of the Weibull distribution 21
Exponential = ( ) h t h Constant hazard function: ht = = = ( ) ( ) P T t f t he Exponential density function: Survival function: hu hu ht ht = = = = = ( ) ( ) 0 P T t S t he du e e e t 22 t
Why isnt the cumulative probability of survival just 90% (rate of .01 for 10 years = 10% loss)? With numbers cases/pers 1 0 . = ( ) on year h t Incidence rate (constant). Probability of developing disease at year 10. 01 . 1 . 10 ( ) = = = = ( 10 ) 01 . 01 . 0.009 P t e e Probability of surviving past year 10. 01 . t = = ( ) 90 5 . % S t e (cumulative risk through year 10 is 9.5%) 23
Example Recall this graphic. Does it look Normal, Weibull, exponential? 24
Example One way to describe the survival distribution here is: P(T>76)=.01 P(T>36) = .16 P(T>20)=.20, etc. 25
Example Or, more compactly, try to describe this as an exponential probability function since that is how it is drawn! Recall the exponential probability distribution: If T ~ exp (h), then P(T=t) = he-ht Where h is a constant rate. Here: Event time, T ~ exp (Rate) 26
Example To get from the instantaneous probability (density), P(T=t) = he-ht, to a cumulative probability of death, integrate: ( ) h t = = P(T t) he t ( ) ( ) h t h t = = P(T ) t 1 he e Area to the left 0 ( ) ( ) h t h t = = ( ) 1 1 ( ) P T t e e Area to the right 27
Example ( ) h age = ( ) P T age e Solve for h: 36 h( ) = 0 16 . e = ln 16 (. 36 ) h ln 16 (. ) = h 36 05 . h 28
Example . 05 ( ) age = ( ) P T age e This is a parametric survivor function, since we ve estimated the parameter h. 29
Hazard rates could also change over time = ( ) 0 . = 1 * t h t Example: Hazard rate increases linearly with time. h(5) .05 = h(10) .1 30
Relating these functions (a little calculus just for fun ): ( ) f t = Hazard from density survival and : (t) h ( ) S t = Survival from density S(t) : ( ) f u du t ( ) dS t = Density from survival ( f : ) t dt t 0 ( ( ) ) h u du = Density from hazard ( f : ) ( ) t h t e t 0 ( ( ) ) h u du = Survival from hazard S(t) : e d = Hazard from survival : (t) - ln ( ) h S t dt 32
Getting density from hazard = ( ) 0 . = 1 * t h t Example: Hazard rate increases linearly with time. h(5) .05 = h(10) .1 t ( ( ) ) h u du = Density from hazard ( f : ) ( ) t h t e 0 t t ( 01 . ) . 01 tdu udu 2 005 . t = = = ( f ) . 01 * . 01 ( ) . 01 ( ) t te t e t e 0 0 . 005 ( 25 ) . 125 = = = = ( ) 5 . 01 ) 5 ( 05 = . . 044 f t e e 005 . 5 . 100 ( ) = ( 1 . = = ( 10 ) 10 ) 1 . . 06 f t e e 33
Getting survival from hazard = ( ) 0 . = 1 * t h t h(10) .1 = h(5) .05 t ( ( ) ) h u du = Survival from hazard : S(t) e 0 t ( 01 . ) udu 2 . 005 t = = S(t) e e 0 005 . 100 ( ) = = 10 ( ) = . 60 S e . 005 ( 25 ) = ) 5 ( S . 88 e 34