Understanding Rounding and Significant Figures in Calculations
Rounding is done to limit the precision of numbers, ensuring they are not overly specific. When rounding, the last digit to be removed determines whether to round up or down. If the digit is 5 and there are non-zero numbers following it, you round up; otherwise, you round to the nearest even number. Following specific rules for sig figs in calculations for both multiplication/division and addition/subtraction ensures the accuracy of your results.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
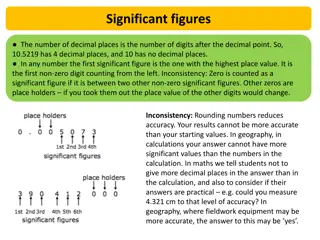
Part 04 Rounding and Sig figs in Calculations page 25-26
What is the purpose of rounding? To limit the precision of a number. To make a number less specific. When you limit the precision of a number you need to start removing digits from right to left. When you get to the last digit to removed, that digit will indicate whether to round up or down. 5.7 For example, round 5.66 to one decimal place. Rounded up For example, round 5.64 to one decimal place. 5.6 Rounded down These rounded numbers make sense because the answer is as close to the actual number as possible.
What happens when the last removed digit is a 5, which is not closer to rounding up or down? First, if there are any nonzero numbers to the right of this 5, then round up. This makes sense because this number is closer to the rounded up number If the last removed digit is a 5 and no nonzero numbers after it then ??? Then round to the even number. This makes it 50/50 up/down. For example, round 5.65 to one decimal place. 5.6 Rounded down For example, round 5.6500001 to one decimal place. 5.7 Rounded up
Round the following to three sig figs. 569 0.896 0.00680 569.4 0.89560 0.0068 500.1 5604 0.9999 1 4.56098 x 105 25650 500. 0 56 _ 0 1.00 1.00 4.56 x 105 25600
Sig figs in Calculations When multiplying/dividing, the answer must contain the same number of sig figs as the measurement with the LOWEST number of significant figures. 19.2 cm2 5.50 cm x 3.500cm = 170000 m3 (55 m)3 = 02801 . 0 3 ( ) mm 10 mm = 2 x 10-8 mm 6 . 5 00 x mm
Sig figs in Calculations When adding/subtracting, the answer must contain the same precision as the measurement with the LOWEST precision. Usually lowest precision = lowest number of decimal places. 5.50 cm 3.500 cm = 2.00 cm 35.55 m + 0.0044 m = 35.55 m 2400 ft. + 565 ft. = 3000 ft.
Sig figs in Calculations Exact numbers have an infinite number of sig figs so they are never the LOWEST sig figs or precision. You can ignore them when finding the lowest. Exact numbers are counting numbers like how many students are in the class right now. Also, defined numbers like there are 12 inches in 1 ft or 60 seconds in 1 minute.
Assignment Worksheets 02 and 03: p 7-8