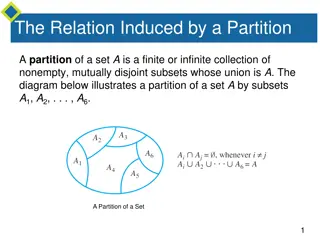
Understanding Recurrence Relations and Applications
Recurrence relations define functions based on previous values and are commonly used in algorithmic analysis. Examples include calculating savings account balances and analyzing binary search algorithms using induction. The concept is further explored in the context of merge sort time complexity.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Recurrence Relations Recursive definition of functions
Definition 6.11 (Recurrence relation) A recurrence relation (sometimes simply called a recurrence) is a function T(n) that is defined (for some n) in terms of the values of T(k) for input values k < n. There must be a base case, typically T(0) or T(1) Example: T(0) = 1 and T(n) = n*T(n-1) What is T(n)? T(1) = 1* T(0) = 1 T(2) = 2* T(1) = 2*1 T(3) = 3* T(2) = 3*2*1 T(4) = 4* T(3) = 4*3*2*1 T(n) = n!
Savings account: Deposit $1000 every year; Interest rate is 2% per year T(0) = 1000 T(n) = 1.02*T(n-1) + 1000. Claim P(n): T(n) = 51000 * 1.02n 50000 Proof by induction: 1. base case n = 0, 51000 * 1.020 50000 = 1000 2. Assume P(n-1): T(n-1) = 51000 * 1.02n-1 50000 3. T(n) = 1.02*T(n-1) + 1000 4. = 1.02*(51000 * 1.02n-1 50000) + 1000 5. = 51000 * 1.02n 1.02*50000 + 1000 6. = 51000 * 1.02n 51000 + 1000 7. = 51000 * 1.02n 50000 8. P(n-1)->P(n) 8. By induction (1 and 8): for n >= 0, T(n) = 51000 * 1.02n 50000 rec def 2,3 substitution algebra algebra algebra 2-7
Apply to Algorithmic Analysis Binary Search. T(1) = 2c T(n) = T(n/2) + c if n is even, T((n-1)/2 ) + c if n is odd. some constant c Claim T(n) = c* floor(log2(n)) + 2c Base case: T(1) = 2c , and c* floor(log2(1)) + 2c = 2c, since log(1) = 0
Induction: 1. Assume true for any 1<=k<n Case 1: assume n is odd. 2. T(n) = T((n-1)/2) + c 3. T(n) = c* floor(log2((n-1)/2)) + 2c + c 1, substitution 4. T(n) = c* floor(log2(n-1)-1) + 2c + c 5. T(n) = c* floor(log2(n-1)) + 2c 6. T(n) = c* floor(log2(n)) + 2c 7. P(k) for any 1<=k<n => P(n) 8. By strong induction, the result follows for n odd recurrence log2(1/2) = -1 simplification floor(log2(n)) = floor(log2(n-1)) since n is odd 1-6 Case 2: n is even has a similar proof. T(n) is Q(log n)
If T(n) is the time for merge sort, then T(1)=c T(n)=T( n/2 )+T( n/2 )+cn
To get an idea of what T(n) is we look at the recursion tree split list, merge n items split , merge n/2 items split , merge n/2 items split , merge n/4 split , merge n/4 split , merge n/4 split , merge n/4 Single items x x x x . x x x x
How much work at each node? Some constant amount, d, to change indices to split the list for each node Some constant, c, times the number in each sublist to merge from list below How much work at each level? Since there are n/2k in each sublist at a level and 2k sublist, the merges take cn time for the whole level, the other work takes d 2k where 2k < n, so we estimate the time as cn (changing c to account for the d) How many levels? log2(n) for n a power of 2 So we see that we expect T(n) to be O(n log2(n)) Formal proof requires solving the recurrence
If T(n) is the time for merge sort, then T(1)=c and T(n)=T( n/2 )+T( n/2 )+cn First we prove T(n) = O(n log2(n)) for n = 2k,using induction. Base case: T(1) = c is given. Induction:1. assume T(m)=T( m/2 )+T( m/2 )+cm for all 1 <= m < n 2. T(n) = T(2k) = T(n/2)+T(n/2)+cn (since n is power of 2 don t need , ) rec 3. T(n) = T(2k) = 2T(2k-1)+c 2k Now we shift gears to a related recurrence: let R(k) = T(2k) , then 3 gives us 4. R(k) = 2R(k-1) + c 2k and we have R(0) = T(1) = c, so we first solve for R
R(k) = 2R(k-1) + c 2k and we have R(0) = c Let s get the pattern k R(k) 0 c 1 2c + 2c = 4c 2 8c + 4c = 12c 3 24c + 8c = 32c 4 64c + 16c = 80c 5 160c + 32c = 192c
R(k) = 2R(k-1) + c 2k and we have R(0) = c Let s get the pattern k R(k) 0 c 1 2c + 2c = 4c 2 8c + 4c = 12c 3 24c + 8c = 32c 4 64c + 16c = 80c 5 160c + 32c = 192c We have discovered a pattern! Conjecture: R(k) = (k+1) 2k c, for all k >= 0 = (k+1) 2k c = (k+1) 2k c = (k+1) 2k c = (k+1) 2k c = (k+1) 2k c = (k+1) 2k c = 1*1c = 2*2c = 3*4c = 4*8c = 5*16c = 6*32c
R(k) = 2R(k-1) + c 2k and we have R(0) = c To prove by induction: R(k) = (k+1) 2k c, for all k >= 0 Base case: on previous page we showed this is true for k = 0 1. Assume R(k-1) = k 2k-1 c, for any k > 0 induction assumption 2. R(k) = 2R(k-1) + c 2k 3. R(k) = 2k 2k-1 c + c 2k 4. R(k) = k 2k c + c 2k 5. R(k) = (k+1) 2k c 6. (R(k-1) = k 2k-1 c, for any k > 0) => R(k) = (k+1) 2k c 1-5 7. By induction: R(k) = (k+1) 2k c, for all k >= 0 base case and 6 recurrence 1, 2 substitution simplification simplification Now return to our original T(n)
We let R(k) = T(2k) = T(n) (n a power of 2) We concluded R(k) = c(k+1) 2k, for all k >= 0 To finish the proof for T, k = log2(2k) = log2 (n), so T(n) = R(log2 (n)) = cn(log2 (n) + 1) So for n a power of 2, we have T(n) = Q(n log n) What about n not a power of 2? Choose an integer p such that 2p-1 < n <= 2p Since T is a non-decreasing function, T(2p-1) <= T(n) <= T(2p) T(n) <= T(2p) = c2p(log2 (2p) + 1) <= 2cn(log2 (2n) + 1) = 2cn(log2 (n) + 2) = 2cnlog2 (n) + 4cn is O(n log2(n)) T(n) >= T(2p-1) = c2p-1(log2 (2p-1) + 1) >= c(n/2) (log2 (n/2) + 1) = (c/2) n log2 (n) + cn/2 is W (n log2(n)) T(n) is Q(n log n)
The Master method applies to many divide and conquer algorithms. Theorem 6.10 (Master Theorem) Consider the recurrence T(1) = c T(n) = a T(n/b)+c nk for constants a 1, b > 1, c > 0, and k 0. Then: Case (i), the leaves dominate : if bk< a, then T(n)= (nlogb(a)) Case (ii), all levels are equal : if bk= a, then T(n) = (nk log n) Case (iii), the root dominates : if bk> a, then T(n) = (nk).
Example 1: Binary Search time : T(1) = c T(n) = T(n/2) + c if n is even, T((n-1)/2) if n is odd Fits with a = 1, b = 2, k = 0 bk = 1 = a, so case 2: T(n) = Q(nk log n) = Q(log n) Example 2: Mergesort. T(1)=c and T(n)=2 T(n/2) + cn Fits with a = 2, b = 2, k = 1 bk = 2 = a, so case 2: T(n) = Q(nk log n) = Q(n log n)
T(n) = 4 T(n/4) + c n2 Example: T(1) = c a = 4, b = 4, k = 2 bk = 16 > a, case 3: T(n) = Q(nk) = Q(n2) T(n) = 4 T(n/2) + c n2 Example: T(1) = c a = 4, b = 2, k = 2 bk = 4 = a, case 2: T(n) = Q(nklog n) = Q(n2log n) Example: T(1) = c a = 9, b = 3, k = 1 bk = 3 < a, case 1: T(n) = 9 T(n/3) + c n T(n) = Q(nlogb a) = Q(nlog3 9) = Q(n2)