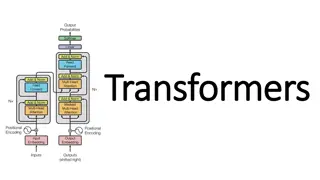
Understanding Multi-Head Attention Layers in Transformers
Sitan Chen from Harvard presents joint work with Yuanzhi Li exploring the provable learnability of a multi-head attention layer in transformers. The talk delves into the architecture of transformers, highlighting the gap between practical success and theoretical understanding. Preliminaries, prior work, algorithm outline, and proof sketches are discussed alongside single-head and multi-head attention mechanisms. The session serves as a clean sandbox for rigorous study on the learnability of transformer functions, with a focus on provable results after years of theoretical research on feedforward architectures. Theory for learning transformers could potentially reshape our understanding significantly.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
PROVABLY LEARNING A MULTI-HEAD ATTENTION LAYER SITAN CHEN HARVARD BASED ON JOINT WORK W/ YUANZHI LI (CMU / MSR)
TRANSFORMERS Architecture behind state-of-the-art approaches to NLP and vision Wildly successful in practice, poorly understood in theory This talk: clean sandbox where we can hope to rigorously study learnability of these functions, first provable learnability results Comes in wake of ~10 yrs of theoretical work on learning feedforward architectures (for which many mysteries still remain!) Outlook: theory for learning transformers could shape out very differently!
Preliminaries and setup Prior work and our results Algorithm outline Proof sketch
SINGLE-HEAD ATTENTION Given: input sequence? ? ?(sequence of ? tokens in ?), attention matrix? ? ? projection matrix? ? ? The quick brown fox jumps over the lazy dog The quick brown fox jumps over the lazy dog (applied row-wise) ? ? = softmax ??? ?? ?-th row of ? ? : ( ??,?? ?) softmax ?? ??,?1 ? ??,?2 ???,?3 ?
MULTI-HEAD ATTENTION Given: input sequence? ? ?(sequence of ? tokens in ?), attention matrices?1, ,?? ? ? projection matrices?1, ,?? ? ? ? softmax ???? ??? ? ? = ?=1
MULTI-HEAD ATTENTION Generalizes what is typically used in practice: ? ????1 ? ????? ??1 ??? ?, ,softmax ??? ??? ? ? = concat softmax ??1 from The Illustrated Transformer
A SANDBOX Prior theory for transformers: Representational power [Dehghani et al. 18], [Yun et al. 20], [Bhattamishra-Ahuja-Goyal 20], .. Sample compl. [Wei-Chen-Ma 21], [Edelman-Goel-Kakade-Zhang 22] Dynamical systems / neural ODE [Geshkokvski-Letrouit-Polyanskiy- Rigollet 23a, 23b] Training a single attention head for simple synthetic tasks [Jelassi- Sander-Li 22], [Li-Wang-Liu-Chen 23], [Oymak-Rawat- Soltanolkotabi-Thrampoulidis 23], [Tian-Wang-Chen-Du 23], [Li-Li- Risteski 23] Training a linearized multi-head attention layer [Fu-Guo-Bai-Mei 23], [Deora-Ghaderi-Taheri-Thrampoulidis 23]
A SANDBOX Today: Can we efficiently learn if all we assume is 1) The data comes from a nice distribution 2) It can be perfectly labeled by a multi-head attention layer? Unlike prior settings, not even clear if we have any provable algorithm, let alone an end-to-end analysis of gradient descent
? softmax ???? ??? ? ? = REALIZABLE PAC LEARNING ?=1 Input: sequence-to-sequence pairs ?1,?1, , ??,?? where ?? ?, ??= ? ?? Output: multi-head attention layer ? such that w.h.p. over randomness of the samples and algorithm, 2 ? ?? ? ? ? ? ? Real-world tokens are discrete. As a (highly stylized) proxy, we consider ? = Unif 1,1? ? but can also handle ? = ? 0,Id (analysis there is strictly easier for us)
Preliminaries and setup Prior work and our results Algorithm outline Proof sketch
PRIOR WORK ON FEED-FORWARD NETWORKS Long line of work on PAC learning feed-forward networks (mostly focusing on one-hidden-layer networks) ? ? ? = ??? ??,? ?=1 Almost exclusively considers input distribution given by ? 0,Id State of the art: [C-Narayanan 23]:poly ?,1/?? ?2-time proper learner [Diakonikolas-Kane 23]:poly ?,1/?? ?-time improper learner [C-Klivans-Meka 21]: poly ? exp(poly size,Lipschitzness,1/? )-time proper learner for deep networks
PRIOR WORK ON FEED-FORWARD NETWORKS These all exploit some subset of the following features specific to feedforward networks + Gaussianity assumption ?(?) only depends on a low-dimensional projection of ?, namely to the span of ?1, ,?? --- Projections of ? 0,Id to orthogonal subspaces are independent --- product + rotation invariance multi-index model for any ?, ker ? ? ? ?? Id Joint distribution over ?,? ? has e.g. exists tensor-valued polynomial ? s.t. ? ? ? ? ? contains all irrelevant directions useful moment structure ????? = ?=1
PRIOR WORK ON FEED-FORWARD NETWORKS What about for? ? = ?=1 ?softmax ???? ???? multi-index model ---? ?does not only depend on low-dim projection product + rotation invariance ---specific to Gaussian distribution useful moment structure --- ? softmax ??? = ??? What are the structural properties of multi-head attention that enable efficient learning?
? ?: # heads ?: # tokens softmax ???? ??? ? ? = OUR RESULTS ?=1 We only consider small ? (at most logarithmic in ?), and ? ? ? Thm [C-Li 24]: There is a ?? ??-time algorithm for PAC learning nice multi-head attention layers over uniformly random Boolean examples to error ? ?. To our knowledge, no such result was known even for ? = 1 Thm [C-Li 24]: For general multi-head attention layers, even for ? = 2: [SQ lower bound]: Any statistical query alg. requires ?? ? queries/inv. tolerance [Crypto lower bound]: Assuming LWE variant, cannot be done in poly ?,?,? time
? ?: # heads ?: # tokens softmax ???? ??? ? ? = FINE PRINT ?=1 We only consider small ? (at most logarithmic in ?), and ? ? ? Attention matrices: for all ?,? ? , Incoherence: ??,?? 1 ?? ? ?? ? poly ?,log ? removing these would require new ideas Stable rank not too small: r ?? ? Diagonals not too heavy: Tr ?? 2/ ?? op 2 poly ?,?,log ? so that diagonal entries of softmax don t behave differently from off-diagonals log? ?? ? Columns not too heavy: Non-arithmetic: entries are somewhat far from any lattice ?? :,?2 ? ??? ? for handling quirks of Boolean input distribution (e.g. lack of anti-concentration) can probably handle more diverse norms with (a lot) more work Norms comparable + bounded: ?? ? 2 ?? ? 2 polylog ? ,?? ?
? ?: # heads ?: # tokens softmax ???? ??? ? ? = FINE PRINT ?=1 We only consider small ? (at most logarithmic in ?), and ? ? ? Projection matrices: for all ?,? ? , Incoherence: ??,?? 1 ??? ? ?? ? much milder than for ? s, but removing would still require Stable rank not too small: ?? ? 2 poly ?,?,log ? 2 ?? op new ideas much milder than for ? s, can probably remove with more work Norms not too different: ?? ? 2, where r is stable rank of ? s 2 r ?? ?
Preliminaries and setup Prior work and our results Algorithm outline Proof sketch
? softmax ???? ??? ? ? = ALGORITHM OUTLINE ?=1 1. Crudely estimate ??? 2. Crudely estimate affine hull ? of ?? s: ? ?????: ???= 1 3. Refine estimate for ??? 4. Refine estimate for ? 5. Estimate span ?1, ,?? 6. Epsilon-net over span ?1, ,?? to learn ?
? softmax ???? ??? ? ? = ALGORITHM OUTLINE ?=1 1. Crudely estimate ??? 2. Crudely estimate affine hull ? of ?? s: ? ?????: ???= 1 3. Refine estimate for ??? 4. Refine estimate for ? hardest part of the analysis 5. Estimate span ?1, ,?? 6. Epsilon-net over span ?1, ,?? to learn ?
? softmax ???? ??? ? ? = ALGORITHM OUTLINE ?=1 1. Crudely estimate ??? hardest part of the analysis
Preliminaries and setup Prior work and our results Algorithm outline Proof sketch
? softmax ???? ??? ? ? = ESTIMATING ??? ?=1 Lemma: If we train a single attention head softmax ??? ?? with ? initialized to ?? ? with a single step of gradient descent on ?w.r.t ? ? ? softmax ??? ??? then the resulting ? is 1/poly r -close in Frobenius norm to ?W? 2, More succinctly, 1 ?? ? ?? ?? ??? Recall ? = ?=1 ?softmax ???? ???, so by linearity suffices to show 1 ?? ? ?? ? softmax ???? ??? ??
? softmax ???? ??? ? ? = ESTIMATING ??? ?=1 Lemma: If we train a single attention head softmax ??? ?? with ? initialized to ?? ? with a single step of gradient descent on ?w.r.t ? ? ? softmax ??? ??? then the resulting ? is 1/poly r -close in Frobenius norm to ?W? 2, More succinctly, 1 ?? ? ?? ?? ??? Recall ? = ?=1 ?softmax ???? ???, so by linearity suffices to show 1 ?? ? ?? ? softmax ???? ? ???
? softmax ???? ??? ? ? = ESTIMATING ??? ?=1 1 ?? ? ?? ? softmax ???? ? ??? Intuition: if the inner softmax concentrated tightly around its expectation ? ? softmax ???? , then the above would be 1 ?? ? ?? ? ? ? = ??? 1 ?Tr 1? ? ? = ???
? softmax ???? ??? ? ? = ESTIMATING ??? ?=1 Unfortunately, we don t in general have such good concentration Example: ? 0,0.01200 200 expectation reality Instead, we argue that, conditioned on the Hamming weight of fixed substrings of ?,conditional expectation of softmax concentrates
? softmax ???? ??? ? ? = ALGORITHM OUTLINE ?=1 1. Crudely estimate ??? 2. Crudely estimate affine hull ? of ?? s: ? ?????: ???= 1 3. Refine estimate for ??? 4. Refine estimate for ? hardest part of the analysis 5. Estimate span ?1, ,?? 6. Epsilon-net over span ?1, ,?? to learn ?
? softmax ???? ??? ? ? = ALGORITHM OUTLINE ?=1 2. Crudely estimate affine hull ? of ?? s: ? ?????: ???= 1 hardest part of the analysis
? softmax ???? ??? ? ? = SCULPTING THE AFFINE HULL ?=1 Let ?denote our crude estimate for ??? Suppose in every head, first token attended to other tokens in same way ? ?? ? ? ? softmax ?1,:??? ???= ? ? ?1,:= ? ? then ?1,: linear combination of ? rows of ? ? Approx. converse holds, letting us detect/certify when this happens
? softmax ???? ??? ? ? = SCULPTING THE AFFINE HULL ?=1 Let ?denote our crude estimate for ??? Suppose in every head, first token attended to other tokens in same way ? If softmax ?1,:?? = ?, then for every ?,? [?], ?1,:?? ? ?1,:?? ?= ln ??/?? This yields an affine constraint on every attention matrix ?
? softmax ???? ??? ? ? = SCULPTING THE AFFINE HULL ?=1 So if we saw many examples ?,?for which the first row of every attention pattern is the same across heads: We can detect every time this happens, yields affine constraint on ?? s With enough such examples, can solve to obtain the affine hull of ?? s Why are the set of possible affine constraints obtainable in this fashion sufficiently diverse that we can learn the affine hull? Technically can only certify when first rows are approximately equal approximation error dictated by how accurate ? was How long do we have to wait before seeing enough such examples?
APPROXIMATION ERRORS: ISSUE #1 Suppose we wanted to learn the affine hull to error ? need to certify all first rows of attention patterns are poly ? -close this happens with probability ? ? over Gaussian examples traditional CLT-based estimates have error 1/ ? for Boolean examples, this bottlenecks us at ? ? 1/? even if we have exact access to ??? Must use a suitable local CLT to avoid the 1/ ? bottleneck (this is where non-arithmetic assumption comes in)
APPROXIMATION ERRORS: ISSUE #2 Recall that we only have ??? up to error 1/poly r bottlenecks our error in estimating the affine hull at 1/poly r Issue: Even if r = ?, the exponent in this polynomial is not large enough Given membership query access to a convex body in ? which is ?- pointwise-close to the affine hull for ? 1/ ?, unclear how to estimate the span of the affine hull, even when the span is just 1-dimensional To refine ?, we first obtain a crude estimate of the affine hull, then use it to refine our estimate for ???, then return to this step
ALGORITHM OUTLINE 1. Crudely estimate ??? 2. Crudely estimate affine hull ? of ?? s: ? ?????: ???= 1 3. Refine estimate for ??? 4. Refine estimate for ? hardest part of the analysis 5. Estimate span ?1, ,?? 6. Epsilon-net over span ?1, ,?? to learn ?
ALGORITHM OUTLINE 3. Refine estimate for ??? hardest part of the analysis
USING A CRUDE AFFINE HULL ESTIMATE Say we have a 1/poly ? -accurate estimate ? of the affine hull Idea: Use a representative point ? in ?as a proxy for the actual attention heads ( ? ? ? ???) Wait for an example ?which induces a very high-margin (i.e. nearly 1-sparse) attention pattern in some row of softmax ? ?? Conditioned on this pattern being high-margin, the patterns for the actual attention heads must also be high-margin
USING A CRUDE AFFINE HULL ESTIMATE Say we have a 1/poly ? -accurate estimate ? of the affine hull Idea: Even though ?is only 1/poly ? -close to ?? s, the pattern it induces will be very close to the ones induced by the actual attention heads (e.g. 100,2 and (100000,1) are far, but their softmaxes are ? 98-close) Can use ? and this pattern to read off (very accurate) approximate linear constraint on ??? Repeat until we can solve for a very accurate estimate for ???
TAKEAWAYS Realizable PAC learning as a clean sandbox for probing the learnability of transformers Unlike in the traditional feed-forward setting, our target functions are not multi-index models, and we go beyond Gaussian inputs Techniques do not use rotation invariance or delicate structure of the moments, only concentration and anti-concentration Need to make many niceness assumptions on the target function, interesting open question which ones can be removed Can the theories for learning feed-forward networks and for learning multi-head attention be composed ?
TAKEAWAYS Thanks! Generation by a 21M parameter transformer with only one attention layer, from [Eldan-Li 23] Can the theories for learning feed-forward networks and for learning multi-head attention be composed ?