Understanding Linear Momentum and Collisions in Physics
Exploring the concepts of linear momentum, collisions, and conservation of energy in physics, this content covers topics such as momentum definition, conservation laws, impulse, types of collisions, and examples of perfectly inelastic and elastic collisions. It also includes a practical blackboard example and discusses the principles behind rocket ship propulsion in space.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
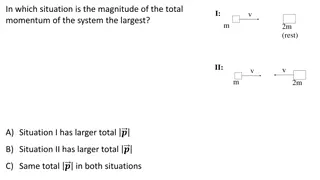
Chapter 9: Linear Momentum and Collisions Reading assignment: Chapter 9.1 to 9.7 Homework 9.1 (due Friday, Oct. 26): QQ1, QQ3, AE1, AE5, 8, 11, 12, 23, 32, 33, 36, 37, 41 Homework 9.2 (due Friday, Oct. 26): 13, 18, 45, 48, 82 = p m v Momentum Momentum is conserved even in collisions with energy loss. Collisions Center of mass Impulse All grades will be continued to be posted on our web page; listed by last four digits of student ID
Chapter 9: Linear Momentum and Collisions The linear momentum of a particle of mass m and velocity v is defined as p = m v The linear momentum is a vector quantity. It s direction is along v. The components of the momentum of a particle: = = = p m v p m v p m v x x y y z z
Conservation of linear momentum = = constant p p or: = p + p i f = + p p p p 1, 2, 1, 2, i i f f
Black board example 9.1 (similar to blocks and spring HW problem) You (100kg) and your skinny friend (50.0 kg) stand face-to- face on a frictionless, frozen pond. You push off each other. You move backwards with a speed of 5.00 m/s. 1. What is the total momentum of the you- and-your-friend system? A. 0 kgm/s B. 250 kgm/s C. 500 kgm/s D. 750 kgm/s E. -500 kgm/s 2. What is your momentum after you pushed off? A. 0 kgm/s B. 250 kgm/s C. 500 kgm/s D. 750 kgm/s E. -500 kgm/s 3. What is your friends speed after you pushed off? A. 0 m/s B. 5 m/s C. 10 m/s D. -5 m/s E. -10m/s 4. How much energy (work) did you and your friend expend? Demo: How are rocket ships (in space) able to change their velocity?
Elastic and inelastic collisions in one dimension Momentum is conserved in any collision, elastic and inelastic. Mechanical Energy is only conserved in elastic collisions. Perfectly inelastic collision: After colliding, particles stick together. There is a loss of kinetic energy (deformation). Elastic collision: Particles bounce off each other without loss of kinetic energy. Inelastic collision: Particles collide with some loss of kinetic energy, but don t stick together.
Perfectly inelastic collision of two particles (Particles stick together) = p p Notice that p and v are vectors and, thus have a direction (+/-) i f + = + ( ) m v m v m m v 1 1 2 K 2 1 2 i i f = E K i loss 1 f There is a loss in energy, Eloss 1 1 2 2 2 + = + + ( ) m v m v m m v E 1 1 2 2 1 2 i i f loss 2 2 2
Perfectly elastic collision of two particles (Particles bounce off each other without loss of energy. Momentum is conserved: + = + m v m v m v m v 1 1 2 2 1 1 2 2 i i f f Energy is conserved: 1 1 1 1 2 2 2 2 + = + m v m v m v m v 1 1 2 2 1 1 2 2 i i f f 2 2 2 2 By plugging one equation into the other, we can also derive: + = + v v v v 1 1 2 2 i f i f
Black board example 9.2 Two carts collide elastically on a frictionless track. The first cart (m1 = 1kg) has a velocity in the positive x-direction of 2 m/s; the other cart (m = 0.5 kg) has velocity in the negative x-direction of 5 m/s. (a) Find the speed of both carts after the collision. (b) Now, what is the speed if the collision is perfectly inelastic? (c) How much energy is lost in the inelastic collision?
Black board example 9.3 and demo Determining the speed of a bullet A bullet (m = 0.01kg) is fired into a block (0.1 kg) sitting at the edge of a table. The block (with the embedded bullet) flies off the table (h = 1.2 m) and lands on the floor 2 m away from the edge of the table. a.) What was the speed of the bullet? b.) What was the energy loss in the bullet-block collision? vb = ? h = 1.2 m x = 2 m
Two-dimensional collisions (Two particles) Conservation of momentum: = = p p i f + + mv m v mv m v 1 1 2 2 1 1 2 2 i i f f Split into components: = = p p , , x i x f + + mv m v mv m v 1 1 2 2 1 1 2 2 ix ix fx fx = = p p , , y i y f + + mv m v mv m v 1 1 2 2 1 1 2 2 iy iy fy fy If the collision is elastic, we can also use conservation of energy.
Black board example 9.4 Accident investigation. Two automobiles of equal mass approach an intersection. One vehicle is traveling towards the east with 29 mi/h (13.0 m/s) and the other is traveling north with unknown speed. The vehicles collide in the intersection and stick together, leaving skid marks at an angle of 55 north of east. The second driver claims he was driving below the speed limit of 35 mi/h (15.6 m/s). a) Is he telling the truth? 13.0 m/s ??? m/s b) What is the speed of the combined vehicles right after the collision? c) How long are the skid marks ( k = 0.5)?
Motion of a System of Particles. Newton s second law for a System of Particles The center of mass of a system of particles (combined mass M) moves like one equivalent particle of mass M would move under the influence of an external force. = F M = a net CM = = F Ma F Ma F Ma , , , , , , net x CM x net y CM y net z CM z
Center of mass m r i i = i r Center of mass for many particles: CM M Black board example 9.5 Where is the center of mass of this arrangement of particles. (m3 = 2 kg; m1 = m2 = 1 kg)? Velocity of the center of mass: Acceleration of the center of mass: m a m v i i i i = = a i v i CM CM M M
A rocket is shot up in the air and explodes. Describe the motion of the center of mass before and after the explosion.
A method for finding the center of mass of any object. - Hang object from two or more points. - Draw extension of suspension line. - Center of mass is at intercept of these lines.
Impulse (change in momentum) = = J p p p A change in momentum is called impulse : f i = = avg p J F t For a constant (average) force: t During a collision, a force F acts on an object, thus causing a change in momentum of the object: f i t = = ( ) p J F t dt Think of hitting a soccer ball: A force F acting over a time t causes a change p in the momentum (velocity) of the ball.
Black board example 9.5 A soccer player hits a ball (mass m = 440 g) coming at him with a velocity of 20 m/s. After it was hit, the ball travels in the opposite direction with a velocity of 30 m/s. 1. What impulse acts on the ball while it is in contact with the foot? 2. The impact time is 0.1s. What average force is the acting on the ball? 3. How much work was done by the foot? (Assume an elastic collision.) 1A. 0 2A. 0 3A. 0 1B. 20 kg m/s 2B. 200 N 3B. 110 J 1C. 22 kg m/s 2C. 220 N 3C. 220 J 1D. 30 kg m/s 2D. 300 N 3D. 300 J 1E. 33 kg m/s 2E. 330 N 3E. 330 J