Understanding Energy Conversion, Power, and Momentum in Physics
Exploring the concepts of energy conversion between potential and kinetic energy, the importance of power in work efficiency, and the role of momentum and impulse in describing motion in physics. The discussion covers elastic forces, work done, power calculations, examples of watt and joules, as well as a quiz on energy conservation. Additionally, it delves into momentum, collisions, and the conservation of momentum in various scenarios.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
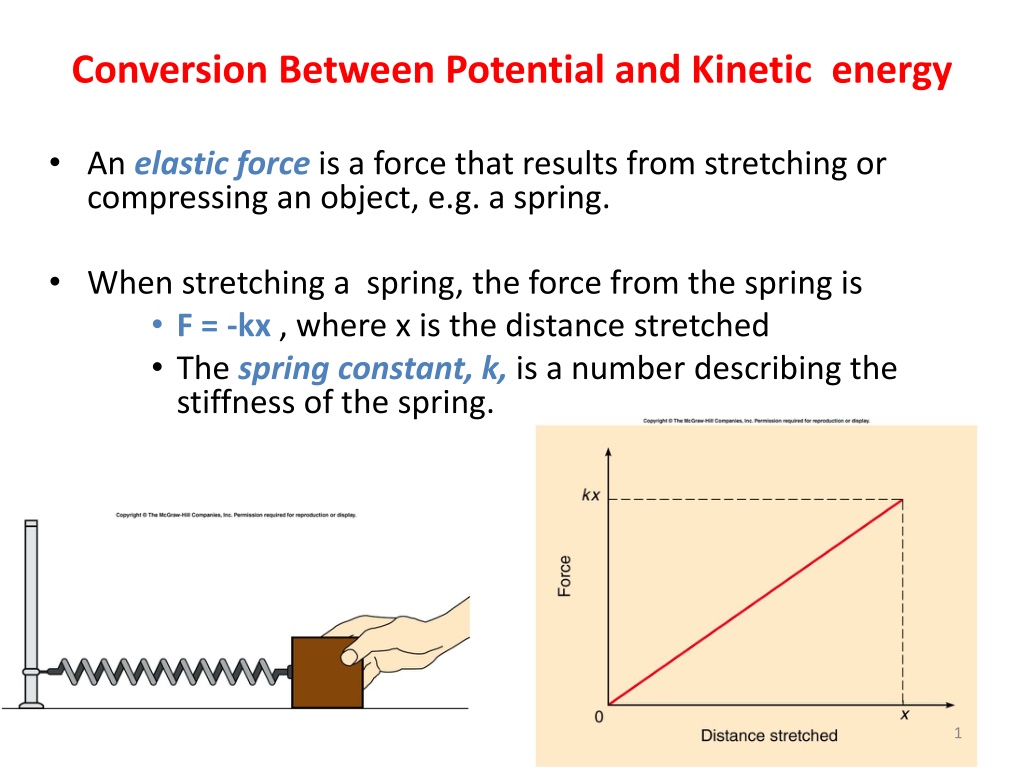
Conversion Between Potential and Kinetic energy An elastic force is a force that results from stretching or compressing an object, e.g. a spring. When stretching a spring, the force from the spring is F = -kx , where x is the distance stretched The spring constant, k, is a number describing the stiffness of the spring. 1
Conversion Between Potential and Kinetic energy The increase in elastic potential energy is equal to the work done by the average force needed to stretch the spring. = distance average = done work force PE 1 = 2 PE kx 2 3
Power It is not only important how much work is done but also how quick, i.e. the rate, at which work is done So the quantity Power = P = W/t (unit is a watt) is very important. Generally energy supplies, motors, etc are rated by power and one can determine how much work can be done by multiplying by time. W = Pt (joules). 9/29/2024 4 4
Examples of Watt and Joules The unit for electrical usage is the kilowatt hour. A kilowatt hour is the energy used by a 1000 watt device for 3600 seconds 1kWHr = 1000*3600 = 3.6 million joules In order to lift an elevator with a mass of 1000kg to 100 meters requires 1000*9.8*100 joules but we need to do it in 20 seconds. The power we need is 1000*9.8*100/20 = 49000 Watts so we need to install a motor rated at > 49000 watts 5
Quiz: A sled and rider with a total mass of 40 kg are perched at the top of the hill shown. Suppose that 2000 J of work is done against friction as the sled travels from the top (at 40 m) to the second hump (at 30 m). Will the sled make it to the top of the second hump if no kinetic energy is given to the sled at the start of its motion? a) b) c) yes no It depends. Energy conservation: mgH = mgh + KE + heat 40kg X 9.8N/s2 X 40m = 40kg X 9.8N/s2 X 30m + KE + 2000J KE = 1920 J > 0, i.e. yes, he can reach the 2nd hump. 6
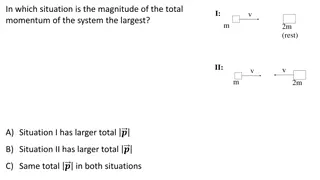
Momentum and Impulse How can we describe the change in velocities of colliding football players, or balls colliding with bats? How does a strong force applied for a very short time affect the motion? Can we apply Newton s Laws to collisions? What exactly is momentum? How is it different from force or energy? What does Conservation of Momentum mean? 7
What happens when a ball bounces? When it reaches the floor, its velocity quickly changes direction. There must be a strong force exerted on the ball by the floor during the short time they are in contact. This force provides the upward acceleration necessary to change the direction of the ball s velocity. Fnet= ma = m v t 8
Momentum and Impulse Fnet= ma = m v Multiply both sides of Newton s second law by the time interval over which the force acts: t The left side of the equation is impulse, the (average) force acting on an object multiplied by the time interval over which the force acts. Fnet t = m v How a force changes the motion of an object depends on both the size of the force and how long the force acts. The right side of the equation is the change in the momentum of the object. The momentum of the object is the mass of the object times its velocity. p = mv 9
Impulse-Momentum Principle The impulse acting on an object produces a change in momentum of the object that is equal in both magnitude and direction to the impulse. impulse = change in momentum v F = m t net = p When F = 0, p = 0, i.e. total momentum has no change as a function of time, i.e. conserved 10
Conservation of Momentum p = F t This is the impulse equation When F = 0, p = 0, i.e. total momentum has no change as a function of time, i.e. conserved 11
Does the momentum of the fullback conserve? A). Yes, because the external force is zero. B). No, because the external force is NOT zero 12
Does the sum of the momentum of the two players conserve? A). Yes, because the external force is zero. B). No, because the external force is NOT zero 13
Conservation of Momentum Newton s third law For every action, there is an equal but opposite reaction. The defensive back exerts a force on the fullback, and the fullback exerts an equal but opposite force on the defensive back. The impulses on both are equal and opposite. The changes in momentum for each are equal and opposite. The total change of the momentum for the two players is zero. 14
Conservation of Momentum For any system, if the net external force acting on a system of objects is zero, the total momentum of the system is conserved. p = F t F = 0, p = 0 15
A 100-kg fullback moving straight downfield collides with a 75-kg defensive back. The defensive back hangs on to the fullback, and the two players move together after the collision. What is the initial momentum of each player? A). Full back: 500 kg m/s2, defensive back: -300 kg m/s2 B). Full back: 500 kg m/s2, defensive back: 300 kg m/s2 C). Full back: 200 kg m/s2, defensive back: -300 kg m/s2 D). Full back: 250 kg m/s2, defensive back: 300 kg m/s2 p = mv = (100 kg) (5 m/s) = 500 kg m/s2 p = mv = (75 kg)(-4 m/s)= -300 kg m/s2 Fullback: 16 Defensive back:
What is the total momentum of the system? A). 150 kg m/s2 B). 500 kg m/s2 C). 100 kg m/s2 D). 200 kg m/s2 Total momentum: ptotal = pfullback + pdefensive back = 500 kg m/s - 300 kg m/s = 200 kg m/s 17
What is the velocity of the two players immediately after the collision? Total mass: m = 100 kg + 75 kg = 175 kg A. 4.5m/s B. 1.14m/s C. 153 m/s Velocity of both: v = ptotal / m = (200 kg m/s) / 175 kg = 1.14 m/s D. 0 m/s E. 0.25m/s 18
Two skaters of different masses prepare to push off against one another. Which one will gain the larger velocity? a) b) c) The more massive one The less massive one They will each have equal but opposite velocities. The net external force acting on the system is zero, so conservation of momentum applies. Before the push-off, the total initial momentum is zero. The total momentum after the push-off should also be zero. Both must move with momentum values equal in magnitude but opposite in direction: p2 = p1 When added together, the total final momentum of the system is then zero. Since momentum is mass times velocity p = mv, the skater with the smaller mass must have the larger velocity: m1v1 = m2v2 19
Recoil The explosion of the powder causes the shot to move very rapidly forward. If the gun is free to move, it will recoil backward with a momentum equal in magnitude to the momentum of the shot. 20
Even though the mass of the shot is small, its momentum is large due to its large velocity. The shotgun recoils with a momentum equal in magnitude to the momentum of the shot. The recoil velocity of the shotgun will be smaller than the shot s velocity because the shotgun has more mass, but it can still be sizeable. 21
How can you avoid a bruised shoulder? If the shotgun is held firmly against your shoulder, it doesn t hurt as much. WHY? 22
Elastic and Inelastic Collisions Different kinds of collisions produce different results. Sometimes the objects stick together. Sometimes the objects bounce apart. What is the difference between these types of collisions? Is energy conserved as well as momentum? 23
A ball bouncing off a floor or wall with no decrease in the magnitude of its velocity is an elastic collision. The kinetic energy does not decrease. No energy has been lost. A ball sticking to the wall is a perfectly inelastic collision. The velocity of the ball after the collision is zero. Its kinetic energy is then zero. All of the kinetic energy has been lost. Does the total momentum become zero? Most collisions involve some energy loss, even if the objects do not stick, because the collisions are not perfectly elastic. Heat is generated, the objects may be deformed, and sound waves are created. These would be partially inelastic collisions. 24
Four railroad cars, all with the same mass of 20,000 kg, sit on a track. A fifth car of identical mass approaches them with a velocity of 15 m/s. This car collides and couples with the other four cars. What is the initial momentum of the system? m5 v5 pinitial = 20,000 kg = 15 m/s = m5v5 = (20,000 kg)(15 m/s) = 300,000 kg m/s 200,000 kg m/s 300,000 kg m/s 600,000 kg m/s 1,200,000 kg m/s a) b) c) d) 25
What is the velocity of the five coupled cars after the collision? 1 m/s 3 m/s 5 m/s 10 m/s mtotal pfinal vfinal = 100,000 kg = pinitial = pfinal / mtotal = (300,000 kg m/s)/(100,000 kg) = 3 m/s a) b) c) d) 26
Is the kinetic energy after the railroad cars collide equal to the original kinetic energy of car 5? KEinitial= 1/2 m5 v52 = 1/2 (20,000 kg)(15 m/s)2 = 2250 kJ KEfinal = 1/2 mtotal vfinal2 = 1/2 (100,000 kg)(3 m/s)2 = 450 kJ KEfinal KEinitial yes no It depends. a) b) c) 27
Quiz: When a ball bounces back with the same speed, the momentum changes from mv to -mv, so the impulse and the change in momentum are A. 2mv, 2mv B. mv, mv C. No change in momentum. Impulse is 0. D. No change in momentum. Impulse is mv 28