Understanding Histograms: Ratios, Rates & Statistics
Explore the world of histograms to analyze data sets efficiently. Learn how to interpret dot plots, find mean, median, and mode, and create histograms. Understand key terms like frequency tables and intervals. Practice identifying the range of data, calculating mean values, and reading histograms effectively. Gain insights into organizing data visually and drawing meaningful conclusions through histograms.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
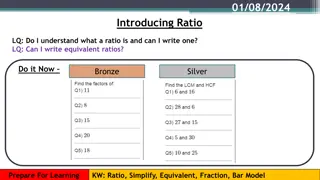
Lesson 4.4 Core Focus on Ratios, Rates & Statistics Histograms
Warm-Up Vicente asked some of his friends about the number of hours they spent doing chores each week. Use the dot plot to answer the following questions. 1. How many friends did Vicente survey? 10 2. What was the range of the data? 6 3. Find the mean, median and mode of the data. Mean = 2.4; Median = 2; Mode = 2
Lesson 4.4 Histograms Make, read and interpret histograms.
Vocabulary Histogram A bar graph in which data values are organized into equal intervals. Histograms display data in the form of numbers whereas bar graphs display data in categories. Good to Know! Each interval on a histogram includes the number on the left-hand side of an interval up to the number on the right- hand side. Frequency Table A table which shows a tally of how many times a value occurred in each interval.
Example 1 Use the histogram to answer each question. a. How many students had 2 or 3 pets? Ten students have 2 or 3 pets. Look at the height (number of students) of the bar that is between 2 and 4.
Example 1 Continued Use the histogram to answer each question. b. How many students had at least 8 pets? There are 3 students who have at least 8 pets. Adding the bars to the right of 8 on the horizontal axis (1 + 2) totals 3.
Example 1 Continued Use the histogram to answer each question. c. The interval between 6 8 is empty. What does that mean? This means that there are 0 students who had exactly 6 or 7 pets.
Example 1 Continued Use the histogram to answer each question. d. How many students are in Ms. Sanchez class? Add the heights of all the bars together. 13 + 10 + 5 + 0 + 1 + 2 = 31 students This sum represents the number of students in the class.
Making A Histogram 1. Identify the minimum and maximum numbers in the data set. 2. Choose an appropriate interval width. Histograms usually have 4 to 12 intervals. 3. Make a frequency table. Tally the number of times a value occurs in each interval. 4. Place the intervals from the frequency table along the horizontal axis of the graph. 5. Create bars for each interval. The height of each bar should equal the number of tally marks in each interval in the frequency table.
Good to Know! Any interval width works for histograms. However, it is ideal to have between 4 and 12 intervals to best display the distribution of data in a histogram. Too many bars will spread the data out so the bars will have very little height. Too few intervals in a histogram will not show the distribution in the graph well.
Example 2 Make a histogram for students pulse rates (in beats per minute) listed below. 64, 76, 60, 70, 68, 70, 88, 62, 54, 68, 70, 72, 60, 92, 64, 76, 70, 68, 62, 72 Minimum = 54 Maximum = 92 Identify the minimum and maximum values. The frequency table must start low enough to include 54 and must go high enough to include 92. The overall range of the data is 92 54 or 38. Determine an appropriate interval width. 38 8 5 An interval width of 5 will create about 8 bars.
Example 2 Continued Make a histogram for students pulse rates (in beats per minute) listed below. 64, 76, 60, 70, 68, 70, 88, 62, 54, 68, 70, 72, 60, 92, 64, 76, 70, 68, 62, 72 Complete the frequency table for the data. When a number in the data set lies on the border of two intervals, put it in the uppermost interval.
Example 2 Continued Make a histogram for students pulse rates (in beats per minute) listed below. 64, 76, 60, 70, 68, 70, 88, 62, 54, 68, 70, 72, 60, 92, 64, 76, 70, 68, 62, 72 Use the information collected in the frequency table to draw the histogram. There were 20 students pulse rates. The heights of the bars sum to 20.
Communication Prompt Give an example of real-world data that could be displayed in a bar graph. Give an example of real- world data that could be displayed in a histogram.
Exit Problems Use the histogram to answer the following questions. 1. What is the interval width? 6 2. Which interval has the most values? 12 18 3. How many values are in the data set? 13 4. How many values are 18 or higher? 5 5. In which interval would the number 12 be included? 12 18