Understanding Ratios with Practical Examples
Ratios describe the relationship between quantities and can be visualized as parts of a whole. Explore equivalent ratios, sharing quantities based on ratios, and solving scenarios involving ratios with examples. Learn how to find missing values in ratios and apply ratio concepts in real-life situations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
RATIO Ratio says how much of one thing there is compared to another
RATIO Ratio tells us how many equal parts of a whole one thing has compared to another The ratio 3:2 can be expressed visually as: You can see there are 5 parts altogether Equal sizes
RATIO You can find equivalent ratio: 3:2 = 6:4 = 9: 6
Equivalent Ratio On whiteboards, show me any equivalent ratio to: 42:35 1:4 5:3 3:2 12:4 3:5 7:1.5
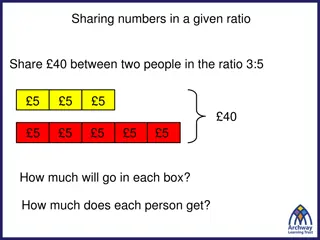
Sharing ratio into a given quantity Share 20 into the ratio 3:2 1 part is 4 So ratio is 12: 8 20 4 4 4 4 4
Your turn Share 21 into the ratio 3:4 Share 121 into the ratio 4:7 Share 36 into the ratio 3.5: 2.5 Share 12.50 into the ratio 2:3 Share 44.25 into the ratio 1:2 9: 12 44: 77 21: 15 5: 7.50 14.75: 29.50
Scott and Megan share some money in the ratio 3:2. Scott gets 12. How much does Megan get? 1 part is 4 12 So Megan gets 2 x 4 = 8
The ratio of the number of Caras CDs to the number of Tahlia s CDs is 3:5. If Tahlia has 45 CDs, how many does Cara have? 1 part is 9 CDs 45 So Cara has 3 x 9= 27 CDs
Your turn Aidan and Matt have football stickers in the ratio 2:3. Altogether they have 25 stickers. If Aidan gives half his stickers to Matt, how many will Matt have? 25 5 5 5 5 5 Aidan Matt
Your turn Aidan and Matt have football stickers in the ratio 2:3. Altogether they have 25 stickers. If Aidan gives half his stickers to Matt, how many will Matt have? 5 5 5 5 5 5 Matt Aidan Matt now has 20 CDs
The ratio of Brooks pencils to Beths pencils was 7:3. When Brook gave 20 pencils to Beth, they each had the same amount. How many pencils did they have altogether?
The ratio of Brooks pencils to Beths pencils was 7:3. When Brook gave 20 pencils to Beth, they each had the same amount. How many pencils did they have altogether? Brook 10 blocks altogether. 20 Beth Brook Still have 10 blocks but same amount each Beth So one block = 10 pencils 10 blocks = 100 pencils
Solving more complicated Ratio problems . The ratio of books owned by Scott and Matthew is 3:5. If Scott gives Matthew 2 of his books, then the ratio will be 1:3 How many books do they each have initially?
The ratio of books owned by Scott and Matthew is 3:5. If Scott gives Matthew 2 of his books, then the ratio will be 1:3 How many books do they each have initially? Scott Matthew We can see that if we move two of the blocks from Scott, to Matthew, the new ratio isn t going to be 1:3, but 1:7
The ratio of books owned by Scott and Matthew is 3:5. If Scott gives Matthew 2 of his books, then the ratio will be 1:3 How many books do they each have initially? Let s look for some equivalent ratios starting by doubling Scott Matthew ..however, ratio shows the comparison of two quantities, so could be in simplified version 3:5 = 6:10
The ratio of books owned by Scott and Matthew is 3:5. If Scott gives Matthew 2 of his books, then the ratio will be 1:3 How many books do they each have initially? Scott Matthew We can now see that if we take 2 books away from Scott and give them to Matthew, our new ratio would be 4:12 = 1:3
The ratio of books owned by Scott and Matthew is 3:5. If Scott gives Matthew 2 of his books, then the ratio will be 1:3 How many books do they each have initially? Scott Matthew So the initial amount of books they each had was 6 for Scott and 10 for Matthew
Jess and Faye own a number of marbles that are in the ratio 5:6. Jess gains 2 more marbles and the ratio is now 7:8. How many marbles did they own originally? 2 11 parts + 2 = 13 divisions. 13 divisions cannot be split into 15 parts so we must look for equivalent ratios of 5:6
Jess and Faye own a number of marbles that are in the ratio 5:6. Jess gains 2 more marbles and the ratio is now 7:8. How many marbles did they own originally? 2 5:6 = 10:12 22 parts + 2 = 24 divisions which cannot be split into 15 parts
Jess and Faye own a number of marbles that are in the ratio 5:6. Jess gains 2 more marbles and the ratio is now 7:8. How many marbles did they own originally? 2 5:6 = 40:48 88 parts + 2 = 90 divisions which can be split into 15 parts
Jess and Faye own a number of marbles that are in the ratio 5:6. Jess gains 2 more marbles and the ratio is now 7:8. How many marbles did they own originally? 2 So, originally, Jess had 40 marbles and Faye had 48
Jess and Faye own a number of marbles that are in the ratio 5:6. Jess gains 2 more marbles and the ratio is now 7:8. How many marbles did they own originally? Hint 1: equivalent ratios... Hint 2: you ll need an equivalent ratio of 5:6 that if you add 2 to the 5 equivalent, will generate a ratio that can be SIMPLIFIED to a ratio of 7:8 . Hint 3: your second ratio will have to be a multiple of 8 so find the LCM of both 6 and 8 as these are the two parts that won t change
Jess and Faye own a number of marbles that are in the ratio 5:6. Jess gains 2 more marbles and the ratio is now 7:8. How many marbles did they own originally? We could continue looking for equivalent ratio that will generate the correct simplification in this way, or we could try to reduce our workload by thinking about LCMs 5:6 = 10:12 7: 6 Add 2 to Jess 12:12
Jess and Faye own a number of marbles that are in the ratio 5:6. Jess gains 2 more marbles and the ratio is now 7:8. How many marbles did they own originally? Faye s marbles are going to have to simplify to 8 so we actually need to find a multiple of 6 that is also a multiple of 8 .. 5:6 = 40:48 Add 2 to Jess 42:48 7:8 SIMPLIFY The LCM of 6 and 8 is 48
The ratio of cockles to winkles in a bag of seashells is 1:2 When 6 winkles are accidentally spilt from the bag, the ratio is 3:5 How many of each shell were there originally?
The ratio of Anns age to Bobs age is 3:4. In 7 years time, this ratio will be 4:5 i. what are their ages now? ii. after how many years from now will the ratio be 5:6?