Understanding Heterogeneous Catalytic Reactions: Steps and Mechanisms
The content discusses the key steps involved in a heterogeneous catalytic reaction, focusing on diffusion, mass transfer, adsorption, desorption, and surface reactions. It highlights the importance of considering external diffusion effects and provides guidelines for deducing reaction mechanisms in such systems. The role of diffusion, both external and internal, is explored in determining the overall reaction rate, emphasizing the significance of mass transfer limitations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
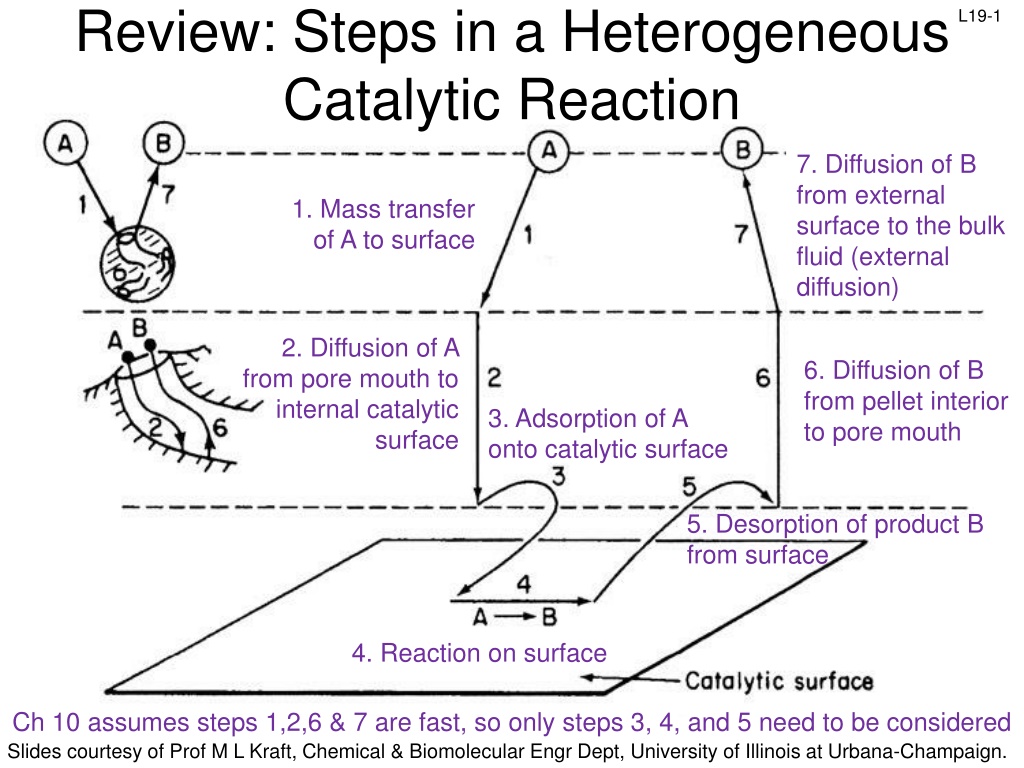
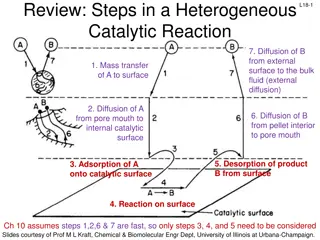
Review: Steps in a Heterogeneous Catalytic Reaction L19-1 7. Diffusion of B from external surface to the bulk fluid (external diffusion) 1. Mass transfer of A to surface 2. Diffusion of A from pore mouth to internal catalytic 6. Diffusion of B from pellet interior to pore mouth 3. Adsorption of A onto catalytic surface surface 5. Desorption of product B from surface 4. Reaction on surface Ch 10 assumes steps 1,2,6 & 7 are fast, so only steps 3, 4, and 5 need to be considered Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
Review: Guidelines for Deducing Mechanisms L19-2 More than 70% of heterogeneous reaction mechanisms are surface reaction limited When you need to propose a rate limiting step, start with a surface reaction limited mechanism unless you are told otherwise If a species appears in the numerator of the rate law, it is probably a reactant If a species appears in the denominator of the rate law, it is probably adsorbed in the surface + i j k kPP K P + i j = Generic equation: r' A 1 KP + + K P i i j j k k Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-3 L19: External Diffusion Effects Up until now we have assumed adsorption, surface reaction, or desorption was rate limiting, which means there are no diffusion limitations In actuality, for many industrial reactions, the overall reaction rate is limited by the rate of mass transfer of products and reactants between the bulk fluid and the catalyst surface External diffusion (today) Internal diffusion (L20, L21 & L21b) Goal: Overall rate law for heterogeneous catalyst with external diffusion limitations. This new overall reaction rate would be inserted into the design equation to get W, XA, CA, etc External diffusion Internal diffusion Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-4 Mass Transfer Diffusion: spontaneous intermingling or mixing of atoms or molecules by random thermal motion External diffusion: diffusion of the reactants or products between bulk fluid and external surface of the catalyst Molar flux (W) Molecules of a given species within a single phase will always diffuse from regions of higher concentrations to regions of lower concentrations This gradient results in a molar flux of the species, (e.g., A), WA (moles/area time), in the direction of the concentration gradient A vector: W W = + W i j + W k A Ax Ay Az Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-5 Molar Flux W & Bulk Motion BA Molar flux consists of two parts Bulk motion of the fluid, BA Molecular diffusion flux relative to the bulk motion of the fluid produced by a concentration gradient, JA WA = BA + JA (total flux = bulk motion + diffusion) Bulk flow term for species A, BA: total flux of all molecules relative to fixed coordinates ( Wi) times the mole fraction of A (yA): = B Or, expressed in terms of concentration of A & the molar average velocity V: y W A A i mol m mol m m = = = C C y B V B i i V A A A A 2 3 s s The total molar flux of A in a binary system composed of A & B is then: C C y y = + + W J W W = = + + In terms of concentration of A W W J J V A A A i i V A A A ( ) In terms of mol fraction A A A A A B Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-6 Diffusional Flux of A, JA & Molar Flux W WA = JA + BA (total flux = diffusion + bulk motion) = = = + + + C C y W W W J J J V A A A W y i i V A A A ( ) + W A A A A B Diffusional flux of A resulting from a concentration difference, JA, is related to the concentration gradient by Fick s first law: mol m s = cD y J A AB A 2 c: total concentration DAB: diffusivity of A in B yA: mole fraction of A = + + i j k gradient in rectangular coordinates x y z Putting it all together: = + cD y y W W General equation A AB A A i i ( ) = + + cD y y W W W molar flux of A in binary system of A & B A AB A A A B Effective diffusivity, DAe: diffusivity of A though multiple species Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-7 Simplifications for Molar Flux WA = JA + BA (total flux = diffusion + bulk motion) = + cD y y W W General equation: A AB A A i i ( ) = + + cD y y W W W A AB A A A B Molar flux of A in binary system of A & B For constant total concentration: cDAByA = DABCA When there is no bulk flow: = W 0 i i y W 0 For dilute concentrations, yA is so small that: A i i For example, consider 1M of a solute diffusing in water, where the concentration of water is 55.6 mol water/dm3 C 1 y C C 1 55.6 + + A = = = y 0.018 0 A A A W Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-8 Evaluation of Molar Flux Type 1: Equimolar counter diffusion (EMCD) For every mole of A that diffuses in a given direction, one mole of B diffuses in the opposite direction Fluxes of A and B are equal in magnitude & flow counter to each other: WA = - WB A AB A cD y = or for constant total concentration: A AB A cD y = Type 2: Dilute concentration of A: ( ) A AB A A A B cD y y = + + W W W W W W 0 Type 3: Diffusion of A though stagnant B: WB=0 ( A AB A A A cD y y = + + W W W W W W ( ) W W W W W W + + y A A B 0 bulk motion 0 W W W W = D C A AB A y W 0 A i i W W or constant C = W W : = cD y total C A AB A D A AB A 1 ) W W = cD y A AB A B 1 y 0 A Type 4: Forced convection drives the flux of A. Diffusion in the direction of flow (JA) is tiny compared to the bulk flow of A in that direction (z): volumetric flow rate W W = W W V V W W C = + 0 diffusion 0 = cD y C C A z V A A A AB A A z A A c cross-sectional area Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-9 Boundary Conditions Boundary layer Hydrodynamics boundary layer thickness: distance from a solid object to where the fluid velocity is 99% of the bulk velocity U0 Mass transfer layer thickness: distance from a solid object to where the concentration of the diffusing species is 99% of the bulk concentration Typically diffusive transport is modelled by treating the fluid layer next to a solid boundary as a stagnant film of thickness CAb CAs CAs: Concentration of A at surface CAb: Concentration of A in bulk In order to solve a design equation that accounts for external diffusion limitations we need to set the boundary conditions Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-10 Types of Boundary Conditions Concentration at the boundary (i.e., catalyst particle surface) is specified: If a specific reactant concentration is maintained or measured at the surface, use the specified concentration When an instantaneous reaction occurs at the boundary, then CAs 0 Flux at the boundary (i.e., catalyst particle surface) is specified: a) No mass transfer at surface (nonreacting surface) W 1. 2. = 0 Asurface b) Reaction that occurs at the surface is at steady state: set the molar flux on the surface equal to the rate of reaction at the surface W r '' = reaction rate per unit surface area (mol/m2 sec) A A surface c) Convective transport across the boundary layer occurs W ( ) = k C C A c Ab As boundary 3. Planes of symmetry: concentration profile is symmetric about a plane Concentration gradient is zero at the plane of symmetry dC dr Radial diffusion in a tube: Radial diffusion in a sphere A = 0 at r=0 r r Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-11 Correlation for Convective Transport Across the Boundary Layer For convective transport across the boundary layer, the boundary condition is: ( ) = W k C C A c Ab As boundary The mass transfer coefficient for a single spherical particle is calculated from the Fr ssling correlation: c k d D AB = Sh p kc: mass transfer coefficient dp: diameter of pellet (m) DAB: diffusivity (m2/s) Sh: Sherwood number (dimensionless) 12 13 = 2 0.6Re + Sh Sc Ud = p Schmidt number: Sc Reynold's number Re= D AB : kinematic viscosity or momentum diffusivity (m2/s); = : fluid density (kg/m3) U: free-stream velocity (m/s) DAB: diffusivity (m2/s) : viscosity (kg/m s) dp: diameter of pellet (m) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-12 Rapid Rxn on Catalyst Surface Spherical catalyst particle in PBR Liquid velocity past particle U = 0.1 m/s Catalyst diameter dp= 1 cm = 0.01 m Instantaneous rxn at catalyst surface CAs 0 Bulk concentration CAb= 1 mol/L kinematic viscosity = 0.5 x 10-6 m2/s DAB = 1x10-10 m2/s The velocity is non-zero, so we primarily have convective mass transfer to the catalyst particle: A boundary Compute kC from Fr ssling correlation: ( ) 6 2 0.5 10 m s ( ) ( 200 Sh 2 .6 0 0 + = 1 0 2 1 10 m 0.01 m CAb= 1 mol/L 0.01m CAs=0 Determine the flux of A to the catalyst particle ( ) = W k cC C Ab As D Re=Ud AB d p = k S h = Sc 1 2 13 = + Sh 2 0.6 Re Sc c D p AB 6 2 0.1m s 0.01m 0.5 10 1 10 ) 00 m m s = Sc 5000 = = Sc = Re Re 2000 10 2 s 1 2 13 = Sh 461 50 m s s 6 = k 4.61 10 = k 461 c c Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-13 Rapid Rxn on Catalyst Surface Spherical catalyst particle in PBR Liquid velocity past particle U = 0.1 m/s Catalyst diameter dp= 1cm = 0.01m Instantaneous rxn at catalyst surface CAs 0 Bulk concentration CAb= 1 mol/L kinematic viscosity = 0.5 x 10-6 m2/s DAB = 1x10-10 m2/s The velocity is non-zero, so we primarily have convective mass transfer to the catalyst particle: Aboundary Computed kC from Fr ssling correlation: CAb= 1 mol/L 0.01m CAs=0 Determine the flux of A to the catalyst particle ( ) = W k C C c D A b A s m s 6 AB d = k Sh = k 4.61 10 c c p mol m m s mo 1000L l 1 L 3 0 6 = = W 4.61 10 W 4.61 1 0 Aboundary Abound ary 2 3 s m Because the reactant is consumed as soon as it reaches the surface mol m 3 = = W As r '' 4.61 10 A boundary 2 s Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-14 For the previous example, derive an equation for the flux if the reaction were not instantaneous, and was instead at steady state (WA|surface =-rA ) and followed the kinetics: -rAS =krCAs (Observed rate is not diffusion limited) ( ) c Ab As Aboundary = k C C W As r = '' k C r As Because the reaction at the surface is at the steady state & not instantaneous: C 0 = = W As r '' rk C A As boundary As So if CAs were in terms of measurable species, we would know WA,boundary Use the equality to put CAs in terms of measurable species (solve for CAs) ( ) = + = = k C k rC k C k C k cC k C k C C k C c A b A s c As c A b A s r As c Ab As r A s k C k c Ab k ( ) = C Plug into -r As = + k C C k k As c Ab A s r c + r c k k C k Diffusion limited r c + Ab k r'' = = W r'' = = W r'' k C A As A As r A k k C k k k C k s boundary bounda y r r c r c k k C Rapid rxn, kr>>kc kc in denominator is negligible = k C r c Ab k Ab = = r'' r'' As c Ab As As + k r c r r c k k C Slow rxn, kr<<kc kr in denominator is negligible Reaction limited = r'' k C r c Ab k Ab = = r'' r'' As r Ab As As + k r c c Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-15 Mass Transfer & Rxn Limited Reactions r c k k C k Ab k reaction limited regime r'' = = r'' As + k C r c As r Ab transport limited regime r'' k C = -rA As c Ab D Ud AB d = p k Sh = Sc 12 13 Re= = 2 0.6Re + Sh Sc c D p AB 1 2 13 Ud D p AB d = + k 2 0.6 c D p AB (U/dp)1/2 (fluid velocity/particle diameter)1/2 When measuring rates in the lab, use high velocities or small particles to ensure the reaction is not mass transfer limited Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-16 Mass Transfer & Rxn Limited Reactions r c k k C k Ab k reaction limited regime r'' = = r'' As + k C r c As r Ab transport limited regime r'' k C = -rA As c Ab D Ud AB d = p k Sh = Sc 12 13 Re= = 2 0.6Re + Sh Sc c D p AB 1 2 13 Ud D p AB d = + k 2 0.6 c D p AB (U/dp)1/2 = (fluid velocity/particle diameter)1/2 k k Proportionality is useful for assessing parameter sensitivity 1 2 1 2 2 3 1 6 2 3 1 2 d d D U U D U p1 AB 1 6 c2 2 AB2 D 1 = k c 1 2 p d c1 1 AB1 2 p2 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-17 Mass Transfer Limited Rxn in PBR b a c a d a + + A B C D A steady state mole balance on reactant A between z and z + z : ( ) 6 1 + = = Az z F Az z F r'' a (A z) 0 where a + z A c c c d p ac: external surface area of catalyst per volume of catalytic bed (m2/m3) : porosity of bed, void fraction r A: rate of generation of A per unit catalytic surface area (mol/s m2) Divide out Ac z: c A z Put Faz and rA in terms of CA: Axial diffusion is negligible compared to bulk flow (convection) F B A UC A = = z z Substitute into the mass balance ( ) A A c r'' a 0 dz dz dp: particle diameter (m) dF dz 1 Az z F Az z F Take limit as z 0: W = z Az + = + r'' a 0 z + = r'' a 0 A c A c A = c + F A (J B )A A A c A A c z z z A A c A c dC dz dC dU dz d UC 0 A A + = + + = U r'' a 0 U C r'' a 0 + = A c A A c Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-18 Mass Transfer Limited Rxn in PBR b a c a d a dC dz A + + + = A B C D U r'' a 0 A c At steady-state: Molar flux of A to particle surface = rate of disappearance of A on the surface r'' W = = mass transfer coefficient kc =DAB/ (s-1) boundary layer thickness CAs: concentration of A at surface ( ) c c A As U k a C C 0 dz dC U k a C 0 dz varies with distance down reactor dC U k a C dz A C A0 k a C exp z C U ( ) k C C Substitute A Ar c A As CA: concentration of A in bulk dC A = CAs 0 in most mass transfer-limited rxns Rearrange & integrate to find how CA and the r A A = c c A C c c k a U C C z c c k a U dC C A A = A A ln z = = dz c c A A0 0 c c k a U c c k a U c c A = = = C C exp z r'' k C exp z A A0 A c A0 A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-19 Review: Heterogeneous Catalyst We have looked at cases where 1) Adsorption, surface reaction, or desorption is rate limiting 2) External diffusion is rate limiting 3) Internal diffusion is rate limiting- today Next time: Derive an overall rate law for heterogeneous catalyst where the rate limiting step as any of the 7 reaction steps. This new overall reaction rate would be inserted into the design equation to get W, XA, CA, etc Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-20 Review: Types of Boundary Conditions 1. Concentration at the boundary (i.e., catalyst particle surface) is specified: If a specific reactant concentration is maintained or measured at the surface, use the specified concentration When an instantaneous reaction occurs at the boundary, then CAs 0 2. Flux at the boundary (i.e., catalyst particle surface) is specified: a) No mass transfer at surface (nonreacting surface) W = 0 Asurface b) Reaction that occurs at the surface is at steady state: set the molar flux on the surface equal to the rate of reaction at the surface W r '' = reaction rate per unit surface area (mol/m2 sec) A A surface c) Convective transport across the boundary layer occurs W ( ) = k C C A c Ab As boundary 3. Planes of symmetry: concentration profile is symmetric about a plane Concentration gradient is zero at the plane of symmetry dC dr Radial diffusion in a tube: Radial diffusion in a sphere A = 0 at r=0 r r Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-21 Review: Transport & Rxn Limited Rates reaction limited regime: Used kc(CAb-CAs)=krCAS to solve for CAs & plugged back into r As= krCAS = r'' k C As r Ab k k C k r c Ab k = r '' As + r c transport limited regime (Convective transport across boundary layer) = As c Ab r'' k C AB c p d Ud D 2 0.6 d -rA D Ud p = = k Sh Sc 12 13 Re= = 2 0.6Re + Sh Sc D AB 1 2 13 p AB = + k c D p AB (U/dp)1/2 (fluid velocity/particle diameter)1/2 When measuring rates in the lab, use high velocities or small particles to ensure the reaction is not mass transfer limited Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
Review: Mass Transfer Limited Rxn in PBR L19-22 b a c a d a + + A B C D A steady state mole balance on reactant A between z and z + z : ( ) 6 1 + = = Az z F Az z F r'' a (A z) 0 where a + z A c c c d p ac: external surface area of catalyst per volume of catalytic bed (m2/m3) : porosity of bed, void fraction r A: rate of generation of A per unit catalytic surface area (mol/s m2) Ac: cross-sectional area of tube containing catalyst (m2) Divide out Ac z and take limit as z 0 Put Faz and rA in terms of CA Assume that axial diffusion is negligible compared to bulk flow Assume molar flux of A to surface = rate of consumption of A at surface Rearrange, integrate, and solve for CA and r A k a C C exp z U dp: particle diameter (m) 1. 2. 3. 4. 5. c c k a U c c = = r'' k C exp z A A0 A c A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-23 Shrinking Core Model Solid particles are being consumed either by dissolution or reaction The amount of the material being consumed is shrinking Drug delivery (pill in stomach) Catalyst regeneration Regeneration of catalyst by burning off carbon coke in the presence of O2 Begins at the surface and proceeds to the core Because the amount of carbon that is consumed (burnt off) is proportional to the surface area, and the amount of carbon that is consumed decreases with time Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-24 Catalyst Regeneration Coking-deactivated catalyst particles are reactivated by burning off the carbon + C O CO 2 2 R0 Oxygen (A) diffuses from particle surface (r = R0,CA = CA0) through the porous pellet matrix to the unreacted core (r = R, CA = 0) Reaction of O2 with carbon at the surface of the unreacted core is very fast CO2 generated at surface of core diffuses out Rate of oxygen diffusion from the surface of the pellet to the core controls rate of carbon removal O2 r+ r r R CO2 r : radius R0:outer radius of particle R: radius of unreacted core r = 0 at core What is the rate of time required for the core to shrink to a radius R? Though the core of carbon (from r = 0 to r = R0) is shrinking with time (unsteady state), we will assume the concentration profile at any time is the steady state profile over distance (R0- R): quasi-steady state assumption (QSSA) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-25 Mole Balance on O2 From r to r+ r + Rate in - rate out + gen = accum 2 Ar Ar r Oxygen reacts at the surface, not in this region C O CO R0 2 2 2 4 r 4 r + = W W 0 0 O2 r+ r + r r r 2 2 W r W r Ar Ar + r r R r Divide by -4 r: = 0 r ( ) 2 d W r Ar dr ) Take limit as r 0: CO2 = 0 Put WAr in terms of conc of oxygen (CA) dC dr ( A = + + D y W W W De: effective diffusivity A e A A B dC dr d dr For every mole of O2 that enters, a mol of CO2 leaves WO2=-WCO2 dC d D dr dr A = D W A e dC dr Plug WAr into mole balance: 2 2 A A = r 0 = r 0 Divide out De: e Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-26 Mole Balance on O2 From r to r+ r (2) d dr dC dC dr dC dr = 1 2 r 2 2 A A = r K + r 0 C O CO R0 1 2 2 K K O2 r+ r 1 = = + dr C K A A 2 r Use boundary conditions to determine the concentration profile (CA/CA0) in terms of the various radii (R, R0 & r) At r = R0, CA= CA0 and at r = R, CA= 0 First use CA=0 when r = R to determine K2 K K r R R r 1 1 C K R R ( ) ( ) A0 1 0 C K 1R 1R A0 r R K R K R 1 1 = = + = C 0 K K A 2 2 CO2 1 1 Next solve for when r = R0 & CA=CA0 1 1 = C K = + C For any r: A 1 A K R K R Take the ratio to determine CA/CA0 1 1 = = + C A0 1 A0 0 C C 0 1R 1r 1R 1R K 1R 1r C A = 1 A = 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-27 Oxygen Concentration Profile & Flux C 1R 1r C 1R 1R Oxygen concentration Profile at time t CA: oxygen concentration CAb = CA0 A = + C O CO R0 2 2 A0 0 O2 r+ r 1 r 0.8 R 0.6 C C A 0.4 A0 CO2 Finally determine the flux of oxygen to the surface of the core: 0.2 0 0 10 r 20 R0 R (center) (core) dC dr A = D W A e ( ) ( ) 1R 1r C D C d dr C 1R 1r A0 1R 1R e A0 A0 1R 1R = = D W W = C A e A A ( ) 2 1R 1R r 0 0 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-28 Mass Balance on Carbon (C) + C O CO In out + gen = accumulation R0 2 2 4 3 O2 3 C C d R r+ r 2 + = 0 0 r'' 4 R c dt r Elemental C does not enter or leave the surface R Change in the mass of the carbon core r C: rate of C gen. per unit surface area of core (mol/s m2) C: density of solid C C: fraction of the volume of the core that is C = CO2 4 3 3 r'' dR dt C C d R c = Simplify mass balance: 2 C C r'' 4 R c dt The rate of carbon disappearance (-dR/dt) is equal to the rate of oxygen flux to the surface of the core, -WO2 = WCO2, and this occurs at a radius of R so: e A0 C A B 0 1R 1R D C R R R D C e A0 2 = = = r'' = r'' - W W C ( ) 2 r 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-29 Time Required to Shrink Core to Radius R R0 D C R R R r'' dR dt e A0 2 c -r'' = = O2 + C O CO c r+ r 2 2 C C 0 Substitute r c into -dR/dt, get like terms together, integrate, & solve for t ( R 0 D C t D C dR dt 1 r e A0 = 2 C C R R R 0 R ) R t D C Integrate over 0 to t & R0 to R 3 0 D C 3R 2 e A0 R R R = dR dt 0 C C 0 CO2 R 2 2 3 2 3 R R R R 3R R R 3R 0 2 e A0 e A0 + = t = 2 2 0 0 C C 0 C C R0 2 2 2 3 Get common denominators D C R R R R 3R 0 2 0 3 e A0 + = t C C 2 0 2 2 2 2 2 3 3 D C D C 3R R 6R R 3R R 6R 3R 2R 2R 6R 2R 6R 0 0 6 e A0 0 0 0 e A0 = = t t C C C C 6 0 0 0 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-30 Time Required to Shrink Core to Radius R + C O CO 2 2 R0 2 2 3 D C 3R R 6R R 2R 6R 0 0 6 e A0 Solve for t: = t O2 r+ r C C 0 0 2 2 3 C C Factor out R02/6 3R R 6R R 2R 6R 0 0 6 r = t D C 0 0 e A0 R 2 2 3 R 3R R 2R R C C 0 6D C Factor out -1 = 1 t 2 3 e A0 0 0 CO2 2 3 2 2 3 2 R 3R R 2R R R R R R R C C 0 6D C C C 0 6D C + = 1 3 + = 1 t 2 t 2 3 e A0 0 0 e A0 0 0 2 3 At the core of the catalyst particle, R=0, then: 2 2 R 0 0 R C C 0 6D C = 1 3 + C C 0 6D C t 2 = t R R 0 0 e A0 e A0 Complete regeneration Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-31 L20: Internal Diffusion Effects in Spherical Catalyst Particles Internal diffusion: diffusion of the reactants or products from the external pellet surface (pore mouth) to the interior of the pellet. (Chapter 12) When the reactants diffuse into the pores within the catalyst pellet, the concentration at the pore mouth will be higher than that inside the pore and the entire catalytic surface is not accessible to the same concentration. Though A is diffusing inwards, convention of shell balance is flux is in direction of increasing r. (flux is positive in direction of increasing r). In actuality, flux of A will have a negative sign since it moves inwards. CAs Porous catalyst particle CA(r) CAb Internal diffusion External diffusion External surface Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
Basic Molar Balance for Differential Element L19-32 CAs An irreversible rxn A B occurs on the surface of pore walls within a spherical pellet of radius R: R 2 W 4 r Rate of A in at r = WAr area = r Ar r r+ r 2 W 4 r Rate of A out at r - r = WAr area = The mole balance over the shell thickness r is: IN - OUT + GEN =ACCUM Ar r r Spherical shell of inner radius r & outer radius r+ r ( ) 2 2 2 A 4 r 4 r + 4 r = W W r r 0 Ar r Ar r r m c Volume of shell r A: rate of reaction per mass of catalyst (mol/g s) c: mass of catalyst per unit volume of catalyst (catalyst density) rm: mean radius between r and r - r ( Ar dr ) 2 d W r Divide by -4 r & take limit as r 0 Differential BMB in spherical catalyst particle 2 A = r r 0 c Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-33 Diffusion Equation (Step 2) IN - OUT + GEN =ACCUM CAs ( ) 2 2 2 A 4 r 4 r + 4 r = W W r r 0 Ar r Ar r r m c R Steady state assumption implies equimolar counter diffusion, WB = -WA (otherwise A or B would accumulate) A A e e cD D dr Must use effective diffusivity, De, instead of DAB to account for: 1) Tortuosity of paths 2) Void spaces 3) Pores having varying cross-sectional areas r r+ r dy dC dr A = = W bulk diffusivify D ~ A pellet porosity (Vvoid space/Vvoid & solid) (typical ~ 0.4) constriction factor (typical ~ 0.8) p c p = D D e AB tortuosity (distance molecule travels between 2 pts/actual distance between those 2 pts) (typical ~ 3.0) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-34 Diffusion & Rxn in a Spherical Catalyst 2 Ar BMB: W 4 r CAs ( Ar d r ( ) 2 2 A 4 r + 4 r = W r r 0 r Ar r r m c ) 2 d W r 2 A = r r 0 c dy dr dC dr A A = = R Diffusion: cD D W A e e r mol m Write the rate law based on surface area: n = r'' k" C A n A 2 s catalyst surface area mass of catalyst mol cat s = = S -r' r '' S Relate r A to r A by: a A A a g ) ( 2 d W r Insert the diffusion eq & the rate eq into the BMB: Ar dr 2 A = BMB: r r 0 c dC dr d dr + Boundary Conditions: CA finite at r=0 CA = CAs at r =R 2 2 n A = D r r S k" C 0 e C a n A Solve to get CA(r) and use the diffusion equation to get WAr(r) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-35 Dimensionless Variables + dr C (Psi) C ( e D 2 d 0 d Thiele modulus for rxn of nthorder n Subscript n = reaction order n is small: surface reaction is rate limiting n is large: internal diffusion is rate limiting C 1 C a 1st order rxn: small 1: surface rxn control, significant amount of reactant diffuses into pellet interior w/out reacting large 1: surface rxn is rapid, reactant is consumed very closed to the external surface of pellet (A waste of precious metal inside of pellet) dC d dr r R 2 2 n A Put into dimensionless form = D r r S k" C 0 e C A n A n 2 n 1 s k" S R C 0 k" S R C A 2 2 n a c C As n a c A = = = = n n ) R D As A s e 2 Boundary Conditions: =1 at =1 d d 2 n + = n =finite at =0 2 "a" surface rxn rate "a" diffusion rate 2 = n small 1 C C A sinh sinh The solution for A 1 = = medium 1 As As 1 large 1 R r=0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-36 Internal Effectiveness Factor, Internal effectiveness factor: (1) the relative importance of diffusion and reaction limitations (2) a measurement of how far the reactant diffuses into the pellet before reacting ( ) actual observed overallrate of rxn rate of reactionif entire interior surface were exposed to C = & T As s ( ) r' r' mass of catalyst mass of catalyst r r'' r'' A A A = = = ( ) As r As As For example, when n=1 (1st order kinetics, -r As ) ( ) d C d d 2 2 A r 4 R D C 4 R D ( ) 2 e As e 4 R W d Asr R = 3 = 1 = 3 r R = = = 4 3 4 3 4 3 3 ( ) R ) ) S k" C As r R S k " C R c a 1 As c a 1 A s ( ( x x + e e 2 x x 3 + cosh x e e e e ( ) = coth 1 = where coth x=sinh x 1 1 2 x x x x e e 2 1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-37 Internal Diffusion & Overall Rxn Rate quantifies how internal diffusion affects the overall rxn rate ( ) A As r'' r'' = Effectiveness factor vs n 1 0.8 0.6 Reaction limited 0.4 0.2 Internal diffusion limited 0.1 0.2 1 2 4 6 8 10 1 As particle diameter , n , 1, rxn is surface rxn limited As particle diameter , n , 0, rxn is diffusion limited This analysis was for spherical particles. A similar approach can be used to evaluate other geometries, non-isothermal rxn, & more complex rxn kinetics Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-38 Effectiveness Factor & Rxn Rate c 1 a k S D 3 ( ) ( ) ( ) = R = = r As r 1 As k C S = coth 1 1 A a 1 1 2 1 e R 1 surface-reaction-limited 1 D 3 3 R k e = when ,( 30) can be simplified to: , 1 1 S 1 1 c a 1 is large, diffusion-limited reaction inside the pellet (external diffusion will have a negligible effect on the overall rxn rate because internal diffusion limits the rxn rate) D 3 R k r 3 e S ( ) A = = coth 1 internal-diffusion-limited: 1 1 2 1 As r 1 c a e a 1 D S k 3 R D 3 R k = -r C ( ) e = r 1 As C k S A As ( ) = r 1 As k C S A a A a S c 1 c a Overall rate for 1st-order rxn Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-39 Clicker Question ( ) = r 1 As k C S D 3 R k D 3 R k ( ) A a e = e S r 1 As C k S A a S Overall rate for 1st-order rxn 1 c a 1 c a When the overall rate of rxn when the reaction is limited by internal diffusion, which of the following would decrease the internal diffusion limitation? (a) decreasing the radius R of the particle (b) increasing the concentration of the reactant (c) increasing the temperature (d) increasing the internal surface area (e) Both a and b Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L19-40 Total Rate of Consumption of A in Pellet, MA (mol/s) At steady state, net flow of A into pellet at the external surface completely reacts within the pellet Overall molar rxn rate = total molar flow of A into catalyst pellet MA = (external surface area of pellet) x (molar flux of A into pellet at external surface) MA =the net rate of reaction on and within the catalyst pellet C C A d C dC dr dC dr As r As R A = 2 A 2 = 4 R M D = 4 R W M A e A Ar = r R d = r R R = r R C C A d d d D C R 2 As r R = 4 R e As M D C = M 4 R A e As A = 1 d = r R Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.