Understanding Full Adder and Full Subtractor Circuits
Full Adder and Full Subtractor are essential combinational circuits used in digital electronics for addition and subtraction operations. A Full Adder calculates the sum of three bits, while a Full Subtractor performs subtraction considering borrow operations. They consist of input and output variables with defined truth tables and Boolean functions for simplification. Learn about their functioning, truth tables, simplification equations, and how they operate with detailed examples and diagrams.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
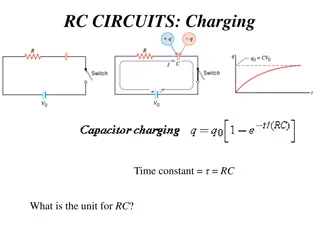
Full adder A full adder is a combinational circuit that forms the arithmetic sum of three bits. It consists of three inputs and two outputs. Two of the input variables, denoted by x and y , represent the two significant bits to be added. The third input, z , represents the carry from the previous lower significant position. The two outputs are designated by the symbols S for sum and C for carry. The binary variable S gives the value of the least significant bit of the sum. The binary variable C gives the output carry formed by adding the input carry and the bits of the words.
Truth table X, Y, Z represents the inputs C, S represents the outputs S = x y z + x yz + xy z + xyz C = x yz + xy z + xyz + xyz 1 1 1 0 1 0 1 1 + 10 0 0
Simplification of Sum equation S = x y z + x yz + xy z + xyz S = x y z + xyz + x yz + xy z S = z(x y + xy) + z (x y + xy ) S = z(x y + xy ) + z (x y + xy ) S = z(x y) + z (x y) S = x y z As (x y + xy) = (x y + xy ) As (x y + xy )= (x y)
Simplification of Carry equation using two approaches (k-map and Axioms) C = x yz + xy z + xyz + xyz Put the values in K map Alternate solution C = x yz + xy z + xyz + xyz C = z(x y + xy ) + xy(z + z) C = z(x y) + xy C=xy+xz+yz
X Y Z
Full subtractor A full subtractor is a combinational circuit that performs a subtraction between two bits, taking into account that a 1 may have been borrowed by a lower significant bit. Input variables are minuend (X), subtrahend (Y), and previous borrow (Z); output variables are difference (D) and output borrow (B). It performs the operation X Y Z. It should be noted that the weight of the output borrow bit is -2, while the weight of the output difference bit is +1.
full subtractor Works as : x-y-z 1 1 ----------------------------------- 0 0 0 1 0 10 0 1 1
Full subtractor The truth table of the full subtractor is shown. The simplified Boolean functions for the two outputs are: D = X Y Z + X YZ + XY Z + XYZ Can be simplified to D = X Y Z B = X Y Z+X YZ + X YZ +XYZ Can be simplified to B = X Y+X Z+YZ X Y Z B D 0 0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 1 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 1 1
Full subtractor D = X Y Z B = X Y Z+X YZ + X YZ +XYZ Can be simplified to B = X Y Z+XYZ+X YZ + X YZ B = Z(X Y +XY) + X Y(Z +Z) B = Z (X Y+ XY ) + X Y(1) B = z(X Y) +X Y
Binary Adder Binary Adder A binary adder is a digital circuit that produces the arithmetic sum of two binary numbers. It can be constructed with full adders connected in cascade, with the output carry from each full adder connected to the input carry of the next full adder in the chain. Addition of n-bit numbers requires a chain of n full adders or a chain of one-half adder and n - 1 full adders
Binary adder Example: 1 1 1 0 1 1 1 0 0 1+ ----------- 10 1 0 0
BCD Adder BCD Adder
BCD Adder BCD Adder When the sum of two digits is less than or equal to 9 then the ordinary 4-bit adder can be used But if the sum of two digits is greater than 9 then a correction must be added I.e adding 0110 We need to design a circuit that is capable of doing the correct addition
BCD Adder BCD Adder The cases where the sum of two 4-bit numbers is greater than 9 are in the following table: S4 S3 1 S2 0 S1 1 S0 0 0 10 0 1 0 1 1 11 0 1 1 0 0 12 0 1 1 0 1 13 0 1 1 1 0 14 0 1 1 1 1 15 1 0 0 0 0 16 1 0 0 0 1 17 1 0 0 1 0 18
BCD Adder Whenever S4=1 (sums greater than 15) Whenever S3=1 and either S2 or S1 or both are 1 (sums 10 to 15) The previous table can be expressed as: X = S4 + S3 ( S2 + S1) So, whenever X = 1 we should add a correction of 0110 to the sum.
Inputs:[A]=0101, [B]= 0011, Co=0 0011 0101 0 1 0 0 0 0 0 0 1000 1 1 0 0 0 0000
Inputs:[A]=0111, [B]= 0110, Co=0 0110 0111 0 1 1 0 1 1 1 1 1101 1 0 0 1 1 0110
Cascading BCD Adders The previous circuit is used for adding two decimal digits only. That is, 7 + 6 = 13 . For adding numbers with several digits, a separate BCD adder for each digit position must be used. For example: 2 4 7 BCD Adder BCD Adder 5 3 8 + -------------------- ? BCD Adder
Example Determine the inputs and the outputs when the above circuit is used to add 538 to 247. Assume a CARRY IN = 0 Solution: Represent the decimal numbers in BCD 247 = 0010 0100 0111 538 = 0101 0011 1000 Put these numbers in registers [A] and [B] [A] = 0010 0100 0111 [B] = 0101 0011 1000
Example 0 0 1 0 0 1 0 0 0 1 1 1 0 0 1 0 0111 1000 0101 0 1 0 1 0 0 1 1 1 0 0 0