Understanding Fractions: A Brief Historical Overview
Fractions have been integral to mathematics since ancient times, with civilizations like the Greeks utilizing them in various mathematical pursuits. This article explores the concept of fractions, their representation, and usage, along with historical insights into their development by ancient mathematicians such as the Greeks and Indians. The evolution of fractions from whole numbers to rational numbers is traced, highlighting their significance in mathematical calculations and arithmetic operations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Mavzu:Son tushunchasini kengaytirish masalasi. Kasr va manfiy son tushunchasini vujudga kelishi haiqdagi qisqacha tarixiy ma lumotlar. Reja: 1.Kasr tushunchasining hosil bo lishi haqida qisqacha tarixiy ma lumot 2.Kasr sonlarningyozilishi va o qilishi 3.Sonlar haqida umumiy ma lumot.
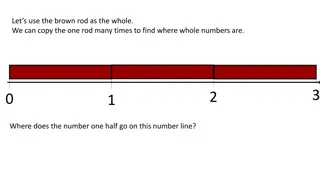
Kasr (arabcha: - bolak, parcha) matematikada birning bitta yoki bir nechta qismidan (bo lagidan) iborat son. Kasr ikkita butun sonning nisbati bilan ifodalanadi:m/n. Bu yerda m kasrning maxraji, n bo lsa surati deyiladi. Maxraj chiziqning ostiga (yoki ketiga), surat bo lsa, chiziqning ustiga (yoki oldiga) yoziladi. Maxraj bir sonni necha bo lakka bo linganini ko rsatadi, surat bo lsa shu kasrda shunday ulushlardan nechta borligini ko rsatadi. Masalan, va 3/4 u kasr teng uch bo lakni ifodalashini ko rsatadi. Maxraj bo lsa 4 dir va u to rtta bo lak bir bo lib butunni hosil qilishini anglatadi. Matematikada a/b ko rinishida yozsa bo ladigan barcha sonlar ratsional sonlar to plamiga kiradi. Bu yerda a va b butun sonlardir va b 0 ga teng emas (b 0). Kasr sonlar yaqqol surat yoki maxrajli bo lmasligi ham mumkin, masalan o nli kasr, foiz, manfiy darajalar (mos ravishda 0,01, 1% va 10 2; bularning har biri 1/100 ga teng). Butun sonni ham maxraji 1 ga teng kasr ko rinishida yozish mumkin: masalan 7 va 7/1 bir-biriga teng.
Yunonlar surati bir bolgan kasrlardan foydalanishgan. Eramizdan avvalgi taxminan 530-yilda yunon faylasufi Pifagorning shogirdlari ikkining kvadrat ildizini kasr ko rinishida yozib bo lmasligini aniqlashgan. Eramizdan avvalgi taxminan 150- yilda hindistonlik jainchi matematiklar Sthananga sutra (talaffuzi: Sananga sutra) asarini yozishgan. Bu asarda sonlar teoriyasi, arifmetik amallar va kasrlar ustida amallar haqida yozilgan. Bir sonni ikkinchisi ostida yozish va kasrlarni hisoblash usullari bizning eraning 499-yili atrofida Aryabhatta yozgan asarda uchraydi. . Sanskrit adabiyotlarda kasrlar yoki ratsional sonlar doim butun son va uning ketidan kasr son ko rinishida yozilgan. Kasr son butun son yozilgan qatorning ostiga yozilgan. Kasrning o zi ikki qatorda yozilgan. Birinchi qatorda yozilgan surat amsa deb atalgan, ikkinchi qatorga yozilgan maxraj cheda deb atalgan. O nli kasrlarning kelib chiqishi haqida Dirk Jan Struik bunday deb yozadi. "O nli kasrlarni hisobda ishlatishni keng foydalanishga kirgizgan asar deb 1585-yil Leydenda chop etilgan De Thiende flamand pamfletini aytish mumkin. O sha paytda Niderlandiyada yashagan matematik Simon Stevin (1548-1620) asarni fransuz tiliga o girgan. Xitoy matematiklari o nli kasrlardan Stevindan bir necha asr avval foydalanishgani rost. Fors astronomi Al-Kashi Arifmetika kaliti asarida oltmishli sanoq sistemasidan va o nli kasrlardan foydalangani ham rost. (15-asr boshlari, Samarqand) Fors matematigi Jamshid al-Kashi o nli kasrlarni 15-asrda o ylab topganman deb aytsa ham, J. Lennart Berggrenga ko ra u adashgan. Chunki o nli kasrlar undan 5 asr oldin, ya ni 10-asrda yashagan Bog dodlik matematik Abu'l-Hasan al-Uqlidisi ishlarida uchraydi.
Manfiy sonlar noldan kichik haqiqiy sonlar; musbat sonlarning qarama-qarshisi (qarang Qarama- qarshi son). Masalan, -2, -1 va h.k. Manfiy sonlar tushunchasi VI-XI asrlarda Hindistonda yaratilgan. Manfiy sonlarlar sonlar o qida sanoq boshidan, ya ni nol nuqtadan chap tomonda tasvirlanadi. Haqiqiy sonlar - har qanday musbat, manfiy son yoki nol. Haqiqiy sonlar to plami ratsional sonlar va irratsional sonlar to plamining birlashmasidan iborat. Haqiqiy sonlar to plami son o qi deb ham ataladi va R bilan belgilanadi. chiziqli tartiblangan to plam va, ko paytirish, qo shish amallariga nisbatan maydon tashkil qiladi. Haqiqiy sonlar to plami bilan to g ri chiziq nuqtalari o rtasida, tartiblanganlikni saqlagan holda, o zaro bir qiymatli moslik o rnatish mumkin. Haqiqiy sonlar to plamining muhim xususiyatlaridan biri uning uzluksizligidir. Uzluksizlik prinsipi turli shakllarda bayon qilinishi mumkin. Haqiqiy sonlar nazariyasi matematikaning muhim masalalaridan biri bo lib, bu nazariya 19-asrning 2-yarmida Veyershtrass, R.Dedekind, G.Kantor tomonidan yaratilgan. Barcha fizik kattaliklarni o lchash natijalari Haqiqiy sonlar bilan ifodalanadi. Aksioma - aksios so zidan kelib chiqan bo lib shubha qilinmaydigan tasdiqni bildiradi. Natural sonlar haqidagi aksiomalar grek O. Piano nomi bilan bog liq. U birinchi marta quyidagi aksiomalar sistemasining yaratdi. Natural sonlar qatorida shunday bir element mavjudki u hech bir sondan keyin kelmaydi. U 1 sonidir. Ixtiyoriy natural sondan keyin keladigan va undan bitta ortiq bo lgan bittagina son mavjud. Birdan boshqa har bir natural sondan oldin keladigan va undan bitta kam bo lgan bittagina natural son mavjud. Agar a va b natural sonlar teng bo lsa ulardan keyin keluvchi c va d lar ham teng bo ladi.
Shu tarzda, Q - bu raqamlarning ko'pligi, juda zarur bo'lgan narsalarni o'z ichiga oladi, chunki "dumaloq" raqamlar barcha mumkin bo'lgan operatsiyalarni tavsiflash uchun etarli emas. -Ratsional sonlar qo'shilishi, chiqarilishi, ko'paytirilishi va bo'linishi mumkin, amalningnatijasi ratsional son: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) (1/5) = 5/2. -Ratsional sonlarning har bir jufti orasida har doim boshqa ratsional sonni topish mumkin. Aslida, ikkita ratsional sonlar orasida cheksiz ratsional sonlar mavjud. Masalan, 1/4 va 1/2 mantiqiy asoslar orasida 3/10, 7/20, 2/5 (va yana ko'p narsalar) mantiqiy asoslari mavjud bo'lib, ularni o'nlik sifatida ifodalash orqali tekshirish mumkin. -Har qanday ratsional sonni quyidagicha ifodalash mumkin: i) butun son yoki ii) cheklangan (qat'iy) yoki davriy o'nlik: 4/2 = 2; 1/4 = 0,25; 1/6 = 0.16666666 - Xuddi shu sonni cheksiz ekvivalent kasrlar bilan ifodalash mumkin va ularning barchasi Q ga tegishli. Keling, ushbu guruhni ko'rib chiqaylik: Ularning barchasi o'nlik kasrni ifodalaydi0.428571 ... -Bir xil sonni ifodalovchi barcha ekvivalent kasrlardan, eng sodda bo'lgan kamaytirilmaydigan kasr kanonik vakil shu raqamdan. Yuqoridagi misolning kanonik vakili -3/7. Ratsional sonning o'nli tasviri Numeratorni maxrajga ajratganda ratsional sonning o nli shakli topiladi. Masalan: 2/5 = 0.4 3/8 = 0.375 1/9 = 0.11111 6/11 = 0.545454
Foydalanilgan adabiyotlar royxati: 1.Hamedova va boshqalar -Matematika Toshkent Turon Iqbol 2007-yil Internet tarmoqlari: fayllar.org www.ziyo.com