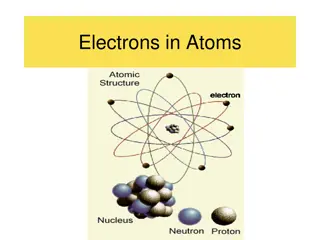
Understanding Bohr's Model of the Hydrogen Atom
Exploring the significance of Bohr's hydrogen model in physics, this lecture delves into the Bohr radius, the correspondence principle, and the success and limitations of his model. Discover how characteristic X-ray spectra contribute to our understanding of atomic structures, leading to the conclusion that the old planetary model is not sustainable due to the emission of electromagnetic radiation. Learn about the quantization of angular momentum and how Bohr formulated his model based on stationary states and transitions between them.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
PHYS 3313 Section 001 Lecture #13 Wednesday, Feb. 27, 2019 Dr. Jaehoon Yu Bohr Radius Bohr s Hydrogen Model The Correspondence Principle Importance of Bohr s Hydrogen Model Success and Failure of Bohr s Model Characteristic X-ray Spectra Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 1
Announcements Homework #3 End of chapter problems on CH4: 5, 14, 17, 21, 23 and 45 Due: Monday, March 18 Reminder: Midterm Exam In class next Wednesday, March. 6 Covers from CH1.1 through what we learn March 4 plus the math refresher in the appendices Mid-term exam constitutes 20% of the total Please do NOT miss the exam! You will get an F if you miss it. BYOF: You may bring a one 8.5x11.5 sheet (front and back) of handwritten formulae and values of constants for the exam No derivations, word definitions or setups or solutions of any problems! No Lorentz velocity addition formula! No Maxwell s equations! No additional formulae or values of constants will be provided! Special Colloquium this Friday 4pm, Friday, Mar. 1, SH101 Mr. Steve Battel, Battel Engineering, member of National Academy of Engineering Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 2
The Planetary Model is Doomed From the classical E&M theory, an accelerated electric charge radiates energy (electromagnetic radiation) which means total energy must decrease. Radius r must decrease!! Electron crashes into the nucleus!? Physics had reached a turning point in 1900 with Planck s hypothesis of the quantum behavior of radiation. Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 4
The Bohr Model of the Hydrogen Atom The assumptions Stationary states or orbits must exist in atoms, i.e., orbiting electrons do not radiate energy in these orbits. These orbits or stationary states are of a fixed definite energy E. (Niels Bohr was awarded Nobel in 1922 for this!) The emission or absorption of electromagnetic radiation can occur only in conjunction with a transition between two stationary states. The frequency, f, of this radiation is proportional to the difference in the energies of the two stationary states: E = E1 E2 = hf where h is Planck s Constant Bohr thought this has to do with the fundamental length of order ~10-10m Classical laws of physics govern the dynamic equilibrium of the stationary state but they do not apply to the transitions between stationary states. The mean kinetic energy of the electron-nucleus system is quantized as K = nhforb/2, where forb is the frequency of rotation. This is equivalent to the angular momentum of a stationary state to be an integral multiple of h 2p Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 5
How did Bohr Arrived at the angular momentum quantization? The mean kinetic energy of the electron-nucleus system is quantized as K = nhforb/2, where forb is the frequency of rotation in the given orbit. This is equivalent to the angular momentum of a stationary state to be an integral multiple of h/2 . Kinetic energy can be written 1 2mv2 K =nhf = 2 L = r p = mvr Angular momentum is defined as v=rw; 22pLf =nhf ,where =h w = 2p f The relationship between linear and angular quantifies K =1 1 2Lw =1 2p= n 2mvrw = L = nh Thus, we can rewrite 2 2pL = nh 2p Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 6
Bohrs Quantized Radius of Hydrogen The angular momentum is L = r p =mvr= n n mer ve= So the speed of an orbiting e can be written From the Newton s law for a circular motion 1 4pe0 2 e2 r2=meve e ve= Fe= 4pe0mer r So from the above two equations, we can get ve=n e r =4pe0n2 2 mer= 4pe0mer mee2 Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 7
Bohr Radius The radius of the hydrogen atom for the nth stationary state is rn=4pe0 mee2 2n2 =a0n2 Where the Bohr radius for a given stationary state is: ( 8.99 109N m2C2 ( ) 2 4pe0 mee2 2 1.055 10-34J s ) 9.11 10-31kg 2= 0.53 10-10m = a0= ( ) 1.6 10-19C ( ) The smallest diameter of the hydrogen atom is d = 2r1= 2a0 10-10m 1A OMG!! The fundamental length!! n = 1 gives its lowest energy state (called the ground state) Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 8
Ex. 4.6 Justification for non- relativistic treatment of orbital e Are we justified for the non-relativistic treatment of the orbital electrons? When do we apply relativistic treatment? When v/c>0.1 Orbital speed: Thus 1.6 10-16 ( 9.1 10-31 ( e ve= 4pe0mer ) 9 109 ) 0.5 10-10 ( ) ( )<0.01c ve= 2.2 106m s ( ) Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 9
Uncertainties Statistical Uncertainty: A naturally occurring uncertainty due to the number of measurements Usually estimated by taking the square root of the number of measurements or samples, N Systematic Uncertainty: Uncertainty due to unintended biases or unknown sources Biases made by personal measurement habits Some sources that could impact the measurements In any measurement, the uncertainties provide the significance to the measurement Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 10
The Hydrogen Atom Rydberg Equation Recalling the total E of an e in an atom, the nth stationary states, En e2 8pe0rn n2 1.6 10-19 ( ) 2 -E0 e2 e2 ( ) En= - = - 8pe0a0n2= =13.6 eV = E0= 8p 8.85 10-12 ( )0.53 10-10 ( ) 8pe0a0 where E1 is the lowest energy or ground state energy Emission of light occurs when the atom is in an excited state and decays to a lower energy state (nu n ). hf =Eu-El where f is the frequency of a photon. = R c=Eu- El 1 l=f 1 nl 2-1 1 nl 2-1 =E0 2 2 hc hc nu nu R = E0hc R is the Rydberg constant. PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu RH=1.096776 107m-1 Wed. Feb. 27, 2019 11
Transitions in the Hydrogen Atom Lyman series (n=1): The atom will remain in the excited state for a short time before emitting a photon and returning to a lower stationary state. All hydrogen atoms exist in n = 1 (invisible). Balmer series (n=2): When sunlight passes through the atmosphere, hydrogen atoms in water vapor absorb the wavelengths (visible). Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 12
Fine Structure Constant The electron s speed on an orbit in the Bohr model: n mern me mee2 n e2 1 n ve= = = 4pe0n2 2 4pe0 On the ground state, v1 = 2.2 106 m/s ~ less than 1% of the speed of light The ratio of v1 to c is the fine structure constant, . a c= ( 1.055 10-34J s ( e2 v1 4pe0c= ) 1.6 10-19C ) 3 108m s ma0c= ( ) 2 8.99 109N m2C2 1 ( ) 137 Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 13
Ex. 4.7: Determine the longest and shortest wavelengths observed in Paschen Series (n=3) We use the equation 1 l= R nl nu 1 lMax 42 1 2-1 2 ( ) = 1 32-1 5.335 105m-1 =1.0974 107 ( ) ) lMax=1875 nm ( =1.219 106m-1 lMin=820 nm 1 1 32-1 =1.0974 107 lMin 2 ( ) Wed. Feb. 27, 2019 PHYS 3313-001, Spring 2019 Dr. Jaehoon Yu 14