Trigonometric Graphing and Shifts Explained
Explore the concepts of determining period, amplitude, vertical and horizontal shifts in trigonometric functions. Learn how to identify and graph functions with various shifts.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Warm Up: Determine the period and amplitude of the function. Then, graph it! y = -9cos(2x)
MORE TRIGONOMETRIC GRAPHING
Lets shift! https://www.youtube.com/watch?v=BQ4QzTc G90g https://www.youtube.com/watch?v=zjSgkoaL _5A
Recall from yesterday: y = asin(bx) y = acos(bx) Amplitude of the graph = a Period of the graph = b 2
Vertical Shift (k) y = asin(b(x - c)) + d y = acos(b(x c)) + d When a graph moves up or down, it is called a vertical shift. d tells us which direction and how far to shift.
Example 1: State the direction and distance that each function has shifted. 1. y = cos(x) 3 2. y = sin(x) 2 3. y = sin(x) + 4 4. y = cos(x) +
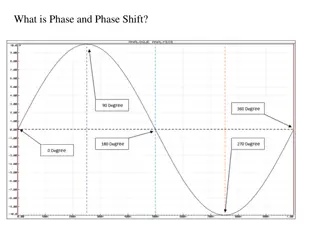
Phase Shift (h) y = asin(b(x - h)) y = acos(b(x - h)) When a graph shifts left or right, it is called a phase shift. h tells us the direction and how far to shift. Note that h is subtracted, so go the opposite direction that you would assume.
Example 2: State the direction and distance that each function has shifted. 1. y = sin(2(x + )) 2. y = cos(x ) 3 3. y = cos(x + ) 4 3 4. y = sin(x ) 2
Putting it all together! y = asin(b(x c)) + d y = acos(b(x c)) + d Amplitude of the graph = a Period of the graph = 2 b Horizontal translation = c (note: opposite direction) Vertical translation = d