Trees in Data Structures and Algorithms

In this chapter, you will learn about trees as a data structure, including definitions, types, and key concepts such as nodes, edges, levels, and heights. Trees play a crucial role in organizing data efficiently, and understanding them is essential for mastering algorithms and data structures.

• Data Structures
• Algorithms
• Trees
• Nodes
• Hierarchies

sidra Follow

Uploaded on Jul 10, 2024 | 4 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Data structure and algorithm 2 Trees 1

2. Objectives After studying this chapter, the student should be able to Define trees , Learn the concepts and principles involved in Trees Binary trees 2

3. DATA STRUCRE Data structure ? A data structure is an arrangement of data in a computer's memory so as to be used effectively. There are two types of data structure . 1-Linear data structure. 2- Non linear structure . How can we decide which data structure to be used? -What needs to be stored -Cost of operation -Memory usage . -Ease of implementation . 3

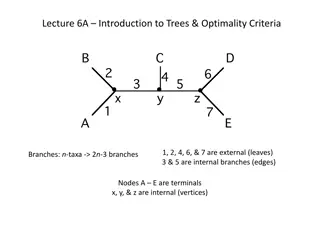
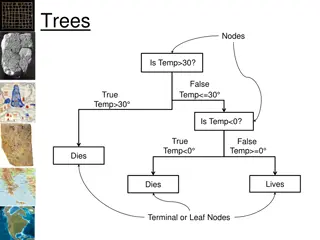
4. Trees Trees:- A tree is a (possibly non-linear) data structure made up of nodes or vertices and edges without having any cycle. The tree with no nodes is called the null or empty tree. A tree that is not empty consists of a root node and potentially many levels of additional nodes that form a hierarchy . . . 4

5. Trees definitions Root The topmost node in a tree. Parent The converse notion of a child. Siblings Nodes with the same parent. . Descendant a node reachable by repeated proceeding from parent to child Ancestor a node reachable by repeated proceeding from child to parent. .. - - 5

6. Trees definitions Leaf a node with no children . . - Internal node a node with at least one child . . - External node a node with no children . . . - Degree number of sub trees of a node . - 6

7. Trees definitions Edge connection between one node to another - Path a sequence of nodes and edges connecting a node with a Descendant . Level The level of a node is defined by 1 + (the number of connections between the node and the root) ( + ) . - . 1 7

8. Trees definitions Height of tree The height of a tree is the number of edges on the longest downward path between the root and a leaf THE - . . . Height of node The height of a node is the number of edges on the longest downward path between that node and a leaf Depth The depth of a node is the number of edges from the node to the tree's root node. - THE Forest A forest is a set of n 0 disjoint trees - 0 . THE - . 8

9. Binary tree Definition: A binary tree is a finite set of nodes which is either empty or consists of a root and two disjoint binary trees called the left sub tree and the right sub tree. , : 9