Transverse Wave Motion in Physics
Explore the concepts of transverse wave motion, velocities in wave motion, group velocity, dispersion, and the transverse wave equation on a string. Visual examples and explanations enhance the understanding of these fundamental principles in physics.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Transverse Wave Motion 17THSEPTEMBER 2019 1
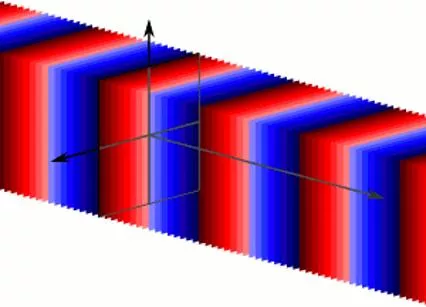
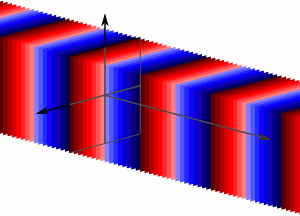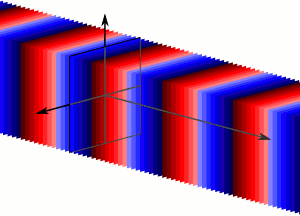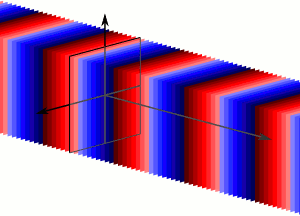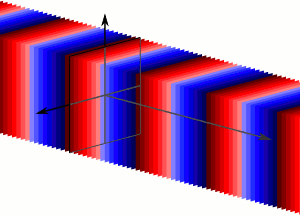
Concept of Plane wave A typical representation of a wave propagating in space The propagating wave causing the individual oscillators in the medium to oscillate Overall oscillation of the oscillators with the same phase in the same plane forms the travelling plane wave. Note : each color represents a different phase of the wave. https://en.wikipedia.org/wiki/Plane_wave 2
Velocities in wave motion For a mechanical wave, the individual oscillators which make up the medium do not progress through the medium with the waves. The three velocities in wave motion are 1. The particle velocity 2. The wave or phase velocity 3. The group velocity For a monochromatic wave, the group velocity and the wave velocity are identical. 3
Example of the group velocity Propagation of a light pulse in a dispersive medium. Note that the phase fronts of different frequency components propagate with different velocities, and the pulse propagates with the group velocity, which is lower than all the phase velocities; No temporal broadening due to the propagation taking place in a nondispersive medium. https://www.rp-photonics.com/group_velocity.html 4
White light pulse consists of an infinite fine spectrum of frequencies and moving with a group velocity. The wave velocity of each wavelength in the group is different. The phenomenon is known as dispersion. (GVD = Group Velocity Dispersion) http://slideplayer.com/slide/10965793/ 5
Example of dispersion http://www.koppglass.com/blog/optical-properties-of-glass-how-light-and-glass-interact/ 6
The transverse wave equation on a string A very short section of a uniform string has a vertical displacement. The wave equation relates the vertical displacement y to time t and position x. Given that the linear density and a constant tension T along a slightly extensible string, the wave equation is given as 2 2 2 1 c y x y t y t = = 2 2 2 2 T 7
Ideal string constraints In order for the wave equation to apply to the waves in a string, it must meet certain constraints. For an ideal string, it is assumed that 1. The string is perfectly uniform with a constant mass per unit length, and is perfectly elastic with no resistance to bending. 2. The string tension is presumed to be large enough so that gravity can be neglected. 3. Small segments of the string are presumed to move transversely in a plane perpendicular to the string, and that the displacements and slopes of segments of the string are small. http://hyperphysics.phy-astr.gsu.edu/hbase/Waves/waveq.html#c2 8
How to obtain the wave equation By applying the Newton s second law of motion, the horizontal force components on the element are cancelled. And, the vertical force components results in 2 y x y x y t = T dx 2 x dx + x According to the definition of the partial derivative, we have 2 2 2 1 c y x y t y t = = ; c is the wave velocity. 2 2 2 2 T 9
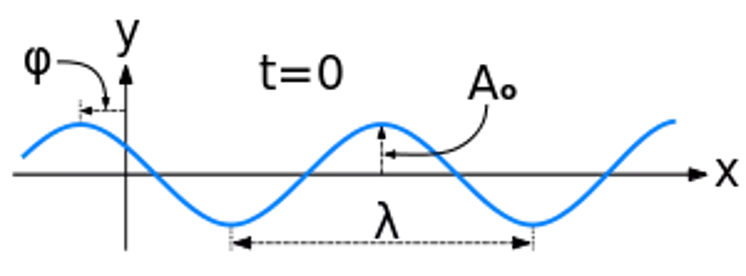
Solution of the wave equation : travelling wave The solution of the wave equation is a function of the variables x and t. The right and left travelling (or progressive) waves can be written as ( ) ( ) ( ) ( ) , sin ; moving to the left: -x direction y x t a t kx = + = , sin ; moving to the right: +x direction y x t a t kx Note : Initially, a wave function is given as y = asin( t0 kx0). At a later time t (>t0), the wave function becomes y = asin( t - kx). t0 kx0 = t kx and this leads to x > x0 . This suggests the right moving waveform. http://hyperphysics.phy-astr.gsu.edu/hbase/Waves/wavsol.html#c3 10
Characteristic impedance Any medium through which waves propagate will present an impedance to those waves. The impedance to progressive transverse waves is defined as the transverse impedance, transverse force transverse velocity F v = = Z The velocity v here is the particle velocity NOT the wave velocity. For a harmonic force, the ratio of force to velocity tells you how hard it is to move the object this depends both on how much inertia (e.g. linear density) the object has and on how strong the restoring force (e.g. tension) is. The impedance, represented a medium characteristic, can be either real (for lossless case) or complex (for loss case). 11
Characteristic impedance of a string The displacement of the progressive waves may be given as At the left end of the string, x = 0, the wave is rewritten as y = The string as a forced oscillator with a vertical force F0exp(i t) driving at one end. ( ) t kx i = y Ae F c i ( ) i t 0 e T The velocity is found to be c T ( ) i t = = v y F e 0 y x i t = = sin tan ; small F e T T T 0 The string characteristic impedance T c The constant tension T in the string is balanced by the force at the end of the string. = = Z c WHY? 12
Reflection and transmission of wave on a string at a boundary Waves on a string impedance 1c1 reflected and transmitted at the boundary x = 0 where the string changes to impedance 2c2 2c2 1c1 Boundary conditions at x = 0 : 1. geometrical condition : displacement is the same immediately to the left and right at x = 0 for all time (a continuity of the string) 2. dynamical condition : a continuity of the transverse force T( y /x) at x = 0, and therefore a continuous slope. 13
Incident, reflected and transmitted waves ( ( ( ) ) + ( ) , exp A t k x = Incident wave : , y x t 1 1 i ( ) , exp B t k x = Reflected wave : y x t 1 1 r ) ( ) exp A t k x = Transmittedwave: y x t 2 2 t 14
Determination of the reflection and transmission amplitude coefficients According to the boundary conditions (at x =0 for all t) + = BC 1 : y y y i r t + ( ) ( ) ( ) t k x t k x + t k x i i i = Ae B e A e 1 1 2 1 1 2 ( ) + = BC 2 : T y y T y i r t x x T c T c T c + = - - A B A 1 1 2 1 1 2 15
Reflection and transmission coefficients + B A Z Z Z Z 1 1 2 = Reflection coefficient of amplitude, 1 1 2 Z + 2 A A 2 1 Z = transmission coefficient of amplitude, Z 1 1 2 Note : these coefficients are independent of and hold for waves of all frequencies. What does it mean if Z2 = ? What does it mean if Z2 = 0? 16
Reflections of string at fixed end (Z = ) and at free end (Z = 0) At a fixed (hard) boundary, the displacement remains zero and the reflected wave changes its polarity (undergoes a 180ophase change) At a free (soft) boundary, the restoring force is zero and the reflected wave has the same polarity (no phase change) as the incident wave https://www.acs.psu.edu/drussell/demos/reflect/reflect.html 17
https://www.acs.psu.edu/drussell/Demos/reflect/reflect.html An incident wave travelling from a low density (high wave speed) region towards a high density (low wave speed) region. How do the polarities of the reflected and transmitted waves compare to the polarity of the incident wave? An incident wave travelling from a high density (low wave speed) region towards a low density (high wave speed) region. How do the polarities of the reflected and transmitted waves compare to the polarity of the incident wave? Anything wrong with this animation! 18
Example 1 A triangular shaped pulse of length l is reflected at the fixed end of the string on which it travels (Z2 = ). Sketch the shape of the pulse after a length (a) l/4 (b) l/2 (c) 3l/4 and (d) l of the pulse has been reflected. 19
Solution 20
Reflection and transmission of energy Now, let s consider what happens to the energy flow in a wave when it meets a boundary between two media of different impedance values. Generally, the energy flow or the rate at which energy is being carried along a unit length, mass , of the string as a simple harmonic oscillator of maximum amplitude A with travelling wave velocity of c is ( ) energy velocity 1 2 2 2 = A c This can be shown that the energy arriving at the boundary x = 0 is equal to the energy leaving the boundary. In other words, the energy is conserved. 21
Energy flow or rate of energy Due to the total energy of a unit length : E E E = + 1 2 1 2 2 2 = + my sy K U ( ) = = sin y A t kx ( ) cos y A t kx 1 2 1 2 2 2 2 2 = = = ; Energy per unit lenght E mA A s m 1 2 1 2 2 2 E x = ; For a lenght of the total energy becomes x A x 1 ( ) ( ) 2 2 2 2 = = ; rate of energy flow or power = 2 A x t A c c x t 22
The conservation of energy All energy arriving at the boundary in the incident wave leaves the boundary in the reflected and transmitted waves. energy arriving = energy leaving 1 1 2 2 1 1 2 2 1 1 2 2 1 2 2 2 1 2 2 1 2 2 2 = + 1 1 c A 1 1 c B 2 2 c A 1 2 2 2 1 2 2 1 2 2 2 = + Z A Z B Z A 1 1 2 2 2 1 2 2 1 = Z A Z A 1 1 Note : The proof requires the transformation of B1 and A2 to be in terms of A1. 23
The reflected and transmitted intensity coefficients 2 2 2 + Reflected Energy= Incident Energy 1 1 Z B Z A B A Z Z Z Z 1 1 2 = = 2 1 1 2 1 1 Z A Z A 2 4 Transmitted Energy= Incident Energy 1 2 Z Z Z + 2 2 = ( ) 2 2 Z 1 1 1 2 Note : if Z1 = Z2 no energy is reflected and the impedances are said to be matched. 24
Example 2 A transverse harmonic force of peak value 0.3 N and frequency 5 Hz initiates waves of amplitude 0.1 m at one end of a very long string of linear density 0.01 kg/m. Determine the rate of energy transfer along the string and the wave velocity. (ans : 3 /20 W and 30/ m/s) 25
1 2 2 rate of energy transfer = 2 c A solution F v = impedance Z = c ( ) = = sin Suppose y A t kx ( ) = cos v y A t kx . 0 3 . 0 3 5 0 1 N m F = = = = s z c ( ) . 2 A . 1 2 1 0 3 2 ( ) ( ) 2 2 2 2 = 0 1 5 . 0 1 . rate of energy transfer = 2 c A 3 20 0 3 = W . 1 . 30 = = = and m s c Z 0 01 26
The matching of impedances Impedance matching represents a very important practical problem in the transfer of energy. The concept of impedance matching is to have the impedance change slowly. An appropriate length and impedance of another string between two mismatched strings will eliminate energy reflection and match the impedance. 27
The analysis of the matching impedances To comply with the condition of matching impedances, the following ratio has to be unity, 2 3 3 Z A Z A Transmitted Energy= Incident E = 1 2 ne gy r 1 1 To derive the impedance and the length of the inserted piece of the string, the boundary conditions are that y and T( y/ x) are continuous across the junctions x = 0 and x = l. This gives 2 2 3 2 1 4 3 3 Z A Z A A A 13 r + Transmitted Energy Incident Energy 1 = = = ( ) ( ) 2 2 2 13 r 2 2 + + 1 cos sin 13 r k l 12 r 23 r k l 1 1 2 2 Two impedances to be matched when and the thickness of the coupling medium is 2 1 3 Z Z Z = 24 28
Standing waves on a string of a fixed length ( ) ( ) t kx t kx + i i = + y ae be The displacement on the string at any point is given by With the boundary condition that y = 0 at x = 0 and x = l at all times, thus ( 2 y = ( ) ) i t sin i ae kx The complete expression for the displacement of the nth harmonic is given by x ( )( i ) n c ) = + 2 cos sin sin y a t i t n n n x ( n c = + cos sin sin y A t B t This may be expressed as n n n n n ( )1 2 + = 2 A B a Where the amplitude of nth mode is given by n n 29
homework Problems : 4.12, 4.13, 5.9 30

 undefined
undefined


 undefined
undefined