Topic : Understanding Quadrilaterals
In day-to-day life, we encounter various objects shaped like quadrilaterals. This chapter explores different types of quadrilaterals, their properties, and the derivation of angle sum property for polygons. From defining plane curves to understanding the properties of trapezium and parallelogram, this topic covers a wide range of concepts related to quadrilaterals and polygons. Explore the characteristics of convex, concave, regular, and irregular polygons, and learn about the properties of rhombus, rectangle, and square. Discover the applications of curves in various fields like transportation and art, as well as their role in shaping roadways and railways.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Class : VIII Subject : Mathematics Topic : Understanding Quadrilaterals
UNDERSTANDING QUADRILATERALS PDF chapter link : https://drive.google.com/file/d/1xHRbuIebO0T14 7U4oFfInwsfJI-j96fS/view?usp=drivesdk WORK IS WORSHIP
LEARNING OBJECTIVES : The students will be able to : define a plane curve. identify the closed curves and open curves. define a polygon. name the different types of polygons. explain the different parts of a polygon. distinct between convex & concave polygons and also between regular and irregular polygons. understand the derivation of angle sum property of different polygons by forming triangles. apply the formula to find the sum of interior angles of a n-sided polygon. find the sum of exterior angles of a polygon. understand the properties of trapezium and parallelogram. learn the properties of rhombus, rectangle & square. WORK IS WORSHIP
INTRODUCTION In our day-to-day life, we often see around us many objects which are of the shape of a Quadrilateral. For example, the table top, the blackboard, each face of the duster, each page of a book, the floor, walls, ceiling and windows of a classroom. The word Quadrilateral is made up of two words quad which means four and the word lateral which means sides. In this Chapter, we shall study different types of Quadrilaterals and their properties. We know that a triangle is obtained by joining three non-collinear points in pairs. Similarly, if we have four points in a plane such that no three of them are collinear, then the figure obtained by joining them in an order is called a quadrilateral. WORK IS WORSHIP
PLANE CURVES : A plane curve is a curve that lies in a single plane or a plane surface like a paper. We can draw a plane curve by joining a number of points without lifting a pencil from the paper and without retracing any portion of the drawing other than single point. A plane curve may be closed or open. Closed Curves A curve that begins and ends at the same point is called a closed curve. WORK IS WORSHIP
Open Curves : A curve that does not end at its starting point is called an open curve. Simple Closed Curves : A closed curve which does not intersect itself is called a simple closed curve. WORK IS WORSHIP
Complex Closed Curves : Any closed curve which intersects itself is called a complex curve. Uses of curves : Curves are used in driving testing centres by transport department. Different curves are used by artists for making their arts. Curves are used in changing the alignment and direction of road and railways. It is also used in airports to connect runway and taxiway. Curves are also used in mountain or hilly areas where the road needs to climb heights. WORK IS WORSHIP
Polygons : Any closed geometrical plane figure made up of three or more line segments is called a Polygon. The above curves are polygons. WORK IS WORSHIP
Curves which are not polygons : WORK IS WORSHIP
Types of Polygons : Polygons can be classified according to the number of sides or vertices. A polygon having three sides is called a Triangle. A polygon having four sides is called a Quadrilateral. A polygon having five sides is called a Pentagon. A polygon having six sides is called a Hexagon. A polygon having seven sides is called a Heptagon. A polygon having eight sides is called a Octagon. A polygon having nine sides is called a Nonagon. A polygon having ten sides is called a Decagon. NOTE :Polygon comes from a Greek word, Poly means many and gon means angle . WORK IS WORSHIP
Names of Polygons : Name Sides Shape 3 Triangle (or Trigon) 4 Quadrilateral (or Tetragon) 5 Pentagon 6 Hexagon 7 Heptagon (or Septagon) 8 Octagon 9 Nonagon (or Enneagon) WORK IS WORSHIP
Sides Shape Name 10 Decagon 11 Hendecagon (or Undecagon) 12 Dodecagon 13 Triskaidecagon For polygons with 13 or more sides, it is easier to write 13 - gon , 14 - gon , ........ 100 gon etc. WORK IS WORSHIP
Convex & Concave Polygons : If the vertices of a polygon lie on the same side of the line containing any segment (sides of the polygon), then the polygon is called Convex Polygon. In the adjoining figure, with respect to line containing the line segment AB, the remaining vertices C,D,E & F lie on the same side. Similarly, with respect to line m containing the line segment CD, the remaining vertices A, B, E & F lie on the same side. In a convex polygon none of the diagonals goes outside the polygon as it travels from one vertex to the opposite vertices. In a convex polygon, each interior angle is always less than 180 . WORK IS WORSHIP
Convex Polygons WORK IS WORSHIP
If the vertices of a polygon lie on the both sides of the line containing any segment (sides of the polygon), then the polygon is called Concave Polygon In the adjoining figure, with respect to line m containing the line segment CD, the remaining vertices A,B & E, F lie on the opposite sides of the line. Similarly, with respect to line n containing the line segment DE, the remaining vertices A, F & B, C lie on the opposite sides of the line. In a concave polygon, some of the diagonals lie outside the polygon as they travel from one vertex to the opposite vertex. In a concave polygon, there is atleast one reflex interior angle - that is, an angle with a measure between 180 & 360 . n WORK IS WORSHIP
Concave Polygons WORK IS WORSHIP
Regular Polygon : A polygon having all the sides and all the interior angles equal is called a Regular Polygon. A Regular Polygon is both equilateral and equiangular. An equilateral triangle is a Regular Polygon because all the sides are of equal length and each interior angle is 60 . A square is a Regular Polygon because all its sides are of equal length and each interior angle measures 90 . Similarly, a polygon with five equal sides, six equal sides, seven equal sides, eight equal sides, etc and with equal angles are called as Regular Pentagon, Regular Hexagon, Regular Octagon respectively and so on. Equilateral Triangle Square Regular Pentagon Regular Hexagon WORK IS WORSHIP
Irregular Polygon : A polygon in which neither the sides nor the angles are equal is called an irregular Polygon. The triangles other than the equilateral triangle (Scalene Triangle, Isosceles Triangle, Right Angled Triangle) are Irregular Polygons. Quadrilaterals like rectangle, parallelogram, rhombus and trapezium are irregular Polygons because neither the sides nor the angles are equal. WORK IS WORSHIP
Parts of a Polygon : Adjacent Sides : Any two sides with a common vertex are called adjacent sides of a Polygon. In the figure, the sides (AB, BC) , (BC, CD), (CD, DE), (DE, EF) & (EF, FA) are the adjacent sides of the given hexagon. Adjacent Vertices : The point of intersection of two adjacent sides of a polygon is called its Vertex. Thus, the end points of the same side of a polygon are called adjacent vertices. In the figure (A,B), (B, C), (C, D), (D, E), (E, F) & (F, A) are adjacent vertices. Diagonal : Take any two vertices of a polygon which are not adjacent and join them. The line segment thus obtained is called the diagonal of the polygon. The line segment joining two vertices of a polygon which are not adjacent is called the diagonal of a polygon. In the figure, AC, AD, AE, BD, BE, BF, CE, CF & DF are the diagonals of the given polygon. WORK IS WORSHIP
Interior & Exterior of a Curve : The part of the plane which consists of the points, like A, B, C, D, E, F is called the interior part of the curve. The interior of the curve along with its boundary is called the region of the curve . (i) The part of the plane which consists of the points like P, Q, R is called the exterior part of the curve. In the figure (i) the points A, B, C, D, E & F lie in the interior part of the curve. In the figure (ii) the points P, Q & R lie in the exterior part of the curve. (ii) WORK IS WORSHIP
TRY THESE : Worksheet 1 Choose the convex and concave polygons from the given figures. 1. 2. Separate the regular and irregular polygons from the adjoining figures. WORK IS WORSHIP
Angle sum Property of a Polygon : Activity 1 : (Angle Sum Property of a Triangle) The sum of the measures of the three angles of a triangle is 180 . Draw any triangle ABC. Through the vertex A, draw a line l parallel to BC. From the figure, (alternate interior angles) & (alternate interior angles) Now, (Angle on a straight line) Sum of the angles of a triangle is 180 . WORK IS WORSHIP
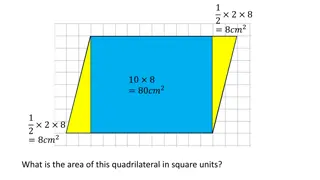
Activity 2 : (Angle sum property of a quadrilateral) The sum of the measures of four angles of a Quadrilateral is 360 or four right angles. Draw any quadrilateral ABCD. Divide it into two triangles by drawing a diagonal AC. You get six angles, i.e. . Use angle-sum property of a triangle to find the sum of angles of each triangle. In ........... (i) In , ......... (ii) Adding corresponding sides of (i) and (ii), we get Sum of angles of a quadrilateral is 360 or four right angles. WORK IS WORSHIP
Activity 3 (Angle sum property of a pentagon) The sum of the measure of the angles of a pentagon is 540 . Draw any pentagon ABCDE. From the vertex A, draw diagonals AD & AC. This divides the pentagon into three triangles. We know that the sum of The angles of a triangle is 180 . In ........ (i) In .......(ii) In ........(iii) By adding (i), (ii) & (iii), we get Arranging the angles :- Sum of the angles of a pentagon is 540 . WORK IS WORSHIP
Sum of interior angles of an n-sided polygon : From any one of the vertices, say A1 construct diagonals to the opposite vertices. There are altogether (n 2) triangles. Sum of angles of a triangle is 180 . Therefore, sum of interior angles of an n-sided polygon = For a regular polygon of n-sides, each interior angle = . Example 1 : Find the sum of interior angles a nonagon. Sol :- A nonagon has n-sides. Therefore, n = 9 Sum of all interior angles = = (9 2) x 180 = 1260 WORK IS WORSHIP
Example - 2 : Find the measure of each interior angles of a regular decagon. Solution : A decagon has 10 sides. Therefore n = 10. Each interior angle of regular decagon = = Example - 3 : Find the number of sides of a polygon if the sum of its interior angles is 1980 . Solution : Sum of interior angles of a polygon of n-sides = 1980 = 1980 the number of sides of the polygon is 13. WORK IS WORSHIP
The General Rule : sum of interior angles of a polygon = (n 2) x 180 Each interior angle of a regular polygon = (n 2) x 180 / n Polygon Sides Sum of interior angles Each interior angle Triangle 3 180 60 Quadrilateral 4 360 90 Pentagon 5 540 108 Hexagon 6 720 120 Heptagon 7 900 128.57... Octagon 8 1080 135 Nonagon 9 1260 140 ......... ........ ................ .............. Any polygon n (n 2) x 180 (n 2) x 180 / n WORK IS WORSHIP
Sum of the measures of the exterior angles of a polygon : Triangle In the adjoining figure, ABC, are the exterior angles. form a linear pair of angles. .......... (i) Similarly, .......... (ii) ........... (iii) By adding (i), (ii) & (iii) (sum of angles of a is 180 ) WORK IS WORSHIP
Quadrilateral In quadrilateral PQRS, are the exterior angles when the sides are produced in cyclic order. form a linear pair of angles. .............. (i) Similarly, .............(ii) .............(iii) ..............(iv) By adding (i), (ii), (iii) & (iv), WORK IS WORSHIP
Hexagon In the hexagon ABCDEF given in the adjoining figure, are the exterior angles when the sides are produced in cyclic order. Form a linear pair of angles. ...............(i) Similarly, ..................(ii) ...................(iii) ....................(iv) ....................(v) ....................(vi) By adding (i), (ii), (iii), (iv), (v) & (vi), Note :- Each exterior angle of a regular polygon of n-sides Sum of the measures of the exterior angles of any polygon is 360 . WORK IS WORSHIP
Example 4 : Find the measure of x in the given figure. Solution : We know that, sum of exterior angles of a polygon is 360 . Example 5 : Find the measure of the exterior angles in the given figure. Solution : We know that, sum of exterior angles of a polygon is 360 . The exterior angles are 119 , 119 + 1 = 120 & 119 + 2 = 121 . WORK IS WORSHIP
TRY THESE : Worksheet 2 1. A heptagon has four equal angles each of 132 and three other angles are equal to each other. Find the major of equal angles. The sum of interior angles of a polygon is 2700 . How many sides these polygon has ? Each interior angle of a regular polygon is double its exterior angle. Find the number of sides of the polygon. Find the number of sides of a regular polygon if each of its interior angle is 120 . Find the number of sides of a regular polygon whose each exterior angle has a measure of 45 . Find x in the following figures. (a) (b) x x 2. 3. 4. 5. 6. WORK IS WORSHIP
QUADRILATERALS : A polygon of four sides is called a quadrilateral. Or A closed plane figure bounded by four line segments is called a quadrilateral. In the adjoining diagram, ABCD is a quadrilateral. It has four sides : AB, BC, CD & DA four vertices : A, B, C & D four angles : Two diagonals : AC & BD ELEMENTS OF A QUADRILATERAL : A quadrilateral is formed by joining any four non-collinear points. Adjacent sides : Two sides having a common vertex are called adjacent sides. In the above figure, AB & BC, BC & CD, CD & DA, DA & AB are adjacent sides. WORK IS WORSHIP
Opposite sides : Two sides of a quadrilateral without any common vertex are called opposite sides. In the figure, AB & CD ; BC & AD are opposite sides. Adjacent angles : A pair of angles having a common arm are called adjacent angles. In the figure, are adjacent angles. Opposite angles : Two non-adjacent angles without any common arm are called opposite angles. In the figure, are opposite angles. Diagonals : The line segment joining a pair of opposite vertices are called diagonals. In the figure, AC & BD are the diagonals. Angle sum property of a quadrilateral : The sum of the measures of the angles of a quadrilateral is 360 or four right angles. In the adjoining figure, WORK IS WORSHIP
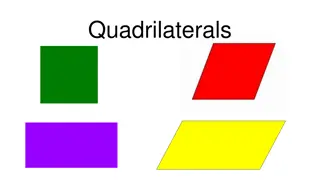
Types of quadrilaterals : Quadrilaterals are classified as : Square Rectangle Parallelogram Rhombus Trapezium Kite Trapezium : In Euclidean geometry, a convex quadrilateral with atleast one pair of parallel sides is called as a trapezium. In the adjoining diagram, ABCD is a trapezium in which AD || BC & AB and CD are two non-parallel sides. A trapezium is a quadrilateral having exactly one pair of opposite sides parallel. WORK IS WORSHIP
Kite : A quadrilateral in which two pairs of adjacent sides are equal is called a kite. In the adjoining quadrilateral, AB = BC & AD = CD, so ABCD is a kite. Properties : The diagonals of a kite intersect at right angles. In the figure, . The diagonal BD bisects as well as . The diagonal BD divides the kite into two congruent triangles. Here, . In the kite ABCD, . In the kite ABCD, OA = OC. The diagonal BD bisects the diagonal AC at O. Quadrilateral kites are used for kite flying. Its mainly is at the occasion of Makar Sankranti. It is celebrated widely in India. WORK IS WORSHIP
Parallelogram : A quadrilateral in which both pairs of opposite sides are parallel and equal is called a parallelogram. Its is symbolised as || gm. In the adjoining diagram, ABCD is a || gm. In a parallelogram, opposite sides are parallel and equal. AB || CD, AD || BC & AB = CD, AD = BC opposite angles are equal. consecutive interior angles or adjacent angles are supplementary. the diagonals are not equal but they bisect each other. each diagonal divides a parallelogram into two congruent triangles. two diagonals divides a || gm into four triangles of equal area. WORK IS WORSHIP
Properties of a parallelogram : Property 1 : Opposite angles of a parallelogram are equal. Proof : In the adjoining parallelogram ABCD, (Co.- interior angles)...... (i) (Co.- interior angles)...... (ii) Hence from (i) & (ii), Similarly, (Co.- interior angles)....(iii) Hence from (ii) & (iii), Therefore, opposite angles of a parallelogram are equal. WORK IS WORSHIP
Property 2 : Opposite sides of a parallelogram are equal. Proof : In the adjoining parallelogram ABCD, the diagonal AC divides it into two triangles. Therefore, in (alternate interior angles) (common side) (alternate interior angles) (ASA Congruence rule) AB = CD & BC = AD (C.P.C.T) Therefore opposite sides of a parallelogram are equal. Property 3 : Diagonals of a parallelogram bisect each other. Proof : In the adjoining parallelogram ABCD, the two diagonals AC & BD intersect each other at M, so that the parallelogram is divided into four triangles. Therefore, in WORK IS WORSHIP
(alternate interior angles) (opposite sides of a || gm) (alternate interior angles) (ASA congruence rule) MA = MC & MD = MB (C.P.C.T) Therefore, the diagonals of a || gm bisect each other. Property 4 : In a quadrilateral, if one pair of opposite sides is parallel and equal, then prove that it is a parallelogram. Proof : in the adjoining quadrilateral ABCD, the diagonal AC divides it into two triangles such That AB = CD & AB || CD. Therefore, in (opp. sides of a || gm.) (alt. int. angles) (common side) (SAS congruence rule) BC = AD (C.P.C.T) and (C.P.C.T) BC || CD (since a pair of alternate interior angles equal) Hence, ABCD is a parallelogram. WORK IS WORSHIP
Example 6 : ABCD is a parallelogram, BC is greater than CD by 3 cm. Find the measure of the lengths of sides BC and CD, if the perimeter of parallelogram is 70 cm. Solution : Let CD = x cm, then BC = x + 3 cm We know, AB = CD = x and AD = BC = x + 3 Perimeter = 70 cm x + x + 3 + x + x + 3 = 70 4x + 6 = 70 4x = 70 6 = 64 x = 16 AD = x + 3 = 16 + 3 = 19 cm Hence, BC = AD = 19 cm AB = CD = 16 cm Example 7 : Two adjacent angles of a parallelogram are 2 : 3. Find the measure of each its angles. Solution : Let ABCD be a parallelogram are its adjacent angles. [sum of adjacent angle = 180 ] {opp. sides of || gm} WORK IS WORSHIP
Let 2x + 3x = 180 5x = 180 Hence, , , [sum of adjacent angles = 180 ] Example 8 : In the adjoining figure, if ABCD & PQRS are parallelograms. Find the value of x. Solution : In || gm PQRS, (adjacent angles of a || gm) Now in || gm ABCD, (opp. of a || gm) x = 50 . WORK IS WORSHIP
TRY THESE : Worksheet 3 1. The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. find all the angles of the quadrilateral. 2. Three angles of a quadrilateral are 60 , 110 & 86 . Find the fourth angle of the quadrilateral. 3. In a parallelogram ABCD, if , find . 4. ABCD is a parallelogram in which and side AB is produced to point E as shown in the figure. Find (x + y). 5. ABCD is a trapezium with AB || DC, if then find all the angles of the trapezium. 6. In an isosceles trapezium ABCD with AB || DC, AD = BC & . Find all the angles of the trapezium. 7. Two adjacent sides of a parallelogram are in the ratio 2 : 3 & its perimeter is 70 cm. Find the length of the sides of the parallelogram. 8. ABCD is a trapezium in which and AB || CD. Find the values of x and y. NOTE : Every parallelogram is a trapezium but every trapezium is not a parallelogram. WORK IS WORSHIP
Rhombus : A parallelogram in which all the four sides are equal is called a rhombus. In the adjoining diagram, ABCD is a rhombus. In a rhombus, opposite sides are parallel and all the four sides are equal. AB || DC, BC || AD & AB = BC = CD = DA. the diagonals are not equal but they bisect each other at right angles. opposite angles are equal. the adjacent angles are supplementary. each diagonal divides it into two congruent triangles. two diagonals divide it into four congruent triangles. perimeter = 4 x side WORK IS WORSHIP
Properties of a rhombus : Property 1 : All the sides of a rhombus are equal. Proof : In the adjoining figure, ABCD is a rhombus. In , OA = OC (diagonals bisect each other) OB = OB (common side) (SAS Congruence rule) AB = BC (C.P.C.T)............. (i) Similarly, ............ (ii) ............ (iii) .............(iv) Hence from (i), (ii), (iii) & (iv), AB = BC = CD = DA. NOTE : Every rhombus is a parallelogram but every parallelogram is not a rhombus. WORK IS WORSHIP
Property 2 : The diagonals of a rhombus bisect each other at right angles. Proof : In the adjoining figure, ABCD is a rhombus. In , AB = BC (adjacent sides of a rhombus) OA = OC (diagonals bisect each other) OB = OB (common side) (SSS Congruence rule) (C.P.C.T) But (linear pair of angles). NOTE : If the diagonals of a parallelogram bisect each other at right angles, it is a rhombus. WORK IS WORSHIP
Example 9 : If the diagonals of a rhombus are of length 24 cm and 18 cm, find the length of the sides and hence its perimeter. Solution : In rhombus ABCD, let AC = 24 cm and BD = 18 cm In (pythagoras theorem) = 144 + 81 = 225 Since all the sides of a rhombus are equal, therefore AB = BC = CD = DA = 15cm Now, perimeter = 4 x side = 4 x 15 cm = 60 cm Example 10 : In the adjoining rhombus ABCD diagonals bisect each other at O. If , find (i) (ii) (iii) . Solution : Given, ABCD is a rhombus. (i) In (ASP of a ). WORK IS WORSHIP
(ii) As diagonal BD bisects (opposite angles are equal) (iii) (sum of a pair of co-interior angles) Example 11 : ABCD is a rhombus. If , then find . Solution : Let be . = (opp. angles of a rhombus) Now, in (ASP of a triangle) NOTE : Every parallelogram and rhombus is a trapezium but every trapezium is neither a parallelogram nor a rhombus. WORK IS WORSHIP
Rectangle : A quadrilateral in which opposite sides are equal and each interior angle is 90 is called a rectangle . In the adjoining figure, ABCD is a rectangle. Properties : In a rectangle, opposite sides are equal. AB = DC & AD = BC. opposite sides are parallel. AB || DC & AD || BC. each interior angle is a right angle. the diagonals are equal and bisect each other. AC = BD & OA = OC = OB = OD each diagonal divides it into two congruent triangles. NOTE : A parallelogram in which one angle is a right angle is called a rectangle. WORK IS WORSHIP
Square : A quadrilateral in which all the sides are equal and each interior angle is 90 is called a square. In the adjoining figure, ABCD is a square. Properties : In a square, all sides are equal. AB = BC = CD = DA. opposite sides are parallel. AB || DC & AD || BC. each interior angle is a right angle. the diagonals are equal and bisect each other at right angles. AC = BD, OA = OC, OB = OD & two diagonals divide it into four congruent triangles. NOTE : A parallelogram in which one pair of adjacent sides is equal and one of its angles is a right angle is called a square. Video (Activity) : https://youtu.be/rUNU83v8xAo WORK IS WORSHIP