Theory and Association of Attributes
Attributes are studied under Theory of Attributes and Association of Attributes. Theory of Attributes covers basic concepts like statistics of variables, while Statistics of Attributes deals with qualitative data that can't be measured quantitatively. Conditions and classifications with reference to attributes are also discussed, including dichotomy and arbitrary classifications.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
THEORY & ASSOCIATION 0F ATTRIBUTES
THEORY AND ASSOCIATION OF ATTRIBUTES Attributes are studied under the following two categories A) Theory of Attributes B) Association of Attributes
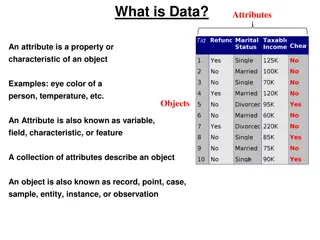
A) Theory of Attributes : Basic Concepts 1) ATTRIBUTES AND VARIABLES STATISTICS of VARIABLES: The observations where values can be measured numerically like: weight height, age , number of students etc are known as STATISTICS of VARIABLES
STATISTICS of ATTRIBUTES: The phenomena's which cannot be measured quantitatively, i.e Beauty, honesty, insanity, deafness etc, these observations can be grouped according to differences in quality. The observations possessing a particular quality, say , honesty are grouped together. thus the individuals possessing the quality (honesty) are counted and the qualitative data are given numerical shape, that is, they are quantified. These observations are grouped according to the presence or absence of a particular attribute and are called STATISTICS of ATTRIBUTES.
CONDITIONS WITH REFERENCE OF ATTRIBUTES An attribute requires the following conditions: The total number of objects of the same general class should be known. The characteristic should be readily identifiable preferably as the basis of an objective definition. The presence or absence of the attribute should be determine by an examination of the objects or situations. The number of objects which have the characteristic should be countable.
2) CLASSIFICATION WITH REFERENCE TO ATTRIBUTES Classification of data relating to attributes is made on the basis of the presence or absence of an attribute in the universe. Classification of data relating to attributes can be done in following ways: ARBITRARY OR VAGUE CLASSIFICATION COMBINATION OF ATTRIBUTES NOTATION AND TERMINOLOGY CLASS DICHOTOMY FREQUENCY
A) DICHOTOMY A classification of simple kind in which each class is divided into two sub classes is called division by DICHOTOMY or TWO FOLD classification. B) ARBITRARY OR VAGUE CLASSIFICATION Classification does not necessary imply existence of a clearly defined boundary between two classes. The division may be vague and uncertain. such type of a classification is called ARBITRARY or VAGUE classification. EX: Tall & Short, Sanity & Insanity.
C) NOTATION & TERMINOLOGY The capital letters A,B,C, are used to denote the presence of various attributes and the Greek letters , & are used to denote the absence of these attributes. Thus ( ) mean not (A), ( ) stands for not (B) and ( ) denotes not (C). NOTATIONS & TERMINOLOGY N PRESENCE OF ATTRIBUTE ABSENCE OF ATTRI BUTE A = Literacy = Illiteracy B = Smoking = Non Smoking C = Males = Females.
D) COMBINATION OF ATTRIBUTES Combinationof attributes is denoted by grouping together of the letters concerned e.g. AB is the combination of the attributes A & B. Thus if A stands for literacy and B for smoking then the combination will be in following manner: AB = COMBINATION OF ATTRIBUTES OF Literacy and Smoking. B = combination of attributes of ILLITERACY & SMOKING. A = Combination of attributes of LITERACY & NON SMOKING. = Combination OF attributes of ILLITERACY & NON SMOKING
E) CLASS FREQUENCY The number of observations falling in each class is its class frequency and is denoted by enclosing the corresponding class symbol in brackets like (A), ( ), (B), ( ), (AB), ( ) , (A ), ( B) etc. CLASS FREQUENCIES ( A) , (B ),(C y) Frequencies of Complementary events. (A) ,(AB), (ABC) Frequencies of positive Events. ( ), ( ) , ( y) Frequencies of negative events. (A ), ( B), (AB y) Frequencies of Mixed events.
CLASS FREQUENCY CLASS FREQUENCY is further divided into three parts: A) ORDER OF CLASSES & CLASS-FREQUENCIES B) TOTAL NUMBER OF CLASS FREQUENCIES C) ULTIMATE CLASS FREQUENCIES
B) ASSOCIATION OF ATTRIBUTES According to statistics two attributes A and B are associated only if they appear together in a greater number of cases than is to be expected if they are independent. EX: Two attributes A and B are associated: If (AB) (A) (B) N i.e. (AB) (A) (B) ( Positive association) N Or (AB) (A) (B) ( Negative association) N If (AB) = (A) (B) Then the two attributes A and B are independent. N
TYPES OF ASSOCIATION 1) Positive Association 2) Negative Association 3) Independence 4) Complete Association & Disassociation 5) Total &Partial Association 6) Illusory Association 7) Chance Association
1) POSITIVE ASSOCIATION Two attributes are said to be positive when they are present or absent together. EX: In a college the introduction of extra coaching leads to good results and this happens for number of years. Thus we can say extra coaching and good results have a positive association. 2) NEGATIVE ASSOCIATION When the two attributes are present alternatively, that is, if one is present the other is absent and if the other is present the former is absent.
3) INDEPENDENCE Absence of association means Independence. When two attributes do not have the tendency to be present together ,they are called Independence. 4) COMPLETE ASSOCIATION & DISASSOCIATION For finding out the association of two attributes as complete, two courses are open to us . Either we may say that for complete association all A s must be all B s and all B s must be A s . i.e. they both should be appear in equal numbers. Similarly complete Disassociation may take place when no A s are B s and no s are s or when either of these statements is true.
5) TOTAL OR PARTIAL ASSOCIATION Theassociation between two attributes in the whole universe is called total association . Partial association is also known as association in a sub universe. if two attributes A & B are associated with each other it is likely that this association may be due to the association of attributes A with C and attributes B with C. Thus association of A & B in the sub population C is known as Partial Association. 6) ILLUSORY ASSOCIATION The association which does not correspond to any real relationship between any two attributes is known as ILLUSORY ASSOCIATION.
7) CHANCE ASSOCIATION It must be remembered that association is not established by the fact that the observed value of (AB) is greater than or less than then the expected value of (AB). But it may also arise due to sampling fluctuations and may not be significant.
METHODS OF STUDYING ASSOCIATION Association refers to the relationship between two attributes. whether the two attributes are associated or not can be determined by the following methods: YULE S COEFFICIENT OF ASSOCIATION COEFFICIENT OF COLLIGATION COEFFICIENT OF CONTIGENCY PROBABILITY METHOD PROPORTION METHOD TSCHUPROW S COEFFICIENTS
1) PROBABILITY METHOD This method is based on the theory of probability for calculating the expected Frequencies of the attributes. EX: Expected frequency of (AB) = (A) (B) N In this method actually observed frequencies of attributes are compared with their expected frequencies. If actually observed frequencies are equal to the expected frequencies , the attributes are said to be independent. If the actually observed frequencies are greater than the expected frequencies, then the attributes are positively associated. LIMITATIONS: The main limitation of this method is that with the help of this method we can only find out the nature of association between the attributes ,whether the association between them is Positive , Negative or Independent. We cannot determine the degree of association.
2) PROPORTION METHOD If there is no relationship of any kind between two attributes A & B we expect to find the same proportion of A s among the B s , i.e. s , then these two attributes may be termed as independent. If the proportion of A s amongst the B s is greater than among the not B s ( or s) the two attributes A& B are positively associated. If the proportion of A s among B s is less than the among not B s ( or s) then the two attributes A and B are negatively associated. LIMITATIONS: This method can only determine the nature of association between attributes that is whether it is positive or negative or no association but it does not study the degree of association whether it is high or low.
3) YULES COEFFICIENT OF ASSOCIATION: In order to understand properly the significance of association or the relationship between two or more attributes ,it is necessary to find the degree of association between them. YULE S coefficient of association has the advantage of simplicity. If the attributes are independent of each other, the coefficient of association will be zero. If the attributes are perfectly or positively associated, the coefficient will be +1. If they are completely negatively associated or disassociated , the coefficient will be -1. thus the value of coefficient of association ranges from -1 to +1.
The degree of association is measured by the coefficient of association given by Prof. YULE is as follows: Q = (AB) ( ) ( A ) ( ) (AB) ( ) + (A ) ( ) Where : Q is coefficient of Association. CHARACTERISTIS OF YULE S COEFFICIENT OF ASSOCIATION 1) Q = +1 the association is positive and perfect. Q = - 1 the association is negative and perfect. Generally Q lies between +1 and -1. 2) Yule s coefficient is independent of the relative proportion of A s and s in the data. The value of the coefficient remains the same if all the terms containing A, , B, are multiplied by a constant. If Q = 0 there is no association.
4) COEFFICIENT OF COLLIGATION Prof. YULE has given another important coefficient which is also independent of the relative proportion of A s and s is known as coefficient of colligation and is denoted by (gamma) which can be calculated with the help of following formula: (AB) ( ) 1- (AB) ( ) = 1+ (AB) ( ) (AB) ( )
5) COEFFICIENT OF CONTINGENCY Format of Contingency Table: Contingency Table ATTRIBUTE A1 A2 A3 AS TOTAL - - B1 (A 1 B1) (A 2B1) (A 3B1 ) - - (A sB1) (B1) B2 (A 1B2) (A 2B2) (A 3B2) - - (A sB2) (B2) B3 (A 1B3) (A 2B3) (A 3B3) - - (A sB3) (B3) - - - - - - - - - - - - - - - - Bt (A 1Bt) (A 2Bt) (A 3Bt) -- - (A s B t ) (Bt) TOTAL (A1 ) (A2) (A3) - - (As) N
MAIN POINTS TO BE KEPT IN MIND ABOUT THE CONTINGENCY TABLE: 1) If attribute A is divided into S parts and the attribute B is divided into t parts, then there are (s t) cells in the table. 2) Each cell contains one ultimate class frequency. There are (s t) ultimate classes, the frequencies of which are denoted by (A 1B1), (A 1B2), (A 1Bt) etc. 3) The total of frequencies in a particular class is found as follows: (A1) = (A 1B1)+ (A 1B2)+(A 1B3)+ ..+(A 1Bt). (B2) = (A 1B1)+ (A 2B1)+(A 3B1)+ .+(A sB1). (As) = (A sB1)+ (A sB2)+ (A sB3)+ ..+ (A s Bt). 4) Total number of frequencies in the universe is equal to N. N = (A 1)+ (A 2)+ (A 3)+ ..(A s). Or N= (B 1)+ (B 2) + (B 3)+ ..(B t).
LIMITATIONS: The coefficient of contingency suffers from two serious defects: 1) It tells nothing about the nature of association , that is, whether association between A s and B s is positive or negative. 2) It increases with an increase in value of x2 towards a limit 1 but it never reaches that limit.
6) TSCHUPROWS COEFFICIENT To remedy the defects of coefficient of contingency mentioned above TSCHUPROW proposed the coefficient T defined by T2 = C2 (1 C2 ) (S -1) (t 1) This coefficient varies between 0 and 1 in the desired manner when s = t. T = C2 (1-C2 ) (S -1) (t 1)