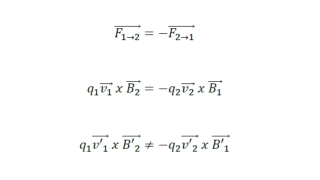The Theory of Relativity and Elementary Particles Study
The theory of relativity redefines our understanding of fields, particles, and their interactions. Explore how classical physics assumptions are challenged, and discover the implications of relativity on rigid bodies and rotating disks.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Elementary Particles in the theory of relativity Section 15
1. The field was first conceived by Faraday to explain action at a distance In classical physics, the field is a convenience for describing interactions between particles In relativity, due to the finite velocity of propagation of interactions, the field has physical reality. A particle creates a field around itself Then the field acts to produce a force on other particles located in this field. When the first particle moves, there is a time delay before other particles notice the change.
2. Classical theory of fields considers two types of field: gravitational and electromagnetic. This class deals only with the latter. 3. Before considering interactions between field and particle, the latter needs to be defined. 4. In classical physics, rigid non-deformable bodies are often assumed to represent particles, but relativity shows that this is only an approximation. Rigid bodies don t exist.
5. Assumption of rigidity leads to absurdity Consider a rotating disk, and suppose it to be rigid. Imagine a reference frame fixed to an infinitesimal element of the disk. This frame can be considered inertial during a moment. Different elements have different inertial frames in the given moment.
Consider line elements along a radius of the rotating disk The elements are perpendicular to their velocity No Lorentz contraction The total radius of the disk is the same as when it was at rest. v
Now consider line elements a long the circumference of the disk The assumption of rigidity means that the proper length of each element is the same as would be observed by a viewer at rest. However, an observer at rest sees that the length of each element is contracted. v
The circumference of the rotating disk is smaller than that of the disk at rest. Thus, due to rotation circumference/radius does not equal 2 This cannot be, unless the moving disk is no longer a disk, i.e. it must have deformed.
6. A different proof about the impossibility of rigid bodies. Apply an external force to one spot on an extended body. Speed of propagation of interactions is finite. Fext is not applied to all points simultaneously. Body must deform as it accelerates. Fext
7. Elementary particles are described completely by position r and velocity v. No independent motion of parts. Elementary particles cannot have finite dimensions. They are mathematical points.