Statistics and Epidemiology for the AKT Exam

The content covers essential topics in statistics and epidemiology for the AKT exam. It includes discussions on statistical terminology, calculations for evidence-based practice, graphical representations, and general advice for the exam. Key concepts such as the contingency table, null hypothesis, type 1 vs. type 2 errors, sensitivity, and specificity are explained with visual aids to enhance understanding and application in clinical decision-making.

• Statistics
• Epidemiology
• AKT Exam
• Evidence-Based Practice
• Clinical Decision Making

hduck Follow

Uploaded on Sep 30, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Some Statistics for the AKT

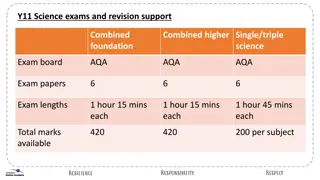
2. Section 2 of the AKT content guide Covers research, statistics and epidemiology. 10% of the exam This element is designed to examine the candidate s ability to use evidence and data to underpin clinical decision making, and the possession of critical appraisal skills sufficient to recognise good evidence and adopt guidelines as appropriate

3. What we are going to cover: Some statistical terminology (not all of it ) Calculations for evidence based practice Graphical representations General advice for the AKT

4. The contingency table True condition Positive Negative Positive True positive (TP) False positive (FP) Type 1 error Test condition Negative False negative (FN) Type 2 error True negative (TN)

5. The null hypothesis No relationship between two measured phenomena. Rejecting the null hypothesis leads to the conclusion that there is a relationship between the phenomena.

6. Type 1 vs Type 2 error

7. Sensitivity Measures the proportion of positive patients that are correctly identified as such. True condition Positive Negative Positive True positive (TP) False positive (FP) Type 1 error Test condition Negative False negative (FN) Type 2 error True negative (TN)

8. Sensitivity How would you calculate it? ?? Sensitivity = ??+?? True condition Positive Negative Positive True positive (TP) False positive (FP) Type 1 error Test condition Negative False negative (FN) Type 2 error True negative (TN)

9. Specificity Measures the proportion of negative patients that are correctly identified as such. True condition Positive Negative Positive True positive (TP) False positive (FP) Type 1 error Test condition Negative False negative (FN) Type 2 error True negative (TN)

10. Specificity How would you calculate it? ?? Specificity = ??+?? True condition Positive Negative Positive True positive (TP) False positive (FP) Type 1 error Test condition Negative False negative (FN) Type 2 error True negative (TN)

11. Positive predictive and negative predictive values Proportions of positive and negative values that are true positives and true negatives. True condition Positive Negative Positive True positive (TP) False positive (FP) Type 1 error Test condition Negative False negative (FN) Type 2 error True negative (TN)

12. PPV and NPV How would you calculate these? ?? PPV = ??+?? ?? ??+?? NPV = True condition Positive Negative Positive True positive (TP) False positive (FP) Type 1 error Test condition Negative False negative (FN) Type 2 error True negative (TN)

13. Example 400 plants are selected from a field. 75 of them have round leaves, the rest have pointy leaves. Scientists have developed a test to determine if a plant has round leaves or pointed leaves. 60 plants with round leaves were round positive. 20 plants with pointy leaves were round positive as well. Calculate the sensitivity, specificity, PPV and NPV of the test.

14. Step 1 Leaves Round Pointy Round positive Test Round negative

15. Step 1 Leaves Round Pointy Round positive 60 15 Test Round negative 20 305

16. Step 2 Plug in the numbers ?? 60+20=60 305 305+15=305 60 Sensitivity = 80= 75% ??+??= ?? ??+??= Specificity = 320= 95.3% Leaves Round Pointy Round positive 60 15 Test Round negative 20 305

17. Step 2 ?? 60+15= 60 305 305+20= 305 60 PPV = ??+??= ?? ??+??= 75= 80% NPV = 325= 93.8% Leaves Round Pointy Round positive 60 15 Test Round negative 20 305

18. Evidence Based Practice Experimental group (E) Control Group (C) Events (E) EE CE Non events (N) EN CN Total subjects (S) ES CS Event rate (ER) EER CER

19. Absolute Risk Reduction The change in the risk of an outcome of a given treatment/activity in relation to a comparison treatment/activity. Experimental group (E) Control Group (C) Events (E) EE CE Non events (N) EN CN Total subjects (S) ES CS Event rate (ER) EER CER

20. Absolute Risk Reduction ARR = EER-CER Experimental group (E) Control Group (C) Events (E) EE CE Non events (N) EN CN Total subjects (S) ES CS EER=?? CER=?? Event rate (ER) ?? ??

21. Number Needed to Treat The average number of patients who need to be treated to prevent one additional bad outcome Experimental group (E) Control Group (C) Events (E) EE CE Non events (N) EN CN Total subjects (S) ES CS Event rate (ER) EER CER

22. Number Needed to Treat 1 NNT = ??? ??? Experimental group (E) Control Group (C) Events (E) EE CE Non events (N) EN CN Total subjects (S) ES CS Event rate (ER) EER CER

23. Number Needed to Treat For example a drug will treat a disease. PA is the probability the drug will treat the disease. PBis the probability the group still have the disease.

24. Number Needed to Treat Description PA PB NNT Interpretation Everybody is cured with the pill; nobody without Perfect drug 0.0 1.0 1.0 Ten take the pill; 8 cured by the pill, 1 cured by itself, 1 still sick. Ten take the pill; 4 cured by the pill, 3 cured by itself, 3 still sick. Ten take the pill; 6 cured but 5 of those would be cured anyway. Ten take the pill, one is cured by the pill, one cured by itself, 8 still have the disease. Ten take the pill and 9 are cured; but 8 would have been cured anyway. Ten take the pill, two would have been cured without it, but with the pill, only one is cured, so NNH=10. Very good drug 0.1 0.9 1.25 Satisfactory drug 0.3 0.7 2.5 High placebo effect 0.4 0.5 10 Low cure rate 0.8 0.9 10 Goes away by itself 0.1 0.2 10 Sabotages cure 0.9 0.8 10

25. Relative Risk The probability of an event occurring in an exposed group to the probability occurring in a non exposed group. Experimental group (E) Control Group (C) Events (E) EE CE Non events (N) EN CN Total subjects (S) ES CS Event rate (ER) EER CER

26. Relative Risk Relative Risk = ??? ??? Experimental group (E) Control Group (C) Events (E) EE CE Non events (N) EN CN Total subjects (S) ES CS Event rate (ER) EER CER

27. Odds Ratios A measure of association between an exposure and an outcome Experimental group (E) Control Group (C) Events (E) EE CE Non events (N) EN CN Total subjects (S) ES CS Event rate (ER) EER CER

28. Odds Ratios ?? ?? ?? ?? OR= Experimental group (E) Control Group (C) Events (E) EE CE Non events (N) EN CN Total subjects (S) ES CS Event rate (ER) EER CER

29. Example 200 rabbits are randomly allocated to two groups. They have all been exposed to a virus. 100 of the rabbits are given the treatment . 95 rabbits are cured. Of the 100 rabbits given a placebo, 10 are cured. Calculate the ARR, NNT, Relative risk and odds ratios.

30. Step 1 Experimental group (E) Control Group (C) Events (E) Non events (N) Total subjects (S) Event rate (ER)

31. Step 1 Experimental group (E) Control Group (C) Events (E) 95 10 Non events (N) 5 90 Total subjects (S) 100 100 Event rate (ER) 0.95 0.1

32. Step 2 How would you calculate ARR? ARR = EER-CER = 0.85=85% Experimental group (E) Control Group (C) Events (E) 95 10 Non events (N) 5 90 Total subjects (S) 100 100 Event rate (ER) 0.95 0.1

33. Step 2 How would you calculate NNT? 1 1 NNT = 0.85= 1.17 ??? ???= Experimental group (E) Control Group (C) Events (E) 95 10 Non events (N) 5 90 Total subjects (S) 100 100 Event rate (ER) 0.95 0.1

34. Step 2 How would you calculate relative risk? Relative Risk = ??? ???= 0.95 0.1= 9.5 Experimental group (E) Control Group (C) Events (E) 95 10 Non events (N) 5 90 Total subjects (S) 100 100 Event rate (ER) 0.95 0.1

35. Step 2 How would you calculate odds ratios? 95 5 10 90 ?? ?? ?? ?? = 19 0.11=171 OR= = Experimental group (E) Control Group (C) Events (E) 95 10 Non events (N) 5 90 Total subjects (S) 100 100 Event rate (ER) 0.95 0.1

36. Graphical Representations

37. Normal distribution

38. Skewed distribution

39. Scatter diagrams

40. Box plots

41. Forest plots

42. Funnel plots http://www.bmj.com/content/343/bmj.d4002

43. Cates diagrams

44. Kaplan Meier curves

45. Conclusion We covered some terminology and calculations involved in the AKT We also covered some diagrams and the interpretation of these diagrams

46. What else should I do? Go over section 2 of the AKT content guide. Do lots of practice questions. Learn the statistical terminology (59+ terms) Understand the principles of screening

47. What about the administration section? Oxford Handbook of GP first few chapters tells you most of what you need to know about section 3.

48. Learn (this is not an exhaustive list): - DVLA fitness to drive guidelines, - CAA fitness to fly guidelines, - Childhood imms schedule, - School exclusion guidelines, - Child development milestones, - UKMEC guidelines, - Emergency management, - Consultation models, - Any relevant CKS/NICE guidelines of common conditions.

49. Questions? Ideas? Concerns?? Expectations???