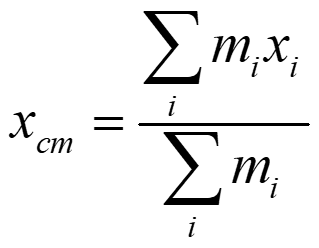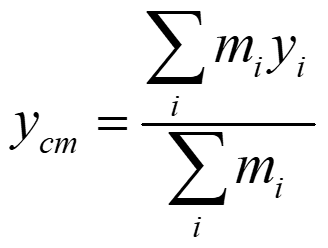Static Equilibrium: Center of Mass and Gravity
Chapter 9: Static Equilibrium;
Elasticity and Fracture
•
Things that we don’t want to move or accelerate
(neither linearly nor angularly)
•
A more realistic treatment of real materials
•
First, some terminology
1
Center of Mass versus Center of Gravity
Center of Mass: The mass-weighted average position
of all the particles that make up the system
CM
2
Center of Mass versus Center of Gravity
Center of Gravity: The single point at which the
collective
force of gravity can be said to act.
3
Center of Mass versus Center of Gravity
Center of Gravity: The single point at which the
collective
force of gravity can be said to act.
CoG
4
Bird Toy
5
6
Center of Mass versus Center of Gravity
Center of Gravity: The single point at which the
collective
force of gravity can be said to act.
CoG
In principle,
the CoG is
not the same
as the CoM
7
8
CoG
CoM
In principle,
the CoG is
not the same
as the CoM
9
Center of gravity
An example in which the center of gravity
does not
coincide with the center of mass
Petronas Towers, Malaysia
451.9 meters tall
g at top, bottom
differ by 0.014%
The center of gravity
is 2cm below the
center of mass
1482.6 feet
10
To support or suspend an object at a single point,
the center of gravity must be directly above or below
the point of support/suspension.
Center of
gravity
So what?
11
For an object supported at several points:
The center of gravity must be within the area
bounded by the supports
OK
NOT OK
12
Tipping over a refrigerator
13
Stable and unstable equilibria
14
Stable and unstable equilibria
Stable equilibrium
: After a small displacement,
the object returns to the equilibrium
15
Stable and unstable equilibria
Unstable equilibrium
: After a small displacement,
the object goes away from the equilibrium
16
Review how to calculate torque
17
Torque
Units: meter-Newton
…but these are
not
Joules!
1. The “F perpendicular” method
18
Torque
2. The “lever arm” or “moment arm” method
19
The conditions for static equilibrium
20
Example 5.3: two-dimensional equilibrium
Engine’s weight is
We have already done a static problem using
21
Some example static equilibrium problems
that involve the torque condition
22
STATIC EQUILIBRIUM
23
NOT IN STATIC EQUILIBRIUM
24
NOT IN STATIC EQUILIBRIUM
(But not about
every
axis!)
25
Both
must be satisfied for static equilibrium!
The conditions for static equilibrium
26
Static Equilibrium Concept Questions
27
28
29
30
31
A 1 kg ball is hung at the end of a rod 1 m
long. If the system balances at a point on
the rod 0.25 m from the end holding the
mass, what is the mass of the rod?
a
)
1
/
4
k
g
b
)
1
/
2
k
g
c
)
1
k
g
d
)
2
k
g
e
)
4
k
g
32
A 1 kg ball is hung at the end of a rod 1 m
long. If the system balances at a point on
the rod 0.25 m from the end holding the
mass, what is the mass of the rod?
a
)
1
/
4
k
g
b
)
1
/
2
k
g
c
)
1
k
g
d
)
2
k
g
e
)
4
k
g
33
A 1 kg ball is hung at the end of a rod 1 m
long. If the system balances at a point on
the rod 0.25 m from the end holding the
mass, what is the mass of the rod?
a
)
1
/
4
k
g
b
)
1
/
2
k
g
c
)
1
k
g
d
)
2
k
g
e
)
4
k
g
The total torque about the pivot
The total torque about the pivot
must be zero!
must be zero!
The CM of the
rod is at its center,
0.25 m to the
0.25 m to the
right of the pivot
right of the pivot
. Since this
must balance the ball, which is
the
same distance to the left of
same distance to the left of
the pivot
the pivot
, the masses must be
the same !
34
Static equilibrium examples
35
A (static) mobile hangs as
shown below. The rods are
massless and have lengths as
indicated. The mass of the ball
at the bottom right is
1 kg
.
What is the total mass of the
mobile?
a
)
5
k
g
b
)
6
k
g
c
)
7
k
g
d
)
8
k
g
e
)
9
k
g
36
a
)
5
k
g
b
)
6
k
g
c
)
7
k
g
d
)
8
k
g
e
)
9
k
g
Use torques in two steps: (1) find
the big mass on the bottom left
(lower rod only). (2) use the entire
lower rod assembly (with two
masses) to find the mass on top right.
Finally, add up all the masses.
Finally, add up all the masses.
A (static) mobile hangs as
shown below. The rods are
massless and have lengths as
indicated. The mass of the ball
at the bottom right is
1 kg
.
What is the total mass of the
mobile?
37
a
)
5
k
g
b
)
6
k
g
c
)
7
k
g
d
)
8
k
g
e
)
9
k
g
A (static) mobile hangs as
shown below. The rods are
massless and have lengths as
indicated. The mass of the ball
at the bottom right is
1 kg
.
What is the total mass of the
mobile?
Use torques in two steps: (1) find
the big mass on the bottom left
(lower rod only). (2) use the entire
lower rod assembly (with two
masses) to find the mass on top right.
Finally, add up all the masses.
Finally, add up all the masses.
38
Balance!
39
40
Balance!
41
Balance!
42
Sum of the masses: (2 + 3 + 1) kg = 6 kg
43
44
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown.
(a)
Find the tension in the supporting wire (at 35.0
∘
)
(b)
Find the horizontal force exerted by the hinge on the beam at the wall.
(c)
Find the vertical force exerted by the hinge on the beam at the wall.
0.85m
1.35m
1.70m
45
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown.
(a)
Find the tension in the supporting wire (at 35.0
∘
)
(b)
Find the horizontal force exerted by the hinge on the beam at the wall.
(c)
Find the vertical force exerted by the hinge on the beam at the wall.
Note the
coordinate system
Horizontal direction
Vertical direction
46
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown.
(a)
Find the tension in the supporting wire (at 35.0
∘
)
(b)
Find the horizontal force exerted by the hinge on the beam at the wall.
(c)
Find the vertical force exerted by the hinge on the beam at the wall.
0.85m
1.35m
1.70m
Now do the torques
47
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown.
(a)
Find the tension in the supporting wire (at 35.0
∘
)
(b)
Find the horizontal force exerted by the hinge on the beam at the wall.
(c)
Find the vertical force exerted by the hinge on the beam at the wall.
0.85m
1.35m
1.70m
Solve for T
48
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown.
(a)
Find the tension in the supporting wire (at 35.0
∘
)
(b)
Find the horizontal force exerted by the hinge on the beam at the wall.
(c)
Find the vertical force exerted by the hinge on the beam at the wall.
0.85m
1.35m
1.70m
Recall that from
we got
49
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown.
(a)
Find the tension in the supporting wire (at 35.0
∘
)
(b)
Find the horizontal force exerted by the hinge on the beam at the wall.
(c)
Find the vertical force exerted by the hinge on the beam at the wall.
0.85m
1.35m
1.70m
Recall that from
we also got
The negative sign means that my initial
guess about the direction of this force
was wrong!
50
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown.
(a)
Find the tension in the supporting wire (at 35.0
∘
)
(b)
Find the horizontal force exerted by the hinge on the beam at the wall.
(c)
Find the vertical force exerted by the hinge on the beam at the wall.
The vertical hinge force is
actually like this
upwards
to the right
as shown
51
Elasticity and Fracture
52
Discussed statics: conditions for equilibrium
We have been assuming perfectly rigid objects
But how do real materials respond to applied forces?
Need to know this if you’re going to build stuff
like buildings or bridges
53
54
55
Stress
What you do to something
56
Strain
How it responds
57
(Stress) = E (Strain)
= a property of the material
E = Elastic modulus or Young’s modulus
58
The larger E is, the stiffer the material is
59
Units
60
Table on page 242
61
Example
A 9.5 m steel rod has a cross-sectional area
of 0.15 m
2.
A sign of mass 2000 kg is
attached to it.
Sign
Rod radius is about 22 cm
62
Example
A 9.5 m steel rod has a cross-sectional area
of 0.15 m
2.
A sign of mass 2000 kg is
attached to it.
(a) What is the stress?
Tensile stress =
Sign
Tensile stress =
63
Example
A 9.5 m steel rod has a cross-sectional area
of 0.15 m
2.
A sign of mass 2000 kg is
attached to it.
(b) What is the strain?
Sign
64
Example
A 9.5 m steel rod has a cross-sectional area
of 0.15 m
2.
A sign of mass 2000 kg is
attached to it.
(c) How much does the rod stretch?
Sign
65
66
Shear stress and strain
67
Shear stress and strain
G = Shear modulus
68
69
Volume change: Bulk modulus
B = Bulk modulus
70
71
Fracture:
If there’s too much stress, it breaks
72
Fracture:
If there’s too much stress, it breaks
Table showing the maximum stress (F/A) materials can sustain
73
What you should know
E = Elastic modulus or
Young’s modulus
Tension and compression
Shear
G = Shear modulus
B = Bulk modulus
Bulk
The idea of the ultimate strength of materials
74
THE END
75
In this chapter, you will delve into the concepts of center of mass and center of gravity. Explore the differences between these fundamental points and learn how they affect the equilibrium of objects. Discover why the center of gravity may not always align with the center of mass through real-world examples like the Petronas Towers in Malaysia.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Chapter 9: Static Equilibrium; Elasticity and Fracture Things that we don t want to move or accelerate (neither linearly nor angularly) A more realistic treatment of real materials First, some terminology 1
Center of Mass versus Center of Gravity Center of Mass: The mass-weighted average position of all the particles that make up the system y CM x = = m x m y + + m x m x + m x m i i i i = 1 1 2 2 m 3 3 i y i x + cm cm m m m 1 2 3 i i i i 2
Center of Mass versus Center of Gravity Center of Gravity: The single point at which the collective force of gravity can be said to act. 3
Center of Mass versus Center of Gravity Center of Gravity: The single point at which the collective force of gravity can be said to act. CoG 4
Bird Toy 5
Center of Mass versus Center of Gravity Center of Gravity: The single point at which the collective force of gravity can be said to act. In principle, the CoG is not the same as the CoM CoG g If has the same value at all points, then the center of gravity coincides with the center of mass 7
What happens if does not have the same value at all points? g 8
What if does not have the same value at all points? g In principle, the CoG is not the same as the CoM CoM CoG 9
Center of gravity An example in which the center of gravity does not coincide with the center of mass Petronas Towers, Malaysia 451.9 meters tall 1482.6 feet g at top, bottom differ by 0.014% The center of gravity is 2cm below the center of mass 10
So what? To support or suspend an object at a single point, the center of gravity must be directly above or below the point of support/suspension. Center of gravity 11
For an object supported at several points: The center of gravity must be within the area bounded by the supports OK NOT OK 12
Stable and unstable equilibria Stable equilibrium: After a small displacement, the object returns to the equilibrium 15
Stable and unstable equilibria Unstable equilibrium: After a small displacement, the object goes away from the equilibrium 16
Torque 1. The F perpendicular method = RF R and points to where the force acts. is a vector that starts at the axis of rotation F F F R Units: meter-Newton but these are not Joules! 18
Torque 2. The lever arm or moment arm method = R F F R R 19
The conditions for static equilibrium = 0 = 0 F net net about any axis 20
= 0 F We have already done a static problem using net Example 5.3: two-dimensional equilibrium w = 1777.7 N Engine s weight is Find the three tensions in the chains in terms ofw 21
Some example static equilibrium problems that involve the torque condition 22
= 0 F net = 0 net STATIC EQUILIBRIUM 23
= 0 F net = 0 net NOT IN STATIC EQUILIBRIUM 24
= 0 F net = 0 net (But not about every axis!) NOT IN STATIC EQUILIBRIUM 25
The conditions for static equilibrium = 0 = 0 F net net about any axis Both must be satisfied for static equilibrium! 26
a) 1/4 kg A 1 kg ball is hung at the end of a rod 1 m b) 1/2 kg long. If the system balances at a point on c) 1 kg the rod 0.25 m from the end holding the d) 2 kg mass, what is the mass of the rod? e) 4 kg 1m 1kg 32
a) 1/4 kg A 1 kg ball is hung at the end of a rod 1 m b) 1/2 kg long. If the system balances at a point on c) 1 kg the rod 0.25 m from the end holding the d) 2 kg mass, what is the mass of the rod? e) 4 kg 1m 1kg 33
a) 1/4 kg A 1 kg ball is hung at the end of a rod 1 m b) 1/2 kg long. If the system balances at a point on c) 1 kg the rod 0.25 m from the end holding the d) 2 kg mass, what is the mass of the rod? e) 4 kg The total torque about the pivot must be zero! The CM of the mROD = 1 kg same distance rod is at its center, 0.25 m to the right of the pivot. Since this X must balance the ball, which is CM of rod 1 kg the same distance to the left of the pivot, the masses must be the same ! 34
A (static) mobile hangs as shown below. The rods are massless and have lengths as indicated. The mass of the ball at the bottom right is 1 kg. What is the total mass of the mobile? a) 5 kg b) 6 kg c) 7 kg d) 8 kg e) 9 kg ? 1 m 2 m ? 1 kg 1 m 3 m 36
A (static) mobile hangs as shown below. The rods are massless and have lengths as indicated. The mass of the ball at the bottom right is 1 kg. What is the total mass of the mobile? a) 5 kg b) 6 kg c) 7 kg d) 8 kg e) 9 kg Use torques in two steps: (1) find ? the big mass on the bottom left 1 m 2 m (lower rod only). (2) use the entire lower rod assembly (with two ? 1 kg masses) to find the mass on top right. Finally, add up all the masses. 1 m 3 m 37
A (static) mobile hangs as shown below. The rods are massless and have lengths as indicated. The mass of the ball at the bottom right is 1 kg. What is the total mass of the mobile? a) 5 kg b) 6 kg c) 7 kg d) 8 kg e) 9 kg Use torques in two steps: (1) find ? the big mass on the bottom left 1 m 2 m (lower rod only). (2) use the entire lower rod assembly (with two ? 1 kg masses) to find the mass on top right. Finally, add up all the masses. 1 m 3 m 38
? 1 m 2 m ? 1 kg (1kg)g 1 m 3 m ( kg) x g = (3m)(1kg) g R = (1m)( kg) x g L Balance! = (1m)( kg) (3m)(1kg) x g g x = 3 39
? 1 m 2 m 3 kg 1 kg 1 m 3 m 40
? 1 m 2 m ( kg) x g (4 kg)g = (1m)(4 kg) g = (2 m)( kg) x g L R Balance! = (1m)(4 kg) (2 m)( kg) g x g = 2 x 41
2 kg 1 m 2 m ( kg) x g (4 kg)g = (1m)(4 kg) g = (2 m)( kg) x g L R Balance! = (1m)(4 kg) (2 m)( kg) g x g = 2 x 42
2 kg 1 m 2 m 3 kg 1 kg 1 m 3 m Sum of the masses: (2 + 3 + 1) kg = 6 kg 43
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown. (a) Find the tension in the supporting wire (at 35.0 ) (b) Find the horizontal force exerted by the hinge on the beam at the wall. (c) Find the vertical force exerted by the hinge on the beam at the wall. T h F 35o vF 170 N 215 N 0.85m 1.35m 1.70m 45
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown. (a) Find the tension in the supporting wire (at 35.0 ) (b) Find the horizontal force exerted by the hinge on the beam at the wall. (c) Find the vertical force exerted by the hinge on the beam at the wall. Note the + = 0 F net coordinate system T h F + 35o Horizontal direction ( ) = o cos 35 0 h F T vF 170 N 215 N Vertical direction ( ) ( ) ( ) + = o 170 N 215 N sin 35 0 vF T ( ) ( ) = o sin 35 385 N vF T 46
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown. (a) Find the tension in the supporting wire (at 35.0 ) (b) Find the horizontal force exerted by the hinge on the beam at the wall. (c) Find the vertical force exerted by the hinge on the beam at the wall. + + T h F + 35o vF 170 N 215 N 0.85m 1.35m Now do the torques 1.70m 47
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown. (a) Find the tension in the supporting wire (at 35.0 ) (b) Find the horizontal force exerted by the hinge on the beam at the wall. (c) Find the vertical force exerted by the hinge on the beam at the wall. + = 0 + net T ( ( ( )( ) T ) h F + 35o 0.85m 170 N ( ) + sin 35o 1.35m vF 170 N )( ) = 0 1.7 m 215 N 215 N 0.85m Solve for T 1.35m ( )( ( ) ( ) )( ) ) + 0.85m 170 N 1.7 m 215 N = T ( 1.35m sin 35o 1.70m T = 658.6 N 48
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown. (a) Find the tension in the supporting wire (at 35.0 ) (b) Find the horizontal force exerted by the hinge on the beam at the wall. (c) Find the vertical force exerted by the hinge on the beam at the wall. = 0 F + Recall that from we got net ( + T ) = o cos 35 0 h F T h F + 35o ( ) = cos 35o h F T vF ( ) 170 N ( ) h F = 658.6 N cos 35o 215 N 0.85m h F = 539.5 N 1.35m 1.70m 49
9.18: A shop sign weighing 215N hangs from the end of a uniform 170-N beam as shown. (a) Find the tension in the supporting wire (at 35.0 ) (b) Find the horizontal force exerted by the hinge on the beam at the wall. (c) Find the vertical force exerted by the hinge on the beam at the wall. = 0 F + Recall that from we also got net + T ( ) ( ) = o sin 35 385 N vF T h F + 35o ( ) ( ( ) ) vF = o 658.6 N sin 35 385 N vF 170 N vF = 215 N 7.2 N 0.85m The negative sign means that my initial guess about the direction of this force was wrong! 1.35m 1.70m 50
