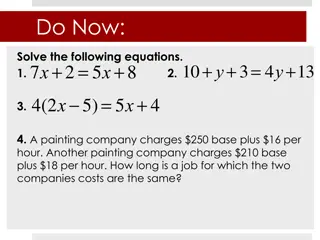Solving Rational Equations Review

Slide Note

Explore solving rational equations involving variables and find the lowest common denominator. Identify errors in problem-solving steps and determine the correctness of solutions between multiple students. Practice steps for solving complex equations with detailed explanations and images.

daum183 Follow

Uploaded on Mar 08, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

Download Presentation

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

E N D

Presentation Transcript

CH6 Review Solving Rational Equations

When solving this equation, what is the Lowest Common Denominator? ) 3 a x 2 ) 9 b x ( )( ) 2 2 ) 3 9 c x x ( ) )( 2 ) 3 d x ( ) + ) 3 3 e x x

When solving this equation, what is the Lowest Common Denominator? ) 3 a x ) 4 b x + 2 ) 7 12 c x x )( ) ( )( )( + 2 ) 3 4 7 12 d x x x x ) ( + 2 ) 4 7 12 e x x x

When solving the following equation, which steps have errors? Solve for y: a) Step 1: The mistake is that the LCD is not equal to y but should be 2y Step 1: Find the LCD: y b) Step 2: The mistake in step 2 is that you forgot to multiply one of the terms by the LCD and NOT just the terms with a denominator 3 y 1 y ( ) y ( ) y = + 2 Step 2: Multiply all steps by y 3 y 1 y ( ) y ( ) y c) Step 3: you are not supposed to cancel the denominator when solving for x = + 2 Step 3: Cancel all the denominators d) Step 4: Since all the variables are gone, this is an error 2 1 = + 3 Step 4: Combine Like Terms = 3 3 Step 5: Solve for x e) There is no error since the answer at the very end is correct

The work below are the steps provided by two students when solving the equation shown. Which student is correct? 2 x Student 1 x Student a) Student 1 is correct because his work required less steps x x x x = 5 x 5 x 5 x 5 x = 1: s x = 1: s x b) Student 1 is correct because he/she simplified the expression correctly 5 x 5 x c) Student 2 is correct because their work is more detailed and required more steps = = 2: 2: s x s x 5 5 = 3: s x = 3: 1 s x d) Student 2 is correct because he/she simplified the expression correctly = 4: s x e) Both students are correct because they both have the same answer 5: 1 s x

When solving this equation, which of the following is not a valid first step? a) Move the (2/x) to the right side to combine like terms b) Multiply all three terms by the LCD x c) Multiply all three terms by the LCD 3x d) Multiply all three terms by a common denominator of 3x2 e) Guess and check a bunch of different values for x so that both sides will be equal

When solving the following equation, which of the following is incorrect? a) Move the 16 to the right side and then square root both sides to solve for t 1 1: 16 s t b) Factor the left side of the equation by using the difference of squares formula 1 1 1: 4 4 s t t = + = 0 2 1 t 1 t 1 t = 2: 4 s = = 2: 4 4 s or c) Square root the left side of the equation and then solve for x algebraically d) Multiply all terms by t2 to cancel out all denominators and then solve for x 1 t ( ) t ( ) t ( ) t 1 t = 2 2 2 16 0 = 1: s 16 0 2 2 1 16 = 2 0 t 1 t = 2: 4 0 s

Solve for x:

Q: Indicate True or False for each of the statements below: 1) When Multiplying Rational functions, you must have a common denominator True or FALSE 2) When Adding/Subtracting Rational functions, you must have a common denominator True or FALSE 3) When solving Rational Functions, you must have a common denominator True or FALSE

Add the following: 1 2 2 x + 1 + = x 4 )4 a 2 x 4 ) b 2 4 x 2 x x x )4 c 2 2 ) d 2 4 x

Subtract the following: 3 2 1 2 n n = 8 4 n n ) ) a b ( )( ) ( )( ) 1 2 1 2 n n n 5 1 4 5 1 8 n n ) ) c d ( )( ) ( )( ) 2 2 n n n n

Add the following: y x y y 2 x + = 2 2 x ) 1 )1 a b + 2 y x y y x x ) ) c d 2 2 x y

The following work was shown in solving the equation below. AT which step was the first mistake made? a) The first mistake is in step 1 k + 2 1 3 4 4 k k k k b) The first mistake is in step 2 ( ) 1 = 1: s 4 4 4 k k k k + 2 1 3 4 4 k k k k c) The first mistake is in step 4 because terms were incorrectly cancelled out ( ) 1 = 2: 4 4 4 s k k k k ) ( ) ( ) ( d) The first mistake is in step 7 because one of the answer is extraneous + = 2 3: 1 4 4 3 4 s k k k + = + + 2 4:4 4 4 3 4 s k k k k e) There are no mistakes in all the steps and both answers are correct = + 2 5:0 3 s k ( k ) ( = + ) or 6:0 3 s k k ( ) = = 7: 0 3 s k k

The following work was shown in solving the equation below. AT which step was the first mistake made? a) The first mistake is in step 1, you can t move an entire rational expr. to the opposite side + + 2 3 18 3 10 x x x x = 1: 2 s 12 x b) The first mistake is in step 3 + 2 10 2 x + + 2 3 18 1 + 3 x x x c) The first mistake is in step 4 = 2: 2 12 s x 2 0 x + 2 d) The first mistake is in step 5 because you can not cancel the binomials 2 15 x x = 3: 2 12 s x + 2 10 x ( )( ) ) ( 5 e) The first mistake is in steps 7 because x=-5 is not included as one of the answers + = + 2 4: 2 12 2 ( x 10 2 15 s x x x x )( )( ) + = + 5: 4 6 5 3 s x x x f) There are no mistakes and all the steps are correct = 6:4 24 3 s x x x = 7: 7 s