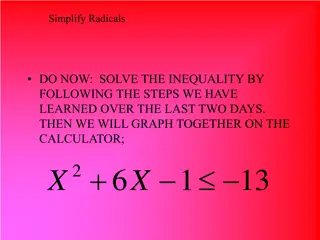Solving Equations with Exponents and Radicals
Radicals and nth roots
Solving equations with exponents
and radicals
But first, some Domain and range review.
Find the domain
and range of the
blue
graph
Find the domain and range
of the
pink
graph
State the domain and range of the function in the red
SOLUTION
Domain:
x
0
, Range:
y
0
Domain and range: all real numbers
Objectives/Assignment
•
Change between radical and exponent
notation
•
Evaluate nth roots of real numbers using both
radical notation and rational exponent
notation.
•
Use nth roots to solve equations containing
radicals and exponents other than 1 or 2.
Ex. 5: Using nth Roots in “Real Life”
•
T
h
e
t
o
t
a
l
m
a
s
s
M
(
i
n
k
i
l
o
g
r
a
m
s
)
o
f
a
s
p
a
c
e
c
r
a
f
t
t
h
a
t
c
a
n
b
e
p
r
o
p
e
l
l
e
d
b
y
a
m
a
g
n
e
t
i
c
s
a
i
l
i
s
,
i
n
t
h
e
o
r
y
,
g
i
v
e
n
b
y
:
where m is the mass (in kilograms) of the magnetic
sail, f is the drag force (in newtons) of the
spacecraft, and d is the distance (in astronomical
units) to the sun. Find the total mass of a
spacecraft that can be sent to Mars using m = 5,000
kg, f = 4.52 N, and d = 1.52 AU
.
Solution
The spacecraft can have a total mass of about 47,500
kilograms. (For comparison, the liftoff weight for a space
shuttle is usually about 2,040,000 kilograms.
Ex. 6: Solving an Equation Using an nth Root
•
NAUTICAL SCIENCE. The
Olympias
is a
reconstruction of a trireme, a type of Greek
galley ship used over 2,000 years ago. The power
P (in kilowatts) needed to propel the
Olympias
at
a desired speed, s (in knots) can be modeled by
this equation:
P = 0.0289s
3
A volunteer crew of the
Olympias
was able to
generate a maximum power of about 10.5
kilowatts. What was their greatest speed?
SOLUTION
•
The greatest speed attained by the
Olympias
was
approximately 7 knots (about 8 miles per hour).
Solve the equation. Check for extraneous solutions.
check your solutions!!
check your solutions!!
Goal
Goal
1
1
Solve equations that contain
square roots
Ex.1)
Key Step:
To raise each side of
the equation to the
same power.
6.6 Solving Radical Equations
6.6 Solving Radical Equations
Simple Radical
6.6 Solving Radical Equations
6.6 Solving Radical Equations
One Radical
Ex.3)
Don’t forget to
Don’t forget to
check your
check your
solutions!!
solutions!!
6.6 Solving Radical Equations
6.6 Solving Radical Equations
Don’t forget to
Don’t forget to
check your
check your
solutions!!
solutions!!
Radicals with an Extraneous Solution
Ex.5)
6.6 Solving Radical Equations
6.6 Solving Radical Equations
Two Radicals
Ex.4)
Don’t forget to
Don’t forget to
check your
check your
solutions!!
solutions!!
Steps for two
radical equations
•
Set radical equal
to radical
•
Square both
sides
•
Solve for x
Without solving, explain why
6.6 Solving Radical Equations
6.6 Solving Radical Equations
has no solution.
Radical notation
Index
Number
Radicand
Radical
The index number becomes the
denominator of the exponent.
n
> 1
More on Radicals
•
If n is odd
a
can be any number
•
If
n
is even, then
a
must be a positive
number or zero, otherwise there is no
real solution.
Example: Radical form to Exponential
Form
Change to exponential form.
or
or
Example: Exponential to Radical Form
Change to radical form.
The denominator of the
exponent becomes the index
number of the radical
.
6.1 nth Roots and Rational Exponents
6.1 nth Roots and Rational Exponents
Using Rational Exponent Notation
Rewrite the expression using RADICAL notation.
Ex)
Ex)
Ex. 2 Evaluating Expressions with
Rational Exponents
A.
B.
Using radical notation
Using rational exponent
notation.
OR
OR
E
v
a
l
u
a
t
e
b
o
t
h
w
a
y
s
(
a
)
p
r
o
f
i
c
i
e
n
t
1
6
3
/
2
a
n
d
(
b
)
a
d
v
a
n
c
e
d
3
2
–
3
/
5
.
S
O
L
U
T
I
O
N
Rational Exponent Form
Radical Form
a
.
1
6
3
/
2
16
3/2
b
.
3
2
–
3
/
5
32
-3/5
Cancelling radicals to solve equations
a.
b.
c.
d.
6.6 Solving Radical Equations
6.6 Solving Radical Equations
Ex.2)
Key Step:
Before raising each side
to the same power, you
should
isolate
isolate
the
radical expression
on
one side of the
equation.
Equations with “nth root” radicals
Don’t
forget to
check it.
6.1 nth Roots and Rational Exponents
6.1 nth Roots and Rational Exponents
Solving Equations by taking the “nth root” of both sides
Ex)
4
4
Ex)
5
5
W
h
e
n
t
h
e
e
x
p
o
n
e
n
t
i
s
E
V
E
N
y
o
u
m
u
s
t
u
s
e
t
h
e
P
l
u
s
/
M
i
n
u
s
W
h
e
n
t
h
e
e
x
p
o
n
e
n
t
i
s
O
D
D
y
o
u
d
o
n
’
t
u
s
e
t
h
e
P
l
u
s
/
M
i
n
u
s
Goal
Goal
3
3
6.1 nth Roots and Rational Exponents
6.1 nth Roots and Rational Exponents
Solving Equations
Ex)
4
4
Very Important
2 answers !
T
a
k
e
t
h
e
S
q
u
a
r
e
1
s
t
.
Example:
Solve the equation:
Note: index number
is even, therefore,
two answers.
S
O
L
U
T
I
O
N
M
u
l
t
i
p
l
y
e
a
c
h
s
i
d
e
b
y
2
.
t
a
k
e
5
t
h
r
o
o
t
o
f
e
a
c
h
s
i
d
e
.
S
i
m
p
l
i
f
y
.
(
x
– 2 )
3
= –14
S
O
L
U
T
I
O
N
U
s
e
a
c
a
l
c
u
l
a
t
o
r
.
(
x
+ 5 )
4
= 16
S
O
L
U
T
I
O
N
t
a
k
e
4
t
h
r
o
o
t
o
f
e
a
c
h
s
i
d
e
.
a
d
d
5
t
o
e
a
c
h
s
i
d
e
.
W
r
i
t
e
s
o
l
u
t
i
o
n
s
s
e
p
a
r
a
t
e
l
y
.
U
s
e
a
c
a
l
c
u
l
a
t
o
r
.
Ex. 4 Solving Equations Using nth Roots
A. 2x
4
= 162
B. (x – 2)
3
= 10
6.6 Solving Radical Equations
6.6 Solving Radical Equations
Goal
Goal
2
2
Solve equations that contain
Rational exponents
.
Ex. 6)
it
Ex: Simplify the Expression.
Assume all variables are positive.
a.
b.
(16g
4
h
2
)
1/2
= 16
1/2
g
4/2
h
2/2
= 4g
2
h
c.
d.
Explore the concepts of radicals and nth roots in solving equations involving exponents and radicals. Understand how to find the domain and range of functions graphically. Practice changing between radical and exponent notation, evaluating nth roots of real numbers, and solving real-life problems using nth roots. Dive into examples like determining the total mass of a spacecraft and finding the maximum speed of a ship based on power generated by a crew. Enhance your understanding of mathematical principles through practical applications.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Radicals and nth roots Solving equations with exponents and radicals
But first, some Domain and range review. Find the domain and range of the blue graph ?: < ? < R: 4 ? < Find the domain and range of the pink graph ?: < ? < R: y= 1.2
Finding Domain and Range State the domain and range of the function in the red SOLUTION ?: 2 ? < R: < ? 1
Find the domain and range of the graph Domain: x 0, Range: y 0 Domain and range: all real numbers
Objectives/Assignment Change between radical and exponent notation Evaluate nth roots of real numbers using both radical notation and rational exponent notation. Use nth roots to solve equations containing radicals and exponents other than 1 or 2.
Ex. 5: Using nth Roots in Real Life The total mass M (in kilograms) of a spacecraft that can be propelled by a magnetic sail is, in theory, given by:
2 . 0 015 fd m M = 4 3 where m is the mass (in kilograms) of the magnetic sail, f is the drag force (in newtons) of the spacecraft, and d is the distance (in astronomical units) to the sun. Find the total mass of a spacecraft that can be sent to Mars using m = 5,000 kg, f = 4.52 N, and d = 1.52 AU.
Solution The spacecraft can have a total mass of about 47,500 kilograms. (For comparison, the liftoff weight for a space shuttle is usually about 2,040,000 kilograms.
Ex. 6: Solving an Equation Using an nth Root NAUTICAL SCIENCE. The Olympias is a reconstruction of a trireme, a type of Greek galley ship used over 2,000 years ago. The power P (in kilowatts) needed to propel the Olympias at a desired speed, s (in knots) can be modeled by this equation: P = 0.0289s3 A volunteer crew of the Olympias was able to generate a maximum power of about 10.5 kilowatts. What was their greatest speed?
SOLUTION The greatest speed attained by the Olympias was approximately 7 knots (about 8 miles per hour).
Solve equations that contain square roots 1 1 Goal Solve the equation. Check for extraneous solutions. Key Step: Simple Radical = 3 x Ex.1) To raise each side of the equation to the same power. ( ) ( ) 3 2 2 = check your solutions!! x = 9 x 6.6 Solving Radical Equations
One Radical + = ( 2 46 ) 8 4 6 + + = 2 8 4 4 6 Ex.3) x + =( )2 = 100 92 4 10 10 = = = 100 4 6 2 + x 2 + x 2 + ( ) 8 8 2 = x 2 = x 8 8 2 10 4 6 x 8 2 Don t forget to check your solutions!! 46 6.6 Solving Radical Equations
Radicals with an Extraneous Solution x 3= Ex.5) = 4 x 9 3 ) 9 ( 4 ( ) ( 6 4 x )2 9 2 = = 3 + x 4x x x 4 = = x 2 x ( 4 9 ) 1 2 x x + 10 9 x x 0 = 1 3 ) 1 ( 4 )( 0 = = 9 1 x x Don t forget to check your solutions!! 6.6 Solving Radical Equations
Two Radicals Steps for two ) 2 ( 2 radical equations Set radical equal to radical Square both sides Solve for x = 12 2 2 0 + = 12 2 2 2 0 Ex.4) x x + 2 2 x =( = x x 2 x = 8 2 2 0 ) 12 12 ( ) 2 + x 2 x x 2 2 2 x 4 = 2 + 12 2 = 2 2 2 2 0 x x 12 = 6 2 6 x 6 x Don t forget to check your solutions!! = 6.6 Solving Radical Equations
Reflection on the Section Without solving, explain why + = 2 4 8 x has no solution. 6.6 Solving Radical Equations
Radical notation Radical Index Number 1n = a na n > 1 The index number becomes the denominator of the exponent. Radicand
More on Radicals na If n is odd a can be any number If n is even, then a must be a positive number or zero, otherwise there is no real solution.
Example: Radical form to Exponential Form Change to exponential form. 23 = 2 3x x ( or ) 2 13 = x or ( ) x 1 = 2 3
Example: Exponential to Radical Form Change to radical form. ( ) 23 2 x = 2 3 3 or x x The denominator of the exponent becomes the index number of the radical.
Using Rational Exponent Notation Rewrite the expression using RADICAL notation. ( )3 24 1 324 Ex) ( )4 28 1 428 Ex) 6.1 nth Roots and Rational Exponents
Ex. 2 Evaluating Expressions with Rational Exponents = = = 3 3 3 9 ( 9 ) 3 27 A. Using radical notation 2 Using rational exponent notation. 1 2 2 3 1 = = = 3 3 9 9 ( ) 3 27 1 OR 2 2 1 1 2 B. = = = = 32 5 2 2 4 32 5 ( 32 ) 5 1 1 1 2 = = = 32 OR 5 2 1 2 2 4 32 ( ) 5
Evaluate both ways (a) proficient 163/2 and (b) advanced323/5. SOLUTION Radical Form 163/2 ( )3 = Rational Exponent Form a. 163/2 (161/2)3 = b. 32 3/5 =1 64 1 = = 43 = 43 = 64 16 1 1 = = = 32-3/5 (321/5)3 323/5 5 32 323/5 ( )3 =1 1 8 = 23 1 8 =1 = 23
Cancelling radicals to solve equations x a. = 2 x x = 6 6 x b. y = 11 y 11 c. = 8 4 r r = r 4 4 4 4 4 4 4 r r d. = r r = 2 r
Equations with nth root radicals + = 3 6 6 12 x Key Step: Ex.2) 6 = = Before raising each side to the same power, you should isolate the radical expression on one side of the equation. 3x 3x 6 ( ) ( )3 6 3 = x 216 Don t forget to check it. 6.6 Solving Radical Equations
Solving Equations by taking the nth root of both sides 3 3 Goal 4 4 4= 81 x 5= Ex) 2 64 x Ex) 5 5 = 481 x 5= 32 x = 532 x = 3 x = 2 x When the exponent is EVEN you must use the Plus/Minus When the exponent is ODD you don t use the Plus/Minus 6.1 nth Roots and Rational Exponents
Solving Equations 4 4 ) 4 4= Take the Square 1st. ( 256 x Ex) = 4256 4 x Very Important 2 answers ! = 4 4 x x = 0 4 = 4 x x 4 = = 4 x 8 6.1 nth Roots and Rational Exponents
Example: Solve the equation: x = 7 7 x x 4 7 9993 9993 7 10000 + = + 4 x = = = 4 4 4 410000 10 Note: index number is even, therefore, two answers. x
1 2 x5 = 512 SOLUTION 1 2 x5= 512 x5= 1024 Multiply each side by 2. x = 5 1024 take 5th root of each side. x = 4 Simplify.
( x 2 )3 = 14 SOLUTION ( x 2 )3= 14 ( x 2 ) = 3 14 x = 3 14 + 2 x = 3 14 + 2 x = 0.41 Use a calculator.
( x + 5 )4 = 16 SOLUTION ( x + 5 )4 = 16 take 4th root of each side. ( x + 5 ) = + 4 16 add 5 to each side. x = + 4 16 5 x = 2 5 or Write solutions separately. x = 2 5 x = 3 x = 7 or Use a calculator.
Ex. 4 Solving Equations Using nth Roots A. 2x4 = 162 B. (x 2)3 = 10 2) (x = 10 = 3 = 4 2 162 x 3 x - = 2 10 + = 4 81 x 3 10 2 x = 4 81 x . 4 15 x = 3 x
Solve equations that contain Rational exponents. 2 2 Goal 3 2 = 3 2 ( 2 25 ) 250 = Ex. 6) 2 250 x 2 2 = = 125 ( 125 3x 2 ) ( ) 2 3 2 3 3x 2 3) 1 2 ( 2 25 ( 125 ( )2 5 25 ) 2 1) 2 15625 ( 2 = 1 3 x = x ( 2 125 ) = = 250 x it 6.6 Solving Radical Equations
Ex: Simplify the Expression. Assume all variables are positive. a. = 3 3z = 9 3 2 3 9 27z 327 z 2 1 18 rs 3 1 d. = 3 3 r s t 3 4 1 t 3 6 r 4 b. (16g4h2)1/2 = 161/2g4/2h2/2 = 4g2h 2 3 = 3 3 r s t 3 4 c. 5 5 5 x x = 5 10 y 10 y 5 x = 2 y
