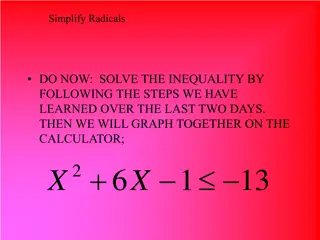Simplifying Algebraic Expressions with Dr. Frost
Master algebraic simplification with Dr. Frost's engaging exercises and explanations. Understand like terms, multiplying variables, and more through visual aids and activities. Learn the rules for combining terms and avoid common errors. Enhance your algebra skills and confidence in no time!
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Dr Frost Algebraic Simplification Objectives: Be able to simplify algebraic expressions involving addition, subtraction, multiplication and division.
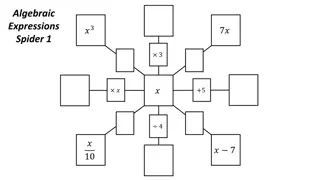
Starter Instructions: Given that each square is the sum of the two expressions below it, fill in the missing expressions. 10a + 2b 5a + b 5a + b ? 2a + b ? 3a 2a + b ? a a + b ? 2a b ? ?
What does these actually mean? In terms of what we re multiplying together. = 3 b 3b ? x2 = x x ? 9y2 = 9 y y ? 4xy3 = 4 x y y y ?
Activity Group things which you think are considered like terms. 4x2y 9x x2 3x3 2x2 y2 2x2y x -1 -x3 -3x2 5xy2 +4 5xy
Activity Answers: 9x x y2 -1 +4 5xy2 2x2y 4x2y 5xy 2x2 x2 -3x2 3x3 -x3 What therefore is the rule which determines if two terms are considered like terms ? They involve the same variables, and use the same powers. ?
Schoolboy ErrorsTM b3 + b2 = b5 b3 + b2 = 5b What is wrong with these?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 2x + x2 + 5x = x2 + 7x ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 2x + 3x2 + 8x 2x2 = x2 + 10x ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. x3 + x2 + x + x = x3 + x2 + 2x ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. x2y + xy2 - x = x2y + xy2 - x ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. y 3r = 3yr (or 3ry) ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 6x 3y = 18xy ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 6x + 3y = 6x + 3y ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 12qw q = 12q2w ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 3xy 3yz = 9xy2z ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 3x 3 = x ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 9?? 3? = 3x ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 8?2 4? = 2y ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 16??2 4? = 4xy ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 16?2?? 32?? ?? 2 ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 2x +9?2? 3?? 2 5? 2 ?
When adding algebraic terms, we can collect like terms together. + Don t mix up the first two! When multiplying algebraic terms, we just multiply each of the individual items. x When dividingalgebraic terms, we cancel out common items. 9??2 ? 8?2?2 2?2 x y ?2? ?