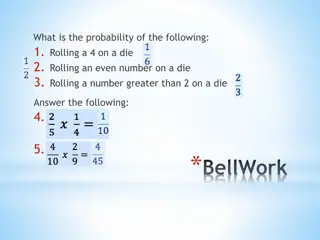Probability II Solutions: Revision Section A
This content provides solutions for probability questions in Chapter 19, focusing on soccer and rugby team wins, lollipop selection, and game winning probabilities. It includes calculations and explanations for various scenarios and tree diagrams.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
CHAPTER 19 Probability II Solutions: Revision - Section A
19 Revision and Exam Style Questions: Section A 3 5 1. The probability that Ben s soccer team wins this weekend is . The probability that his rugby league team wins this weekend is . 2 3 What is the probability that neither team wins this weekend? (i) P(Neither wins) = P(Soccer loses and Rugby loses) = P(Soccer loses) P(Rugby loses) 2 5 1 3 2 15 = =
19 Revision and Exam Style Questions: Section A 3 5 1. The probability that Ben s soccer team wins this weekend is . The probability that his rugby league team wins this weekend is . 2 3 What is the probability that only one of the teams wins? (ii) P(One team wins) = P(Soccer wins and Rugby loses) or P(Soccer loses and Rugby wins) = (P(Soccer wins) P(Rugby loses)) + (P(Soccer loses) P(Rugby wins)) 3 5 1 3 3 3 15+4 15 =7 15 +2 5 2 = =
19 Revision and Exam Style Questions: Section A 2. A packet of lollipops contains eight red lollipops and 14 blue lollipops. Two lollipops are selected at random without replacement. Draw a tree diagram to show the possible outcomes. (i) Write the probabilities on each branch. Tree diagram: 8 Red 14 Blue Total : 22 No replacement
19 Revision and Exam Style Questions: Section A 2. A packet of lollipops contains eight red lollipops and 14 blue lollipops. Two lollipops are selected at random without replacement. What is the probability that the two lollipops are of different colours? (ii) P(Two different) = P(1stRed and 2ndBlue) or P(1stBlue and 2ndRed) = (P(Red) P(Blue)) + (P(Blue) P(Red)) +14 8 22 14 22 8 = 21 21 8 33+8 = 33 =16 33
19 Revision and Exam Style Questions: Section A 2. A packet of lollipops contains eight red lollipops and 14 blue lollipops. Two lollipops are selected at random without replacement. What is the probability that the two lollipops are the same colour? (iii) P(Two same) = P(Red and Red) or P(Blue and Blue) = (P(Red) P(Red)) or (P(Blue) P(Blue)) +14 8 22 7 22 13 = 21 21 4 33 13 33 + = =17 33
19 Revision and Exam Style Questions: Section A 5 8 3. The probability of winning a game is . If the game is played three times, what is the probability of winning: 5 8 1-5 8=3 P(winning) = P(losing) = 8 three consecutive games? (i) 5 8 5 8 5 P(WWW) = ( and rule ) 8 125 512 =
19 Revision and Exam Style Questions: Section A 5 8 3. The probability of winning a game is . If the game is played three times, what is the probability of winning: at least two games? (ii) P(At least 2) = P(2 or 3 wins) = P(WWW) or P(WLW) or P(LWW) or P(WWL) + + 125 512 5 3 5 8 8 8 3 5 5 8 8 8 5 5 3 8 8 8 = + 350 512 = 175 512 =
19 Revision and Exam Style Questions: Section A 4. A bag contains five yellow marbles and seven green marbles. Two marbles are selected at random without replacement. What is the probability that at least one of the marbles selected is yellow? (i) P(At least 1 yellow) = P(YY) or P(YG) or P(GY) + + 12 4 5 12 7 5 12 5 7 = 11 11 11 5 33+35 132+35 = 132 =15 22
19 Revision and Exam Style Questions: Section A 4. A bag contains five yellow marbles and seven green marbles. Two marbles are selected at random without replacement. What is the probability that at least one of the marbles selected is yellow? (i) Alternatively P(At least 1 yellow) = 1 P(both green) 12 6 7 = 1- 11 = 1-7 22 15 22 =
19 Revision and Exam Style Questions: Section A 4. A bag contains five yellow marbles and seven green marbles. Two marbles are selected at random without replacement. If a marble is selected at random and replaced 72 times, how many times would you expect to get a yellow marble? (ii) 5 = P (Y) 12 5 = 72 times 72 12 = 30 yellow s expected
19 Revision and Exam Style Questions: Section A 5. Two boxes each contain green balls and yellow balls. Box A contains four green and three yellow balls. Box B contains four green and five yellow balls. Chris randomly chooses one ball from each box. Box A: 4 green 3 yellow Box B : 4 green 5 yellow Total: 7 Total : 9 What is the probability that both balls are green? (i) 4 7 4 P(GG) = ( and rule ) 9 16 23 =
19 Revision and Exam Style Questions: Section A 5. Two boxes each contain green balls and yellow balls. Box A contains four green and three yellow balls. Box B contains four green and five yellow balls. Chris randomly chooses one ball from each box. Box A: 4 green 3 yellow Box B : 4 green 5 yellow Total: 7 Total : 9 What is the probability that at least one of the balls is yellow? (ii) P(At least 1 yellow) = P(YY) or P(YG) or P(GY) +3 +4 3 7 5 7 4 7 5 = 9 9 9 4 21+5 21+20 = 63 47 63 =
19 Revision and Exam Style Questions: Section A 5. Two boxes each contain green balls and yellow balls. Box A contains four green and three yellow balls. Box B contains four green and five yellow balls. Chris randomly chooses one ball from each box. Box A: 4 green 3 yellow Box B : 4 green 5 yellow Total: 7 Total : 9 What is the probability that at least one of the balls is yellow? Alternatively (ii) P(At least 1 yellow) = 1 P(both green) = 1-4 7 4 9 = 1-16 23 47 63 =
19 Revision and Exam Style Questions: Section A 5. Two boxes each contain green balls and yellow balls. Box A contains four green and three yellow balls. Box B contains four green and five yellow balls. Chris randomly chooses one ball from each box. Box A: 4 green 3 yellow Box B : 4 green 5 yellow Total: 7 Total : 9 What is the probability that both balls are the same colour? (iii) +4 3 7 5 7 4 P(YY) or P(GG) = 9 9 =15 63+16 63 =31 63
19 Revision and Exam Style Questions: Section A 6. Jake has four blue t-shirts and three white t-shirts. On each of the three days, Friday, Saturday and Sunday, he selects one t-shirt at random to wear. Jake wears each t-shirt that he selects only once. What is the probability that Jake wears a blue t-shirt on Friday? (i) P(B) = 4 7
19 Revision and Exam Style Questions: Section A 6. Jake has four blue t-shirts and three white t-shirts. On each of the three days, Friday, Saturday and Sunday, he selects one t-shirt at random to wear. Jake wears each t-shirt that he selects only once. What is the probability that Jake wears a t-shirt of the same colour on all three days? Wears once = No replacement. P(Same colour) = P(BBB) or P(WWW) = [P(B) P(B) P(B)] + [P(W) P(W) P(W)] =4 35 =5 35 (ii) +3 =4 7 3 35+1 6 2 7 2 6 1 5 5 =1 7
19 Revision and Exam Style Questions: Section A 6. Jake has four blue t-shirts and three white t-shirts. On each of the three days, Friday, Saturday and Sunday, he selects one t-shirt at random to wear. Jake wears each t-shirt that he selects only once. What is the probability that Jake does not wear a t-shirt of the same colour on consecutive days? (iii) P(No same colour on consecutive days) = P(BWB) or P(WBW) = [P(B) P(W) P(B)] + [P(W) P(B) P(W)] +3 =10 35 =4 =6 7 3 6 3 7 4 6 2 5 5 35+4 =2 35 7
19 Revision and Exam Style Questions: Section A 7. There are 12 chocolates in a box. Four of the chocolates have caramel centres, four have orange centres and four have strawberry centres. Abdul randomly selects two chocolates and eats them. What is the probability that the two chocolates have orange centres? (i) P(OO) = 4 12 3 11 = 1 11
19 Revision and Exam Style Questions: Section A 7. There are 12 chocolates in a box. Four of the chocolates have caramel centres, four have orange centres and four have strawberry centres. Abdul randomly selects two chocolates and eats them. What is the probability that the two chocolates have the same centre? (ii) P(2 same) = P(OO) or P(CC) or P(SS) + 12 3 1 11+1 3 11 4 12 3 4 12 3 4 = 11 11+1 11 11 = 11 =
19 Revision and Exam Style Questions: Section A 7. There are 12 chocolates in a box. Four of the chocolates have caramel centres, four have orange centres and four have strawberry centres. Abdul randomly selects two chocolates and eats them. What is the probability that the two chocolates have different centres? (iii) P(2 different centres) = P(OC) or P(OS) or P(CO) or P(CS) or P(SO) or P(SC) 11 + + + + + 12 4 4 12 4 4 12 4 4 12 4 4 12 4 4 12 4 4 = 11 11 11 11 11 4 33 6 8 11 = =
19 Revision and Exam Style Questions: Section A 7. There are 12 chocolates in a box. Four of the chocolates have caramel centres, four have orange centres and four have strawberry centres. Abdul randomly selects two chocolates and eats them. What is the probability that the two chocolates have different centres? (iii) Alternatively P(2 different centres) = 1 P(same centres) =1-3 11 =8 11
19 Revision and Exam Style Questions: Section A 8. Sarah often oversleeps and arrives late for school. She has estimated the probability that she will oversleep on Monday as 25% and on Tuesday as 35%. The tree diagram shows these probabilities.
19 Revision and Exam Style Questions: Section A 8. Sarah often oversleeps and arrives late for school. She has estimated the probability that she will oversleep on Monday as 25% and on Tuesday as 35%. The tree diagram shows these probabilities. Copy the tree diagram and fill in the probabilities that Sarah does not oversleep. (i) Monday 1 0.25 = 0 75 Tuesday 1 0 35 = 0 65
19 Revision and Exam Style Questions: Section A 8. Sarah often oversleeps and arrives late for school. She has estimated the probability that she will oversleep on Monday as 25% and on Tuesday as 35%. The tree diagram shows these probabilities. Calculate the probability that Sarah oversleeps on both Mondays and Tuesdays. (ii) P(Oversleeps both) = P(Oversleeps) P(Oversleeps) = 0 25 0 35 = 0 0875
19 Revision and Exam Style Questions: Section A 8. Sarah often oversleeps and arrives late for school. She has estimated the probability that she will oversleep on Monday as 25% and on Tuesday as 35%. The tree diagram shows these probabilities. Calculate the probability that Sarah oversleeps on exactly one of the two days. (iii) P(Oversleeps on one day) = P(OD) or P(DO) = (0 25 0 65) + (0 75 0 35) = 0 1625 + 0 2625 = 0 425
19 Revision and Exam Style Questions: Section A 9. A card is taken from a standard deck. This card is replaced and a second card is drawn. What is the probability that the cards drawn are: a seven and a queen? (i) 52 4 4 P(7 and Queen) = ( and rule ) 52 1 = 169
19 Revision and Exam Style Questions: Section A 9. A card is taken from a standard deck. This card is replaced and a second card is drawn. What is the probability that the cards drawn are: two red tens? (ii) 52 2 2 P(Red 10 and Red 10) = ( and rule ) 52 1 = 676
19 Revision and Exam Style Questions: Section A 9. A card is taken from a standard deck. This card is replaced and a second card is drawn. What is the probability that the cards drawn are: a spade or an ace? (iii) Not mutually exclusive P(A spade or on Ace) = P(spade) + P(Ace) P(Ace + spade) =13 52+4 52-1 52 =17 52-1 =16 52 52 =4 13
19 Revision and Exam Style Questions: Section A 9. A card is taken from a standard deck. This card is replaced and a second card is drawn. What is the probability that the cards drawn are: not picture cards? (iv) 40 52 40 P(Not picture) = 52 100 169 =
19 Revision and Exam Style Questions: Section A 10.If you draw three cards from a deck without replacement, what is the probability that: all three cards are red? (i) 26 52 25 51 24 P(RRR) = 50 2 = 17
19 Revision and Exam Style Questions: Section A 10.If you draw three cards from a deck without replacement, what is the probability that: you don t draw any spades? (ii) P(No spades) = 13 spades ==> 52 13 = 39 not spades 39 52 38 51 37 = 50 703 1,700 =
19 Revision and Exam Style Questions: Section A 10.If you draw three cards from a deck without replacement, what is the probability that: you draw a club, a heart and a diamond (in that order)? (iii) 13 52 13 51 13 P( ) = 50 169 10,200 =
19 Revision and Exam Style Questions: Section A 10.If you draw three cards from a deck without replacement, what is the probability that: you draw a club, a heart and a diamond in any order? (iv) (CHD, CDH, DCH, DHC, HCD, HDC) 6 13 52 13 51 13 50 169 10200 6 169 1700 = =
19 Revision and Exam Style Questions: Section A 11.A survey of 154 people was carried out. Participants were asked whether they liked tea or coffee. Some of the results are recorded in the Venn diagram below. Of those surveyed, 21 people did not like either tea or coffee. Complete the diagram. (i) 21 liked neither 154 people 154 (52 + 36 + 21) = coffee only = 45 Tea Coffee 52 45 36 21
19 Revision and Exam Style Questions: Section A 11.A survey of 154 people was carried out. Participants were asked whether they liked tea or coffee. Some of the results are recorded in the Venn diagram below. A person is chosen at random from those surveyed. What is the probability that the person liked both coffee and tea? (ii) 52 154 P(Both Tea and coffee) = 26 77 = Tea Coffee 52 45 36 21
19 Revision and Exam Style Questions: Section A 11.A survey of 154 people was carried out. Participants were asked whether they liked tea or coffee. Some of the results are recorded in the Venn diagram below. What percentage of the people surveyed liked one beverage only? Give your answer correct to one decimal place. (iii) P(One beverage only) = P(Tea or Coffee) = P(Tea only) + P(Coffee only) 36 154+45 154 81 154 = 0 5259 100 = Tea Coffee = 52 45 36 = 52 59 21 = 52 6%(to one decimal place)
