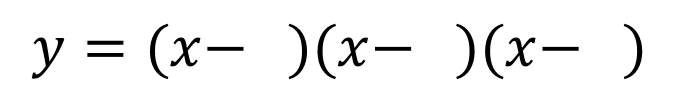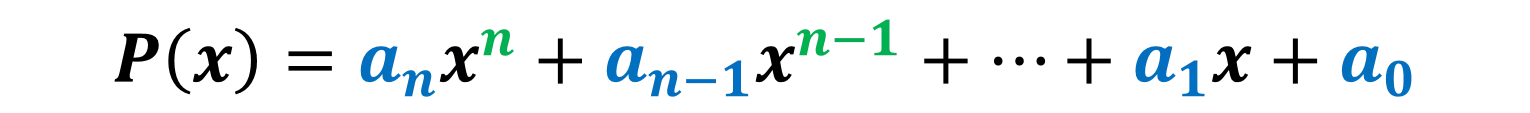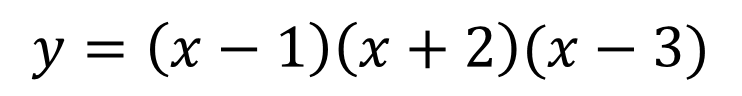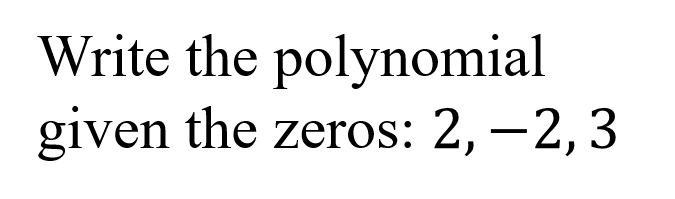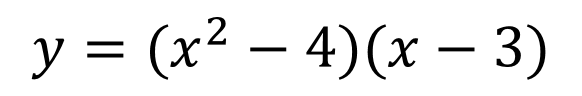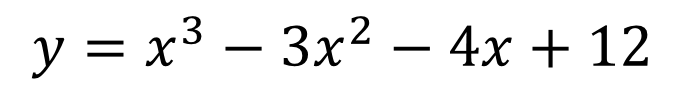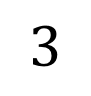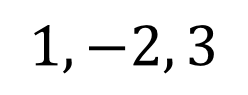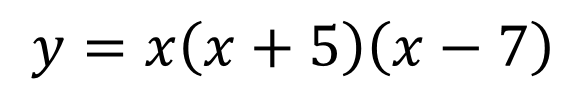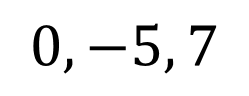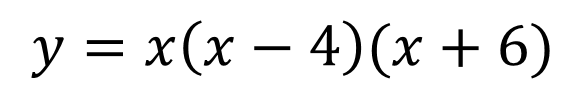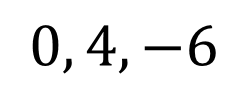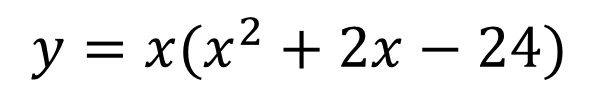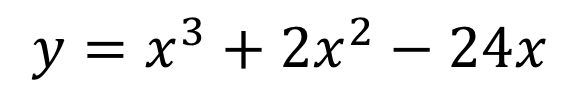Polynomials: Zeros, Factors, and Graphs

Understanding polynomials, linear factors, and zeros. Learn how to write and graph polynomial functions, find roots and x-intercepts, apply the Factor Theorem, and plot graphs using zeros and end behaviors.

• Polynomials
• Zeros
• Factors
• Graphs
• Factor Theorem

clement Follow

Uploaded on Aug 17, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. 5-2 Polynomials, Linear Factors, & Zeros Today s Objective: I can write and graph a polynomial function

2. Roots, Zeros & x-intercepts ? ? = ????+ ?? ??? ?+ + ??? + ?? Factor Theorem ? ? is a linear factor of the polynomial ?(?) if and only if b is a zero of the polynomial function ?(?) Find the zeros ? = ?3+ 2?2 24? Write the polynomial given the zeros: 2, 2,3 ? = ? 1 ? + 2 (? 3) ? = (? )(? )(? ) 2 +2 3 ? = ?(?2+ 2? 24) 1, 2,3 ? = (?2 4)(? 3) ? = ?3 3?2 4? + 12 ? = ? ? 4 (? + 6) ? = ? ? + 5 ? 7 0, 5,7 0,4, 6

3. Graphing with zeros ?(?) = ?(? 4)(? + 3) 1. Find and plot the zeros 2. Sketch end behavior 3. Pick easy midpoints between zeros to estimate turning point Zeros: 0,4, 3 ?( 2) = 2( 2 4)( 2 + 3) = 12 ?(2) =2(2 4)(2 + 3) = 20

4. Zeros with Multiplicity ?(?) = (? + 2)2(? 2)(? 3) 1. Find and plot the zeros 2. Sketch end behavior 3. Pick easy midpoints between zeros to estimate turning point ?(?) = (? + 2)(? + 2)(? 2)(? 3) Even multiplicity turns graph at zero Odd multiplicity pauses graph zero Zeros: 2, 2,2,3 (0 + 2)2(0 2)(0 3) ?(0) = = 24 2.5 + 22(2.5 2)(2.5 3) ?(2.5) = p. 293:9-33 mult. of 3 = 5