Orbital Mechanics and Satellites Overview
This content provides calculations for the orbital speed and period of the International Space Station, as well as the orbital radius of an Earth satellite with a 24-hour period. It explains the concept of artificial satellites, different types of orbits such as Low Earth Orbit (LEO), Medium Earth Orbit (MEO), and Geostationary Orbit (GEO), and their altitudes above Earth's surface. The discussion also includes the time periods of satellites in various orbits and the concept of escape velocity.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
SciDoc Orbits & escape velocity Orbits & escape velocity 27/09/2024 27/09/2024 Q1. Calculate (a) the orbital speed and (b) period of the International Space Station. Earth radius, R = 6400 km Orbital height of the ISS, H = 300 km Earth mass, M = 6.0 x 10 24 kg G = 6.672 x 10 -11 N m 2 kg 2 Q2. Calculate the orbital radius of an Earth satellite having an orbital period of 24 hours.
SciDoc Q1 review Q1 review (a) Orbital speed v = (GM / r) BUT: r = R + H= (6400 + 300)km = 6700 km = 6.7 x 106 m and so: v= (6.672 x 10 -11 x 6.0 x 10 24 / 6.7 x 106) = (4.003 x 10 14 / 6.7 x 106) = (5.975 x 10 7) orbital speed = 7.73 x 103 ms-1 = 7.73 kms-1 (b) Orbital period T = (4 2 r 3 / GM) = (4 2 x (6.7 x 106)3 ) / (6.672 x 10 -11 x 6.0 x 10 24) = (1.187 x 10 22 / 4.003 x 10 14) = (2.966 x 10 7) orbital period = 5.45 x 103 s = 90.8 minutes = 1h 30 mins
SciDoc Q2 review Q2 review Earth mass, M = 6.0 x 10 24 kg; G = 6.672 x 10 -11 N m 2 kg - 2 T = (4 2 r 3 / GM) rearranged becomes: r 3 = T 2 GM / 4 2 r 3 = (24 x 60 x 60)2 x (6.672 x 10 -11 x 6.0 x 10 24 ) / 4 2 r 3 = (86400)2 x (4.003 x 10 14) / 4 2 r 3 = (7.465 x 10 9 ) x (4.003 x 10 14) / 4 2 r 3 = 7.570 x 10 22 r = 4.23 x 10 7 m = 42 300 km This is 35 900 km above the Earth s surface
SciDoc What is an artificial satellite? What is an artificial satellite? An artificial satellite is an object that people have made and launched into orbit using rockets. Satellites vary in size. The largest artificial satellite is the International Space Station (ISS). The main part of this is as big as a large five-bedroom house, but including solar panels, it is as large as a rugby field.
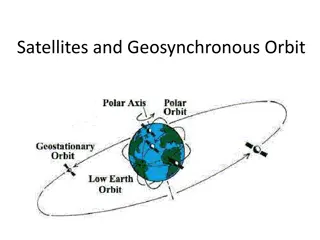
SciDoc Types of orbit Types of orbit Altitudes of satellites above the Earth s surface: Low Earth orbit (LEO) from 200 to 2000 km, for example, the ISS orbits at 400 km with a speed of 28 000 km/h, and time for one orbit is about 90 minutes. Medium Earth orbit (MEO) most MEO satellites are at an altitude of 20 000 km, and time for one orbit is 12 hours. Geostationary orbit (GEO) 36 000 km above the Earth. Time for one orbit is 24 hours. This is to match the rotation of the Earth so that the satellite appears to stay above the same point above the Earth s surface. This is used for many communications and weather satellites.
SciDoc T/N: Types of orbit T/N: Types of orbit Calculate the time period of these satellites above the surface of Earth (remember radius of Earth is 6400 km!) LEO: 200-2000 km. ISS space station, telecommunications. a) LEO 200 km above Earth s surface b) MEO 20,000 km above Earth s surface c) GEO 36,000 km above Earth s surface. MEO: 20,000 km. Used for GPS. GEO: Communications/TV. Over equator. What happens to the period as the radius of orbit increase? Why?
SciDoc Escape velocity Escape velocity The escape velocity from a planet is the minimum velocity an object must be given to escape from the planet when projected vertically from the surface. The gravitational potential V at a distance r from the centre of the planet of mass M is given by ? = ?? ? To move an object of mass m from the surface to infinity, the work that must be done is ? = ? ? =??? ? Stretch: How can we use this expression to obtain the velocity needed to escape the Earth s gravitational field (i.e. the escape velocity)?
SciDoc Escape velocity Escape velocity For the object to escape, the kinetic energy must be more than the work required: 1 Therefore1 ? 2??2 ? Stretch: What is the escape velocity for Earth? (Earth s radius = 6400 km) 2??2 ??? 2?? ? Escape velocity is then given by ?esc= And by using ? =?? the escape velocity which is: ?, we obtain a final expression for ?esc= 2??
SciDoc Energy of orbiting satellite Energy of orbiting satellite Consider a satellite of mass m in a circular orbit of radius r, about a spherical planet or star of mass M. The speed of the satellite v is given by: ?2=?? ? as derived last lesson. What is the kinetic energy Ek of the satellite? 1 2??2=1 2? ?? ?=??? 2?
SciDoc Energy of orbiting satellite Energy of orbiting satellite The satellite is at distance r from the centre of the planet. At this distance The gravitational potential ? = ?? ?. Stretch: Sketch a graph of kinetic, potential & total energy of a potential against the radius of orbit. The satellite s GPE: ??= ?? = ??? ? Therefore the total energy of the satellite ?tot= ??+ ??: ?tot= ??? +??? = ??? ? 2? 2?
SciDoc Energy of orbiting satellite Energy of orbiting satellite Therefore, for a satellite in a circular orbit of radius r, its total energy is equal to: ?tot= ??? 2?
SciDoc Area under graphs Area under graphs The graph shows how the force of gravity on a 1kg mass varies with distance from infinity to the surface of a planet. What does the area under the curve represent? The area under the curve represents the work done to move the 1kg mass from the surface to infinity. Work done = Force Distance
SciDoc Area under graphs Area under graphs What does the area under this graph represent? (look at your equation sheet if it helps). Vfrom area under graph of g against r.
SciDoc Gravitational fields recap Gravitational fields recap ?3 ?2=?? ? =? ?= ? ?=?? Gravitational field strength Satellite motions ?2 4 2 ? ? ? = ??? Potential gradient Energy of satellite = 2? ? =? ?=? ? Gravitational potential Escape velocity 2?? ? ???? = = 2?? ? F=??2 ? =??? ?2= ? ? Newton s law of gravity Centripetal force = ? 2? ? ?
SciDoc Questions Questions Q1. By using equations for potential and kinetic energy, derive the equation for escape velocity GM 2 = v R Q2. Calculate the escape velocity for the following planets: a) Mars: mass = 6.46 1023 kg, radius = 3.39 106 m b) Mercury: mass = 3.35 1023 kg, radius = 2.44 106 m c) Venus: mass = 4.90 1023 kg, radius = 6.06 106 m
SciDoc Answers Answers
SciDoc Exam question Exam question Complete the exam questions.



![[PDF⚡READ❤ONLINE] Neptune: The Planet, Rings, and Satellites](/thumb/21522/pdf-read-online-neptune-the-planet-rings-and-satellites.jpg)