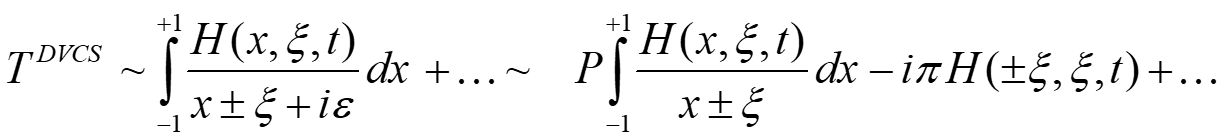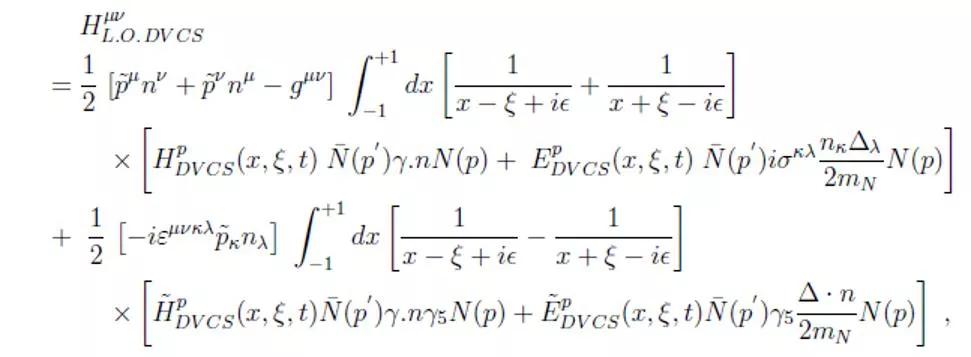Nucleon Tomography and Proton Charge Radius Exploration
Nucleon tomography
GDR QCD, 29/09/2016
Michel Guidal (IPN Orsay)
(from data to GPDs and proton charge radius)
JLab
JLab
Hall A
Hall A
JLab
JLab
CLAS
CLAS
HERMES
HERMES
DVCS
DVCS
BSA
BSA
DVCS
DVCS
lTSA
lTSA
DVCS
DVCS
BSA,lTSA,tTSA,BCA
BSA,lTSA,tTSA,BCA
DVCS unpol. and
DVCS unpol. and
B-pol. X-sections
B-pol. X-sections
DVCS
DVCS
unpol. X-section
unpol. X-section
DVCS
DVCS
B-pol. X-section
B-pol. X-section
H
q
(
x
,
,
t
)
but only
and
t
experimentally accessible
In general,
8
GPD quantities accessible
(sub-)Compton Form Factors
with
Given the well-established
LT-LO
DVCS+BH amplitude
DVCS
Bethe-Heitler
G
P
D
s
Can one recover the
8
CFFs
from the DVCS observables?
Two (quasi-) model-independent approaches
to extract, at fixed
x
B
,
t
and
Q
2
(« local » fitting)
,
the CFFs from the DVCS observables
UL
~
sin
Im{F1
H
+
(F
1
+F
2
)(
H
+ x
B
/2
E
) –
kF
2
E
+…
}d
~
~
LU
~
sin
Im{F1
H
+
(F
1
+F
2
)
H
-kF
2
E
}d
~
1/ Mapping and linearization
If enough observables measured, one has a system
of 8 equations with 8 unknowns
Given reasonable approximations
(leading-twist dominance,
neglect of some 1/Q
2
terms,...)
, the system can be linear
(practical for the error propagation)
K
.
K
u
m
e
r
i
c
k
i
,
D
.
M
u
e
l
l
e
r
,
M
.
M
u
r
r
a
y
P
h
y
s
.
P
a
r
t
.
N
u
c
l
.
4
5
(
2
0
1
4
)
4
,
7
2
3
2/ «Brute force » fitting
2
minimization (with
MINUIT + MINOS
) of the
available DVCS observables at a given
x
B
,
t
and
Q
2
point
by varying the CFFs within a limited hyper-space
(e.g. 5xVGG)
However, as some observables are largely dominated by
a single or a few CFFs, there is a convergence (i.e. a well-defined
minimum
2
) for these latter CFFs.
The contribution of the non-converging CFF enters in
the error bar of the converging ones. For instance (naive):
Examples of correlation between
H
Im
and
H
Im
~
2/ «Brute force » fitting
2
minimization (with
MINUIT + MINOS
) of the
available DVCS observables at a given
x
B
,
t
and
Q
2
point
by varying the CFFs within a limited hyper-space
(e.g. 5xVGG)
However, as some observables are largely dominated by
a single or a few CFFs, there is a convergence (i.e. a well-defined
minimum
2
) for these latter CFFs.
The contribution of the non-converging CFF enters in
the error bar of the converging ones.
unpol.sec.eff.
+
beam pol.sec.eff.
2
minimization
unpol.sec.eff.
+
beam pol.sec.eff.
2
minimization
beam spin asym.
+
long. pol. tar. asym
unpol.sec.eff.
+
beam pol.sec.eff.
2
minimization
beam spin asym.
+
long. pol. tar. asym
beam charge asym.
+
beam spin asym
+
…
linearization
R
e
p
t
.
P
r
o
g
.
P
h
y
s
.
7
6
(
2
0
1
3
)
0
6
6
2
0
2
M
.
G
.
,
H
.
M
o
u
t
a
r
d
e
,
M
.
V
a
n
d
e
r
h
a
e
g
h
e
n
C
L
A
S
c
o
l
l
.
P
R
L
1
1
5
(
2
0
1
5
)
,
2
1
2
0
0
3
H
a
l
l
A
c
o
l
l
.
P
R
C
9
2
(
2
0
1
5
)
,
0
5
5
2
0
2
C
L
A
S
c
o
l
l
.
P
R
L
1
1
4
(
2
0
1
5
)
,
0
3
2
0
0
1
C
L
A
S
c
o
l
l
.
P
R
D
9
1
(
2
0
1
5
)
,
0
5
2
0
1
4
N
e
w
r
e
c
e
n
t
d
a
t
a
f
r
o
m
J
L
a
b
:
(
u
n
p
o
l
.
a
n
d
b
e
a
m
-
p
o
l
.
x
-
s
e
c
t
i
o
n
s
)
(
l
T
S
A
)
(
l
T
S
A
)
(
u
n
p
o
l
.
a
n
d
b
e
a
m
-
p
o
l
.
x
-
s
e
c
t
i
o
n
s
)
C
L
A
S
c
o
l
l
.
P
R
L
1
1
5
(
2
0
1
5
)
,
2
1
2
0
0
3
R
.
D
u
p
r
é
,
M
.
G
.
,
M
.
V
a
n
d
e
r
h
a
e
g
h
e
n
a
r
X
i
v
:
1
6
0
6
.
0
7
8
2
1
[
h
e
p
-
p
h
]
CLAS
&
CLAS
,
lTSA & DSA
Hall A
&
R
.
D
u
p
r
é
,
M
.
G
.
,
M
.
V
a
n
d
e
r
h
a
e
g
h
e
n
a
r
X
i
v
:
1
6
0
6
.
0
7
8
2
1
[
h
e
p
-
p
h
]
CLAS
&
CLAS
,
lTSA & DSA
Hall A
&
I
f
(
M
.
B
u
r
k
h
a
r
d
t
)
H
o
w
e
v
e
r
,
t
h
i
s
f
o
r
m
u
l
a
i
n
v
o
l
v
e
s
:
W
h
i
l
e
w
e
e
x
t
r
a
c
t
:
N
e
e
d
t
o
e
s
t
i
m
a
t
e
:
(
a
s
s
u
m
i
n
g
)
f
o
r
«
I
n
t
e
g
r
a
t
e
d
»
r
a
d
i
u
s
f
r
o
m
e
l
a
s
t
i
c
f
o
r
m
f
a
c
t
o
r
F
1
u
s
i
n
g
:
r
e
c
e
n
t
C
O
M
P
A
S
S
m
e
a
s
u
r
e
m
e
n
t
(
I
W
H
S
S
2
0
1
6
)
The
axial
charge
(H
im
)
appears to be more « concentrated » than
the
electromagnetic
charge
(H
im
)
~
C
o
n
f
i
r
m
e
d
b
y
n
e
w
C
L
A
S
A
_
U
L
a
n
d
A
_
L
L
d
a
t
a
:
P
h
y
s
.
R
e
v
.
D
9
1
(
2
0
1
5
)
5
,
0
5
2
0
1
4
The Bethe-Heitler process
M
.
B
o
e
r
,
M
G
J
.
P
h
y
s
.
G
4
2
(
2
0
1
5
)
3
,
0
3
4
0
2
3
M
.
B
o
e
r
,
M
G
J
.
P
h
y
s
.
G
4
2
(
2
0
1
5
)
3
,
0
3
4
0
2
3
M
.
B
o
e
r
,
M
G
J
.
P
h
y
s
.
G
4
2
(
2
0
1
5
)
3
,
0
3
4
0
2
3
M
.
B
o
e
r
,
M
G
J
.
P
h
y
s
.
G
4
2
(
2
0
1
5
)
3
,
0
3
4
0
2
3
"Exploring the concept of nucleon tomography to understand proton charge radius and Generalized Parton Distributions (GPDs) in theoretical and experimental physics. Discussions on extracting Compton Form Factors (CFFs) from Deeply Virtual Compton Scattering (DVCS) observables using advanced methodologies. Insights into mapping, linearization, and brute force fitting techniques. Examples of correlation analysis between specific parameters. A comprehensive study on recovering GPD quantities from DVCS measurements."
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
GDR QCD, 29/09/2016 Nucleon tomography (from data to GPDs and proton charge radius) Michel Guidal (IPN Orsay)
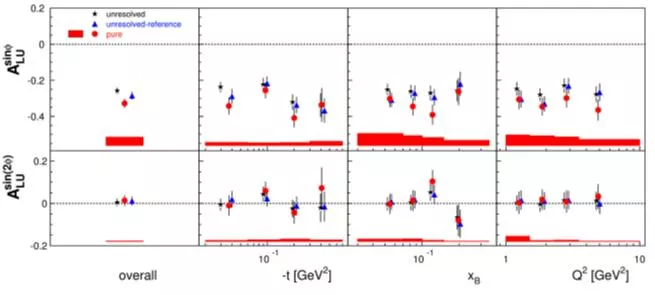
JLab Hall A DVCS DVCS B-pol. X-section unpol. X-section JLab CLAS DVCS BSA DVCS lTSA DVCS unpol. and B-pol. X-sections HERMES DVCS BSA,lTSA,tTSA,BCA
+ + 1 1 ( , , ) ( x , , ) H x t H x t + + TDVCS ~ ~ ( , , ) dx P dx i H t + x i 1 1 Hq(x, ,t) but only and t experimentally accessible
In general, 8 GPD quantities accessible (sub-)Compton Form Factors with
Given the well-established LT-LO DVCS+BH amplitude DVCS Bethe-Heitler GPDs Can one recover the 8 CFFs from the DVCS observables? Obs= Amp(DVCS+BH) CFFs Two (quasi-) model-independent approaches to extract, at fixed xB, t and Q2( local fitting), the CFFs from the DVCS observables
1/ Mapping and linearization If enough observables measured, one has a system of 8 equations with 8 unknowns Given reasonable approximations (leading-twist dominance, neglect of some 1/Q2terms,...), the system can be linear (practical for the error propagation) ~ LU ~ sin Im{F1H + (F1+F2)H -kF2E}d UL ~ sin Im{F1H+ (F1+F2)(H + xB/2E) kF2E+ }d ~ ~ K. Kumericki, D. Mueller, M. Murray Phys.Part.Nucl. 45 (2014) 4, 723
2/ Brute force fitting 2minimization (with MINUIT + MINOS) of the available DVCS observables at a given xB, t and Q2point by varying the CFFs within a limited hyper-space (e.g. 5xVGG) The problem can be (largely) underconstrained: JLab Hall A: pol. and unpol. X-sections JLab CLAS: BSA + TSA 2 constraints and 8 parameters ! However, as some observables are largely dominated by a single or a few CFFs, there is a convergence (i.e. a well-defined minimum 2) for these latter CFFs. The contribution of the non-converging CFF enters in the error bar of the converging ones. For instance (naive): If -10<x<10:
~ Examples of correlation between HImand HIm Polarized beam, unpolarized target (BSA) : ~ LU ~ sin Im{F1H + (F1+F2)H -kF2E}d
2/ Brute force fitting 2minimization (with MINUIT + MINOS) of the available DVCS observables at a given xB, t and Q2point by varying the CFFs within a limited hyper-space (e.g. 5xVGG) The problem can be (largely) underconstrained: JLab Hall A: pol. and unpol. X-sections JLab CLAS: BSA + TSA 2 constraints and 8 parameters ! However, as some observables are largely dominated by a single or a few CFFs, there is a convergence (i.e. a well-defined minimum 2) for these latter CFFs. The contribution of the non-converging CFF enters in the error bar of the converging ones. M.G. EPJA 37 (2008) 319 M.G. PLB 689 (2010) 156 M.G. PLB 693 (2010) 17 M.G. & H. Moutarde EPJA 42 (2009) 71 M.G. & M. Boer J.Phys.G 42 (2015) 034023
unpol.sec.eff. + beam pol.sec.eff. 2minimization
unpol.sec.eff. beam spin asym. + + beam pol.sec.eff. long. pol. tar. asym 2minimization
unpol.sec.eff. beam spin asym. beam charge asym. + + + beam pol.sec.eff. long. pol. tar. asym beam spin asym + 2minimization linearization
M.G., H. Moutarde, M. Vanderhaeghen Rept.Prog.Phys. 76 (2013) 066202
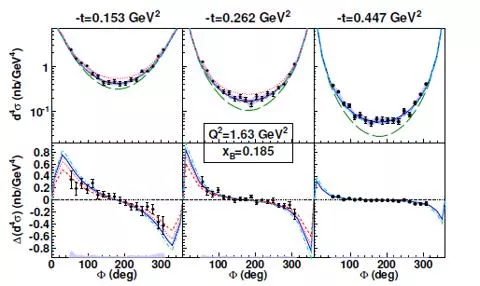
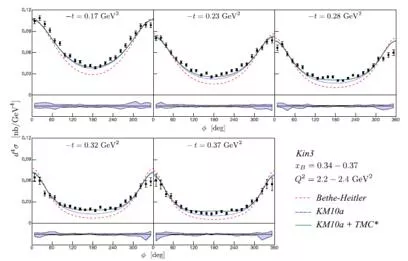
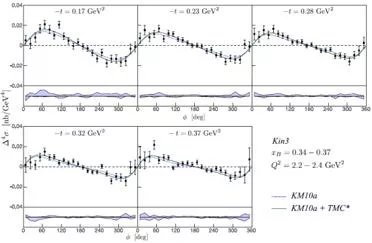
New recent data from JLab: CLAS coll. PRL 115 (2015), 212003 (unpol. and beam-pol. x-sections) Hall A coll. CLAS coll. CLAS coll. PRC92 (2015), 055202 (unpol. and beam-pol. x-sections) PRL 114 (2015), 032001 PRD91 (2015), 052014 (lTSA) (lTSA)
R. Dupr, M.G., M. Vanderhaeghen arXiv:1606.07821 [hep-ph] CLAS & CLAS , lTSA & DSA Hall A &
R. Dupr, M.G., M. Vanderhaeghen arXiv:1606.07821 [hep-ph] CLAS & CLAS , lTSA & DSA Hall A &
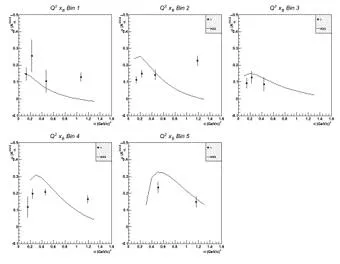
(M. Burkhardt) If However, this formula involves: While we extract: Need to estimate: (assuming )
The axial charge (Him) appears to be more concentrated than the electromagnetic charge (Him) ~
Confirmed by new CLAS A_UL and A_LL data: Phys.Rev. D91 (2015) 5, 052014
We have developped a fitting method to extract CFFs from data in which the influence of the subdominant CFFs end up in the uncertainties of the dominant CFFs First new insights on nucleon structure already emerging from current data: in particular, the rise of the proton radius (and density) as x decreases
