Multivariate Adaptive Regression Splines (MARS)
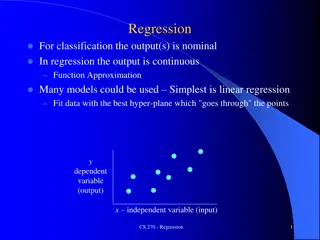
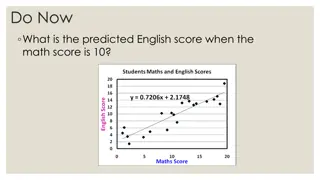
Multivariate Adaptive Regression Splines (MARS) is a flexible modeling technique that constructs complex relationships using a set of basis functions chosen from a library. The basis functions are selected through a combination of forward selection and backward elimination processes to build a smooth and accurate model without overfitting. By leveraging different types of terms such as constant terms, hockey stick functions, and interactions between predictors, MARS offers a powerful approach to regression analysis. The comparison with Classification And Regression Trees (CART) highlights the unique features of MARS models.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Multivariate Adaptive Regression Splines (MARS)
Library of basis functions/terms 1-dimensional linear spline (t represents the knot): Basis collection C: |C| < 2 x n x p
MARS In a multi-dimensional spline the number potential basis functions (i.e. terms) grow exponentially curse of dimensionality ? ? = ??+ ?? ?(?) ?=1 A partial remedy is a greedy forward search algorithm Create a simple basis-construction dictionary Construct basis functions on-the-fly Choose the best-fit basis function at each step Don t drop terms once added
MARS The terms in the MARS model are chosen from the library of basis hockey stick functions. ? ? = ??+ ?? ?(?) ?=1 After forward selection is finished, then backward elimination will be employed at which point terms may be dropped, particularly if some internal cross-validation is performed.
Again the library/catalog consists of 1-dim linear spline (t represents the knot): Basis collection C: |C| < 2 x n x p
MARS vs. CART MARS models are similar to simple CART models, but the terms are not made up of indicator functions that specify the path to the terminal nodes, thus the resulting fit is smoother. CART (discussed soon) MARS CART = Classification And Regression Trees
The MARS procedure (1st stage) 1. 2. 3. Initialize basis set M with a constant function Form candidates (cross-product of M with set C) Add the best-fit basis pair (decrease residual error the most) into M M (old) C M (new)
Types of Terms (?(?)) Constant term (??) Hockey stick function based on a single numeric predictor (??), e.g. ??? = ?? ??+ or ?? ??+ A product of two hockey stick functions based on two different predictors (?? ??? ??), e.g. ??,?? = ?? ??+?? ?? + A term equal to a single predictor or the product (i.e. interaction) of two predictors, e.g. ?? ?? ?? ?? Terms using dummy variables arising from any predictors that are factors, e.g. ???,??? ???, ?? ?? ??+ ???
The MARS procedure (1st stage) 4. Repeat from step 2 (until e.g., |M| > max terms chosen) Stop when one of the conditions is met: Adding a term changes R2 by less than 0.001. Reached an R2 of .999 or more. GCV criteria fails to improve Reach numerical accuracy limits
The MARS procedure (2nd stage) The final model typically over fits the data need to reduce the model size (# of terms) Backward deletion procedure 1. Remove term which causes the smallest increase in residual error 2. Compute GCV 3. Repeat step 1 Choose the model size with minimum GCV.
Generalized Cross Validation (GCV) GCV is not true cross-validation, however it is computationally much less expensive! The numerator is simply the RSS and the denominator inflates RSS based on ?(?) the effective number of parameters in the model and the number of knots used. Different versions of the denominator exist. ? ?? ? ?? ? ?=1 ? 2 = ?=1 ? 1 ? ? ?? ?? ??? ? = 2 2 ? 1 ?(?) ? ?
Discussion Hierarchical model (reduces search computation) High-order term exists some lower-order footprints exist Restriction - Each input appears at most once in a product/interaction term. e.g.(Xj - t1) * (Xj t2) is not considered Set upper limit on order of interaction Upper limit of degree = 1 additive model Upper limit of degree = 2 interactions used
Discussion Use cross-validation or GCV to determine the optimal degree and number of terms (k) for the given the degree degree = 1 no interaction terms degree = 2 interaction terms The final model is simply an OLS model where the terms have been chosen via the MARS algorithm. Thus MARS models are more interpretable than some models like neural networks and tree-based models.