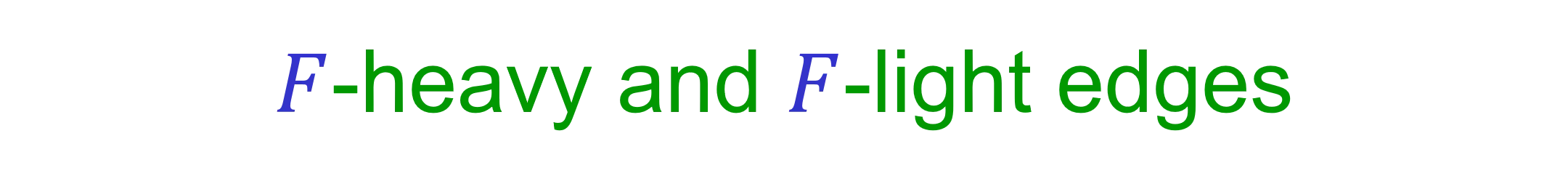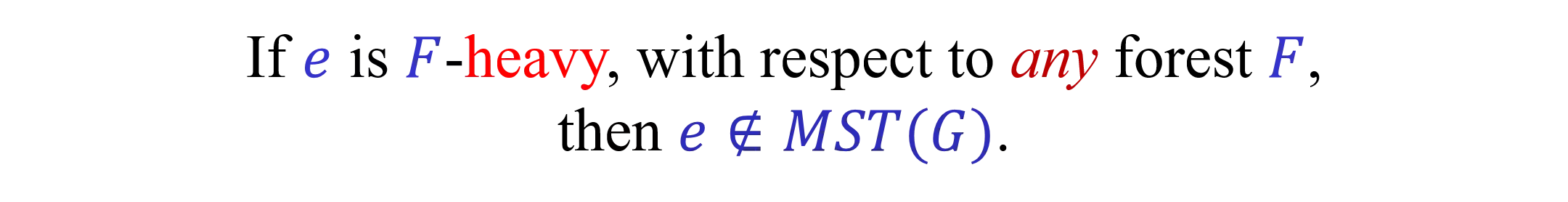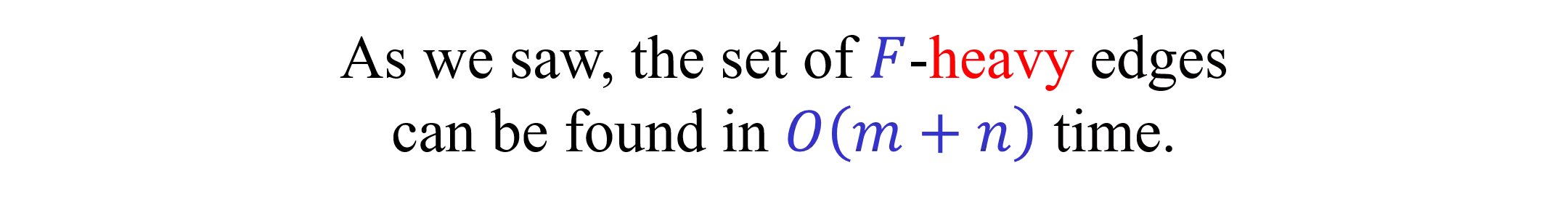Minimum Spanning Trees

This content discusses a randomized linear time algorithm developed by Uri Zwick from Tel Aviv University in 2015 for finding minimum spanning trees. The algorithm focuses on identifying heavy and light edges within a forest, using the concepts of -heavy and -light edges and a sampling lemma. It also presents a proof and insights on how the algorithm works efficiently.

• Randomized Algorithm
• Minimum Spanning Trees
• Linear Time
• Uri Zwick
• Sampling Lemma

prin_549 Follow

Uploaded on Feb 20, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Minimum Spanning Trees Randomized Linear Time Algorithm Uri Zwick Tel Aviv University October 2015 Last updated: November 18, 2015 1

2. ?-heavy and ?-light edges Let ? be a forest of ? = (?,?,?). We assume that all edge weights are distinct. Let ??(?) be the weight of the heaviest edge on the (unique) path in ? that connects the two endpoints of ?. If there is no such path then ??? = + . An edge ? is ?-heavy iff ? ? > ??? . An edge ? is ?-light iff ? ? ??? . As we saw, the set of ?-heavy edges can be found in ? ? + ? time. If ? is ?-heavy, with respect to any forest ?, then ? ???(?). 2

3. A randomized algorithm the idea [Karger (1993)] [Karger-Klein-Tarjan (1995)] Let 0 < ? < 1. E.g., ? =1 2. Let ??be a random subgraph of ? that contains each edge of ? independently with probability ?. Recursively compute ? = ???(??). Find the ?-heavy edges of ? and remove them from ?. Let ? be the resulting graph. Recursively compute and return ???(? ). 3

4. A sampling lemma [Karger-Klein-Tarjan (1995)] Let ??be a random subgraph of ? that contains each edge of ? independently with probability ?. Let ? = ???(??). Lemma: The expected number of edges of ? that are ?-light is at most ?/?. The bound on the expected number of ?-light edges is linear in ? and does not depend on ? ! 4

5. Proof of sampling lemma [KKT (1995)] Algorithm Sampling-Lemma-Proof( ? = (?,?,?) ): Assume ? ?1 < ? ?2 < < ?(??) Initialize ? ,?,? For ? 1 to ?: With prob. ?, let ? ? ?? If ??connects different trees of ?: Let ? ? {??} If ?? ? , let ? ? {??} This modification of Kruskal s algorithm generates a subgraph ??= (?,? ), ? = ???(??), and ?, the set of ?-light edges. 5

6. Proof of sampling lemma [KKT (1995)] For ? 1 to ?: With prob. ?, let ? ? ?? If ??connects different trees of ?: Let ? ? {??} If ?? ? , let ? ? {??} Whenever an edge is added to ?, with probability ? the edge is also added to ?. ? > ? ? = ? ? ? ? ? ? ? < 6

7. A randomized algorithm [KKT (1995)] The ?/? bound on the number of light edges is fantastic, but it only helps if ? is large enough. To make progress even if ? is not too large, we introduce Bor vka steps. 7

8. A randomized algorithm [KKT (1995)] Algorithm Rand-MSF( ? = (?,?,?) ): If ? = return ? ,? Bor vka(?,2) ?1 Rand-Subraph(? ,1/2) ?1 Rand-MSF(?1) ?2 Light-Edges(? ,?1) ?2 ? ? ,?2,? ?2 Rand-MSF(?2) return ? ?2 8

9. Analysis [KKT (1995)] When run on G = (?,?), the algorithm performs two recursive calls on ?1= (?1,?1) and ?2= (?2,?2). Let ? = |?|, ??= |??|, ? = |?|, ??= |??|. ? ?,? = ? ? + ? + ? ?1,?1 + ? ?2,?2 ?,? ?2,?2 ?1,?1 ?[?1] ? ?1 ? ?[?2] ?/4 ?1 ? 1/2=? 2 2 4 4 9

10. Analysis [KKT (1995)] ? 2,? ? 2,? ? ?,? = ? ? + ? + ? + ? 4 4 Claim: ? ?,? 2? ? + 2? Proof by induction: ? 2+? ? 2+? ? ?,? = ? ? + ? + 2? + 2? 2 2 = 2? ? + 2? Exercise: Is the analysis rigorous? Why can we replace ?1,?1,?2,?2by the expectations? 10

11. Bonus material Not covered in class this term Careful. We don t want to learn from this. (Bill Watterson, Calvin and Hobbes ) 11

12. Sampling lemma - Alternative version [Chan (1998)] Let ??be a random subgraph of ? that contains ? random edges of ?. Let ? = ???(??). Lemma: The expected number of edges of ? that are ?-light is at most ??/?. (The subgraph ??now has a fixed number of edges.) (This slightly simplifies the analysis of the algorithm.) Note that ?? ?=? ? ?. ?, where ? = 12

13. Proof of alternative version Backward analysis [Chan (1998)] Let ? ? be a random subset of size ?. Let ? = ???(?), ? = ??? ?(?,?). , ? = ????(?) (independent of ?). ? ? = ?Pr ? ? ? ? ? ???(? {?}) Idea: Instead of choosing ? and ? separately, let us first choose ? = ? {?}, and then choose ?,?. ? Pr ? ? = Pr ? ??? ? ? Since ? is a random item of ?, which is of size at least ?, and ??? ? is of size at most ?.

14. Proof of alternative version Backward analysis [Chan (1998)] ???? ?,? ???? ?,? + 1 , , with prob. ?/? with prob. 1 ?/? ? = ? = ????(?) ? , if ? = ? otherwise ? = ? {?} , Claim: ? is a random item of ?, ? is a random subset of ? of size ?, ? ? = ?, and ? and ? are independent. Exercise: Prove the claim. 14