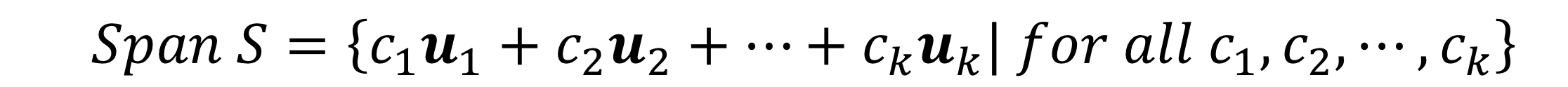Linear Algebra Summary and Solutions

This content delves into the concept of spans in linear algebra, discussing vector sets, generating sets, linear combinations, and solution spaces. It explores the span of vectors, linear independence, and the existence of solutions in a system of equations. The visual aids provided help in understanding the theoretical concepts presented.

• Linear Algebra
• Solutions
• Vector Spaces
• Spans
• Linear Independence

oliwia Follow

Uploaded on Aug 28, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

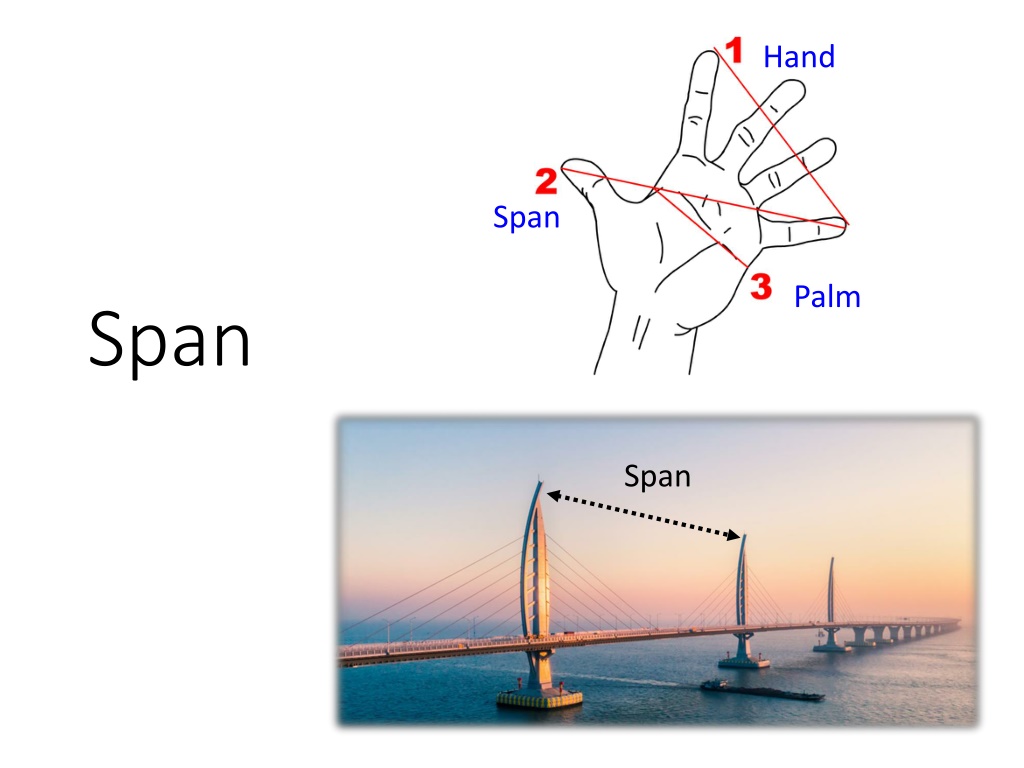
1. Hand Span Palm Span Span

2. Span A vector set ? = ?1,?2, ,?? S??? ? is the vector set of all linear combinations of ?1,?2, ,?? ???? ? = ?1?1+ ?2?2+ + ????| ??? ??? ?1,?2, ,?? Vector set ? = ???? ? ? is a generating set for ? or ?generates V One way to describe a vector set with infinite elements

3. 0 0 =0 Span ?1 0 Let ?0= {0 Ans: {0 0}, what is Span ?0? 0} (only one member) Span ?1 1 1 1 Let ?1= { 1}, what is Span ?1? Span ?1= { 1, If S contains a non zero vector, then Span S has infinitely many vectors 1 2, 1 2 , } 1

4. Span 1, 2 1 1 Let ?2= { what is Span ?2? } Let ?1= { Span ?1=? 1} 2 Span ?2 Span ?1 2 2 1 1 1 1 Span ?1= Span ?2 (Different number of vectors can generate the same space.)

5. Span 1, 2 1 ,2 Let ?3= { 1}, what is Span ?3? 2 Every vector in R2 is their linear combination 2 2 2 1 1 1 = R2 Span ?3

6. Span 1, 1 1, 2 1 ,2 1, 2 1 ,2 Let ?4= { what is Span ?4=? Let ?3= { what is Span ?3=? } 1} 3 2 2 1 3 2 2 2 2 2 1 2 1 1 1 1 1 Span ?3= R2 Span ?4= R2

7. Has solution or not? The same question ?11 ??1 ?12 ??2 ?1? ??? Is ? the linear combination of columns of ?? ?1 ?? ?1 + ?2 + + ?? = The same question ?11 ??1 ?12 ??2 ?1? ??? ?1 ?? Is ? in the span of the columns of ?? ???? ,

8. Span Every b has solution 1 2 1 2 2 2 1 1 1, 2 1 ,2 Let ?3= { 1}, what is Span ?3? 2 Every vector in R2 is their linear combination 2 2 2 1 1 1 = R2 Span ?3

9. Summary ? ?? ? ?? ?:? ? Is ? in the span of the columns of ?? Is ? a linear combination of columns of ?? YES NO The columns of ? are independent. The columns of ? are dependent. No solution Rank A = n Rank A < n Nullity A = 0 Unique solution Nullity A > 0 Infinite solution