Kinematics and Motion Equations
Learn about kinematics, motion graphs, distance calculations, acceleration, and free fall physics. Explore scenarios of cars accelerating, braking, and falling objects under gravity. Understand how to apply equations to calculate distance, velocity, and acceleration in various motion situations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Kinematics AND OTHER GOODIES
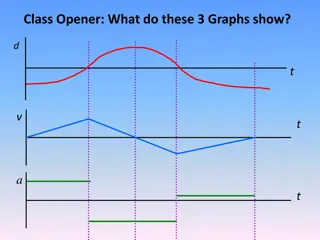
Do now: Which two graphs represent the same motion?
A car is traveling at 30 m/s for 10 seconds. How far does he travel? d = v * t d = 30m/s * 10s d = 300 m What if, however, the car is accelerating while it is traveling? How then, can we find how far it traveled?
Motion: How can we describe your motion? To use these equations we will need to have constant acceleration! Which we will in regents physics yay!
A car is at rest at a stop light. When the light turns green the car accelerates uniformly at 2 m/s2 for 10 seconds. How far does he travel in those 10 seconds? Useful formulas: Vf = vi + at Given At rest means vi = 0 m/s a = +10 m/s2 t = 10 s d = ? d = vit + (1/2) at2 Vf2 = vi2 + 2ad
A car initially moving at 25 m/s sees a stoplight and instantly presses on the breaks. The car begins to slow down uniformly at a rate of 5m/s2. How far does the car travel before it comes to a full stop?
A car initially moving at 30 m/s sees a wall125m away, the driver takes a second to press on the breaks. Upon hitting the breaks, the car begins to slow down uniformly at a rate of 5m/s2. Does the car hit the wall?
Free fall and the power of gravity All objects allowed to fall freely will experience an acceleration of 9.81 m/s2 when near the surface of the earth. Other planets may have different accelerations due to gravity. For example: The moon has an acceleration of 1.67 m/s2 We will assume there is no air resistance when conducting these problems unless otherwise told. ONLY CONCEPTUAL There will be two types of problems, either an object it thrown upwards or the object is allowed to fall freely. When the object is at its highest point, for that instant, the velocity of the object will be 0 m/s.
Examples Upton Chuck is riding the Giant Drop at Great America. If Upton free falls for 2.60 seconds, what will be his final velocity and how far will he fall? Draw a picture and label givens and directions Answers: d = 33.1 m and vf= 25.5 m/s
Examples A feather is dropped on the moon from a height of 1.40 meters. The acceleration of gravity on the moon is 1.67 m/s2. Determine the time for the feather to fall to the surface of the moon. Answer: t = 1.29 s
Examples A race car accelerates uniformly from 18.5 m/s to 46.1 m/s in 2.47 seconds. Determine the acceleration of the car and the distance traveled. Answers: a = 11.2 m/s/s and d = 79.8 m
Examples If Michael Jordan has a vertical leap of 1.29 m, then what is his takeoff speed and his hang time (total time to move upwards to the peak and then return to the ground)? Answer: vi= 5.03 m/s and hang time = 1.03 s (except for in sports commericals)
Examples A bullet leaves a rifle with a muzzle velocity of 521 m/s. While accelerating through the barrel of the rifle, the bullet moves a distance of 0.840 m. Determine the acceleration of the bullet (assume a uniform acceleration). Answer: a = 1.62*105m/s/s
Examples A baseball is popped straight up into the air and has a hang-time of 6.25 s. Determine the height to which the ball rises before it reaches its peak. (Hint: the time to rise to the peak is one-half the total hang-time.) Answer: d = 48.0 m