Implicit Model and Sorting Data Complexity Analysis
The content discusses the implicit model atomic elements, CPU registers, XOR operations, memory handling, and complexities associated with sorting data comparisons and movements. It explores implicit techniques like the fundamental trick for encoding integers, search tree structures, and cache-oblivious properties. The narrative also delves into implicit merging in algorithms like MergeSort, offering insights into efficient data organization.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
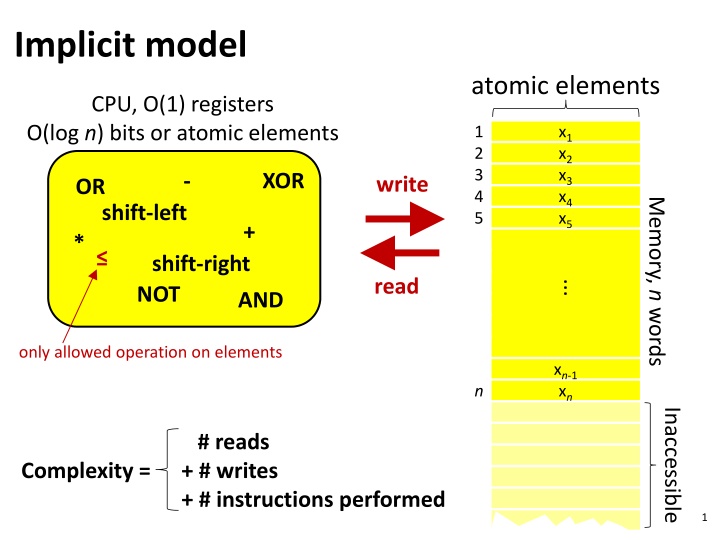
Implicit model atomic elements CPU, O(1) registers O(log n) bits or atomic elements 1 2 3 4 5 x1 x2 x3 x4 x5 - XOR write OR Memory, n words shift-left + * shift-right read ... NOT AND only allowed operation on elements xn-1 xn n Inaccessible # reads + # writes + # instructions performed Complexity = 1
Sorting Data Comparisons O(n log n) O(n2) O(n log n) O(n log n) moves/writes O(n log n) O(n) O(n) O(n) Implicit Yes Yes No Yes HeapSort SelectionSort Implicit priority queue SearchTree [FG05] [G. Franceschini, V. Geffert, An in-place sorting with O(n log n) comparisons and O(n) moves, J.ACM, 52(4), 515-537, 2005] Search trees Cache- oblivious No No No Yes Yes Search & updates O(log n) O(log n) O(log n) O(log n) O(log n) Range searching O(log n + t) O(log n + t) O(log n + t) - O(log n + t) Implicit No Yes Yes Yes No am. Red-black, ... (no updates) Sorted array [FG02] [FG03] [BFJ02], ... [G. Franceschini, R. Grossi, Optimal Cache-Oblivious Implicit Dictionaries, Proc. 30th International Colloquium on Automata, Languages, and Programming, volume 2719 of Lecture Notes in Computer Science, 316-331, Springer-Verlag, 2003.] [G. Franceschini, R. Grossi, J.I. Munro, L. Pagli. Implicit B-trees: New results for the dictionary problem. IEEE Symposium on Foundations of Computer Science, 145-154, 2002] [G.S. Brodal, R. Fagerberg, R. Jacob, Cache-Oblivious Search Trees via Binary Trees of Small Height, 13th Annual ACM- SIAM Symposium on Discrete Algorithms, 39-48, 2002] 2
The foundamental implicit trick The relative two elements x < y, can encode a bit x y = 0 = 1 y x 2log n elements can encode integer {0,...,n-1} 3
Search & updates O(log2n) Range searching O(log2n + t) Implicit Yes Search trees [J. Ian Munro, An Implicit Data Structure Supporting Insertion, Deletion, and Search in O(log n) Time, Journal of Computer and System Sciences, 33(1), 66-74, 1986] Each nodes stores ..2 -1 elements encoding the below fields ( =8 log n+2) Red-black search tree x x x x x x encodedby #elements 2 log n field values left (address) 0,1,..., n-1 x x x x x x x x x x x right (address) 0,1,..., n-1 2 log n parent(address) 0,1,..., n-1 2 log n color (red/black) 0,1 2 node size s 0,1,...,n-1 2 log n x x x x x x psmod s = 0 ps-3 =qs-3 root p2 -1 =q2 -1 ps qs ps-1 qs-1ps-2 qs-2ps-4 qs-4 s s s-1 s-2 s-4 xxxxxx xxxxxx xxxxx xxxx xx root p2 -1,q2 -1,... ,p ,q gap gap gap gap gap (2 +1) log n Total gap: 2 +(2 -1)+ + s (1 + # size-s-nodes) 4 = arbitrary elements
Implicit merging O(n + m) can be used in an implicit O(n log n) MergeSort 2 4 5 7 9 11 3 6 8 14 n m 2 3 4 5 6 7 8 9 11 14 5