Geometry Standards of Learning Practice Problems
Explore practice problems related to Geometry Standards of Learning (SOL), covering topics such as symbolic representation of arguments, laws of detachment, contrapositive, syllogism, counterexamples, and geometric proofs. Test your understanding of angles, lines, transversals, and congruence to strengthen your geometry skills.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Using Student Using Student Performance Performance Analysis Analysis Geometry Standards of Learning Standards of Learning 1
Practice for SOL G.1 Let m represent: Angle A is obtuse. Let n represent: Angle B is obtuse. Which is a symbolic representation of the following argument? Angle A is obtuse if and only if Angle B is obtuse. Angle A is obtuse or Angle B is obtuse. Therefore, Angle A is obtuse and Angle B is obtuse. m n m n m n B. m n m n m n m n m n C. m m n n D. m m n n A.
Practice for SOL G.1 Example of the law of detachment: Let p= a dog eats bread Let q= the dog gains weight p q, If a dog eats bread, then the dog gains weight is a true statement. John s dog eats bread. What can be concluded?
Practice for SOL G.1 Example of the law of contrapositive: Let p= a dog eats bread Let q= the dog gains weight p qmeans If a dog eats bread, then the dog gains weight. p q is a true statement. What is the contrapositive of this statement? Is it a true statement?
Practice for SOL G.1 Example of the law of syllogism: Let p= a dog eats bread Let q= the dog gains weight Let r= the dog gets fat p qmeans If a dog eats bread, then the dog gains weight. q rmeans If the dog gains weight, then the dog gets fat. Using the law of syllogism, what is the logical conclusion?
Practice for SOL G.1 Example of a counterexample: Let p= n is an integer and n is divisible by 4 Let q = n is divisible by 4 p qmeans If n is an integer and n is divisible by 4, then n is divisible by 4. A counterexample is any example that will prove a statement false. In this case, a number for which p is true and q is false is a counterexample. What is a counterexample to p q ?
Practice for SOL G.2 Lines aand b intersect lines c and d. c d a 1 b 2 6 4 3 5 Which statement could be used to prove a band c d? A. 1 and 2 are supplementary and 5 6 B. 1 3 and 3 5 C. 3 and 5 are supplementary, and 5 and 6 are supplementary D. 3 4 and 2 6
Practice for SOL G.2 This figure has more than one transversal and markings to indicate congruent angles. Which statement about the figure shown must be true? c A. Only a ll b B. Only c ll d C. Both a ll b and c ll d D. No lines are parallel. d a b
Practice for SOL G.2 This figure has more than one transversal. Two angle measurements are shown. (Figure is not drawn to scale.) Based only on the information given, which statement about the figure shown must be true? c 87 87 d A. Only all b B. Onlycll d C. Bothall bandcll d D. No lines are parallel. a b
Practice for SOL G.2 In the figure shown, line c and line d are cut by a transversal. (Figure is not drawn to scale.) (2 (2x + 40) + 40) c d (6 (6x + 20) + 20) For what value of xwill linec be parallel to line d ? A. B. C. D. 5 5 15 15 20 20 30 30
Suggested Practice for SOL G.2a Given: all c x 85 105 What is the value of x ? 85 Isbll c ? Why or why not? Isdll e ?Why or why not?
Practice for SOL G.2a c b Given: all b and dll e a d Find the values of x, y, andz. 107 117 x z e y
Practice for SOL G.3 Line a passes through points with coordinates (-4, 5) and (2, -2). What is the slope of a line perpendicular to line a? Slope of perpendicular line =
Practice for SOL G.3 Find the coordinates of a point that lies on a line which passes through point P and is parallel to line c. c Find the coordinates of a point that lies on a line which passes through point P and is perpendicular to line c. P
Practice for SOL G.3 1. Find the coordinates of a point on the graph that lies on a line which passes through point Nand is parallel to line a. Use this graph to answer the questions. All points have integral coordinates. 2. Find the slope of a line which passes through point Nand is perpendicular to line a. N 3. The coordinates of a point that lies on a line which passes through pointNand is perpendicular to line aare represented by . What is the value of the y-coordinate? a ?,?
Practice for SOL G.3 Given: Triangle ABC with vertices located at A(1, 1), B(2, -3), and C(-1, -4). Triangle ABCwill be reflected over the line y = x. What will be the integral coordinates of point C' after this transformation?
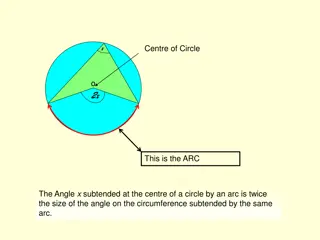
Practice for SOL G.4 Arcs WX and YZ are drawn using the same radius. An arc with radius WX is centered on point Y and intersects arc YZ at point Z. A line segment will connect points D and Z. Which statement justifies this construction? A. A Dbecause they are corresponding parts of congruent triangles. B. A Dbecause they are alternate interior angles. C. A Dbecause AB = DE.
Practice for SOL G.5 Given: Triangle ABC with AB = 42 and BC = 20 Which of the following are possible lengths for AC? 12 20 22 32 42 50 62 70
Practice for SOL G.6 Given: In the figure, line segments AC and BD bisect each other at point E. Prove: AED CEB
Practice for SOL G.6 Students need additional practice proving triangles congruent using algebraic methods. Given: MNO and STV are isosceles. m N = (2x 28) m T = (x + 22) N T S V M O What measure of S could be used to prove A50 B 54 C 65 D 72 MNO STV ?
Practice for SOL G.7 Given:MNO and VTS Select two relationships that together would proveMNOVTS by the Side-Angle-Side (SAS) Similarity Theorem. ~ N T N T M S M V MN SV ST MO MN MO VT VS = = M O S V
Practice for SOL G.7 Select each set of numbers that could represent the side lengths ofMNO. ~ Given:MNOSTV N T 7, 6, 2.5 7, 6, 2.5 16, 13, 5.5 16, 13, 5.5 21 21 18 18 14, 12, 7 14, 12, 7 2.1, 1.8, 1.05 2.1, 1.8, 1.05 M O 10.5, 9.5, 5.5 10.5, 9.5, 5.5 4.2, 3.6, 2.1 4.2, 3.6, 2.1 S V 10.5 10.5
Practice for SOL G.8 A ladder leans against a wall. The bottom of the ladder is 10 feet from the base of the wall, and the top of the ladder makes an angle of 25 with the wall.Find the length, x, of the ladder.
Practice for SOL G.9 Sasha built a window for her dollhouse in the shape of a quadrilateral. She knows the opposite sides of the window are parallel but she wants to be sure it is in the shape of a rectangle. Which of these can she use? A. The consecutive angles of the window are supplementary. B. The opposite sides of the window are congruent. C. The diagonals of the window bisect each other. D. The diagonals of the window are congruent.
Practice for SOL G.9 Andy inscribed quadrilateral ABCD in a circle. Line segment BD is a diameter of the circle. Based on this information, select each statement that must be true. Line segment AC is a diameter of the circle. Angle C is a right angle. The sum of the measures of B and D is 180 180 . The sum of the measures of A and B is 180 180 .
Practice for SOL G.10 Which of these regular polygons could tessellate a plane? Square Pentagon Octagon Hexagon Decagon
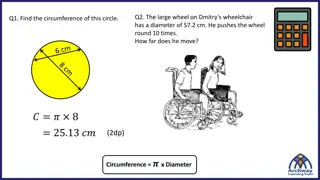
Practice for SOL G.11 Given: Circle Mwith secants ABandAC m A = 30 If the length of arcBCis 3 cm, what is the circumference of the circle?
Practice for SOL G.11 Find the area of the shaded sector of Circle Q. A B 60 8 cm Q Find the length of arc AB.
Practice for SOL G.11 This figure represents a design for a stained glass window. The window is divided by chords MN and ST. S 1. What is the value of x? M 10 8 2. What is the length of ST? 4 N x - 4 T
Suggested Practice for SOL G.11 Students need additional practice solving real-world problems using properties of circles. Circle M represents a circular race track. The radius of this race track is 120 feet. Juan will start at point A and run in a clockwise direction to point B. Angle AMB measures 55 . A Which is closest to the number of feet Juan will run from point A to point B? 55 55 ft 58 58 ft 115 115 ft 120 120 ft D. B 55 55 120 120ft A. B. C. M
Practice for SOL G.11 Bob divides his circular garden into 10 congruent sectors to plant different types of flowers. The circumference of Bob s garden is 50.5 feet. What is the area of one sector of Bob s garden?
Practice for SOL G.12 The coordinates of the center of a circle are (-2, 6). This circle has a diameter of 10 units. a) What is the equation of the circle? b) Give the integral coordinates of two points that lie on the circle.
Practice for SOL G.12 A circle has a center at (-1, 4) and a diameter of 20. Select each pair of coordinates that represent a point on this circle. (-7, -4) (11, 20) (19, 16) (5, 12) (-9, -2) (-1, 4)
Practice for SOL G.12 Write the equation of a circle, in standard form, that has a diameter with endpoints at and .
Practice for SOL G.12 Which of these points lie on the circle represented by this equation?
Practice for SOL G.12 The equation of a circle is (x - 3) + (y + 4) = 16. a) What are the coordinates of the center of the circle? b) What is the radius of the circle? c) What is the diameter of the circle? d) Give the integral coordinates of two points that lie on the circle.
Practice for SOL G.13 A statue consists of a square pyramid and a rectangular prism with congruent bases. Specific measurements of the statue are shown in this figure. Slant height can be found using the Pythagorean Theorem: 3 + x =5 x= 4 5 5 in x 10 10 in 6 6 in 6 6 in What is the total surface area of the statue represented by this composite figure? [Figure is not drawn to scale.]
Practice for SOL G.13 What is the volume of this figure rounded to the nearest cubic inch? The height, a, can be calculated using the Pythagorean Theorem, where 3 is half the length of the base and 4 is the slant height: 5 5in a 10 10in 6 6in 6 6in
Practice for SOL G.14 A rectangular prism has a volume of 36 cm . a) If the height of the prism is tripled and the other dimensions do not change, what is the volume of the new rectangular prism? b) If all dimensions of the original rectangular prism are tripled, what is the volume of the new rectangular prism?
Practice for SOL G.14 Two similar rectangular prisms have side lengths with a ratio of 1:3. What is the ratio of their surface areas? What is the ratio of their volumes?
Practice for SOL G.14 The dimensions of a triangular prism with a surface area of 51.46 cm are multiplied by a scale factor of 2.5 to create a similar triangular prism. What is the surface area of the new triangular prism? Extension: What is the relationship between the volume of the original prism and the volume of the new prism?
Practice for SOL G.14 Cathy has two cylinders that are the same height, but the volume of the second cylinder is 16 times the volume of the first cylinder. The radius of the second cylinder is A. 2 times the radius of the first cylinder. B. 4 times the radius of the first cylinder. C. 8 times the radius of the first cylinder. D. 16 times the radius of the first cylinder.
Practice for SOL G.14 Cathy has two cylinders with radii the same length, but the volume of the second cylinder is 16 times the volume of the first cylinder. The height of the second cylinder is A. 2 times the height of the first cylinder. B. 4 times the height of the first cylinder. C. 8 times the height of the first cylinder. D. 16 times the height of the first cylinder.
Practice for G.14 Given: Objects A and B are three-dimensional. Object A is similar to object B. The height of object A is 24 24 inches and the height of object B is 36 36 inches. 1. What is the ratio of the surface area of object A to the surface area of object B in simplest form? 2. What is the ratio of their volumes in simplest form?
Practice for G.14 Pyramid S is similar to Pyramid T. If the ratio of the volume of Pyramid S to Pyramid T is 64:125 64:125, complete the table by finding the ratio of their side lengths and the ratio of their surface areas. Pyramid S Pyramid T Side Length to Surface Area to 64 64 125 125 Volume to
Practice for G.14 The ratio of the surface areas of two spheres is 1:9 1:9. 1. What is the ratio of the lengths of their radii? What is the ratio of their volumes? 2. If the volume of the smaller sphere is 64 is the volume of the larger sphere? 64 cubic inches, what
Practice for SOL G.14 A cylinder has a surface area of 96 square inches. If all dimensions of this cylinder are multiplied by to create a new cylinder, what will be the surface area of the new cylinder? 1 2
