Exploring Gravitational Quantum States of Antihydrogen
The research delves into the intriguing realm of gravitational quantum states of antihydrogen, posing questions about the feasibility of gravitational mass extraction from these states. Through topics like spectroscopy, interference, and time-spatial resolution, the study sheds light on the properties and quantum reflection phenomena of antihydrogen states in a gravitational field. The effects of surface interactions, Casimir-Polder potential corrections, and annihilation are explored, offering insights into the behavior and challenges in observing gravitational states.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
GRANIT 2014 Gravitational Quantum States of Antihydrogen A. Voronin, V. Nesvizhevsky, P.Froelich O.Dalkarov, E.Kupriyanova
Plan of the talk Gravitational states of antihydrogen: Is it possible? How can we get gravitational mass out of gravitational states? Properties of gravitational states Spectroscopy, interference and time-spatial resolution of gravitational states
Gravitational quantum states? State of motion of a quantum particle, which is localized near reflecting surface in a gravitational field of the Earth. 2 d dx + = = F( ) 0, (0) F 0 x x ( ) Ai x 2 n E, peV 2.7 1.4 Z, m 13.7 24.0
Gravitational states of Antihydrogen: Seems Impossible? Quantum Reflection! 10 m = % Red- silica, black- gold 0.01cm = % 10 m = % 0.01cm = % 0.1cm = % 0.1cm = % 1cm = % 1cm = % 10cm = % 10cm = % G. Dufour, A. G rardin, R. Gu rout, A. Lambrecht, V. V. Nesvizhevsky, S. Reynaud, A. Yu. Voronin Phys. Rev. A 87, 012901 (2013)
Gravitational states of antihydrogen Quantum reflection is about 97% - it works like a reflecting wall 2 2 d + = ( ) z 0 Mgz E 2 2 d + + = 2 ( ) z ( ) z 0 2 V Mgz E m dz CP 2 2 m dz (0) '(0) a = 0.005 i CP l = ( ) 0 E, peV g = ( ) z Ai( / )/ |Ai'( )| z l g n n a 2.7 2/3 0.005 1 CP l 3 1 2 (2 ) n n 4 g 1.4 Z, m 13.7 24.0
Effects of surface Hierarchy of scales : gravity and surface-atom interaction are factorized Annihilation in the bulk of the wall: short range atom-wall interactions are washed out Small annihilation width of gravitational states: compromise between long life-time and observation | | l a g CP
Correction by Casimir-Polder potential + annihilation Mgz 2 d dx + = (x) 0 x z V(z) n 2 l | |/ a 0.005 (0) '(0) a = 0.005 i CP l 0 g Correction by Casimir-Polder and annihilation: = + = + / a l = n n g ( Re / ) 2 Im / a l a l 0 0 n n g g l = = g 0.1 s 2 Im 2 Im a Mg a g All states have equal shift and lifetime~0.1s No surface effects in transition frequiencies
Gravitational states and Gravitational mass = = = Classical: 2 / mz Mg z g T H g 2 2 2 d d dx + = + = Quantum: ( ) z 0 F( ) 0 Mgz E x x n 2 2 2 m dz 2 2 2 2 M g m = = -12 -6 = =0.61 10 eV; 5.87 10 l m 3 3 g g 2 2 Mmg 1 l = = = (z) ( / / ) E z l x F z l E n g n g n g n g g 2 2 l 2 H g = = g 2; m M = = = g or T M m 2 g g l gl g g g Gravitational states are all about energy and spatial scales
Methods of observation Spectroscopy: induced transition between gravitational states Interference: temporal and spatial oscillations of annihilation signal of superposition of gravitational states Time and spatial resolution of free-fall events: mapping of momentum distribution of gravitational state into time-of-fall or spatial distribution
Spectroscopy- to induce transitions between gravitational states with alternating magnetic field Developed for neutrons by V. Nesvizhevsky, S. Baessler, G. Pignol, K. Protassov, A.Voronin E Z, m 13.7 24.0
Antihydrogen in Magnetic Field Effective Stark-effect HF splitting Coulomb Center-of-mass fall Field-magnetic moment interaction E d F=1, M=1 F=1, M=0 c b F=1, M=-1 a F=0, M=0 B
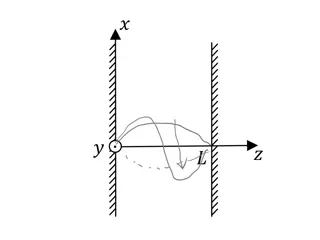
Possible scheme of flow-throw experiment B 5 3 4 Hd 1 Ha v 2 L 1-source of ultracold antihydrogen, 2-mirror, 3- absorber, 4- magnetic field, 5- detector 1 / , 15 , 25 a d v m s H m H = = = , 10 , 10 / , 30 m B Gs Gs m L cm 0
Transition probability 2 ik 1 2 t = + 2 2 ik 2 2 sin ( )exp( t) P ik + 2 ik 2 2 + 3 g ( ) l = B p ik 2 ( ) z z k i P 0.5 0.4 0.3 0.2 0.1 Hz 800 820 840 860 Transition probability as a function of frequency. Transition 1->5 Time of observation t=0.1 s
EP and gravitational mass 2 2 2 M g m -12 = =0.61 10 eV 3 g 2 2 2 2 3 ik 2 M g m m ( ) = = M 3 ( ) ik k i 3 2 2 g k i 3 ik 2 = = M m M 3 2 ( ) g k i PRECISION 3 N = 2 ; 10 N H 2 H 3 10 1 5
Interference of gravitational states N = C i i = 1 i * ( , ) z t dz ( , ) z t dz i d d = * ( , ) j z t ( , ) z t ( , ) z t 2 m dF dz E E ( ) = ) 1 cos( exp( ) = t t 12 2 1 1 0.1s 12 12 dN dt 20 15 10 5 t, ms 20 40 60 80 100
Time and Spatial Resolving of Gravitational States Momentum distribution of gravitational state can be mapped into measurable time or spatial distribution P 0.5 0.4 0.3 0.2 0.1 Ha m s 0.04 0.02 0.02 0.04 P 0.0020 0.0015 0.0010 0.0005 H=10cm m 0.010 0.005 0.005 0.010
Mapping of momentum distribution 1 = / ipz ( , ) z t ( , , ') G p t p F p dpdp ( ') ' e 0 2 it m = + 2 2 2 2 ( , , ') G p t p exp ( /3) ( ') p Mgpt M g t p Mgt p 2 2 m t gt m t 3 2 2 2 it M g imz + = + ( , ) z t ( ); ( ) e F p Mgt p z 2 2 t m 0 0 0 2 m t = 2 2 | ( , )| z t | ( )| F k 0 = = 1)z : ( ), ( 2 / g z z k mg t t t 0 0 0 0 ) m z z = = = 2) / : t t L v k 0 0 t 0
P P 0.5 0.35 0.30 ( ) n k 0.4 = 0.25 l 0.3 g 0.20 n 0.15 0.2 0.10 0.1 0.05 m s m s 0.04 0.02 0.02 0.04 0.04 0.02 0.02 0.04 velocity distribution 1 state 2 state P P 0.0020 0.0014 0.0012 0.0015 0.0010 0.0010 0.0008 0.0006 0.0005 0.0004 ms 141 142 143 144 145 ms 141 142 143 144 145 Time-of fall distribution H= 10 cm P P 0.0014 0.0020 0.0012 0.0010 0.0015 0.0008 0.0010 0.0006 0.0004 0.0005 0.0002 m m 0.010 0.005 0.005 0.010 0.010 0.005 0.005 0.010 Spatial distribution time-of-flight T=0.1s
Phase monitoring = + ( ) Exp i t 1 21 2 P P 0.0030 0.0020 0.0025 0.0015 0.0020 0.0010 0.0015 0.0010 0.0005 0.0005 ms ms 141 142 143 144 145 141 142 143 144 145 t = 0 = 0.0019 t s P P 0.005 0.004 0.004 0.003 0.003 0.002 0.002 0.001 0.001 ms ms 141 142 143 144 145 141 142 143 144 145 = = 0.0014 0.0029 t s t s
P 0.0030 0.0025 0.0020 0.0015 0.0010 0.0005 ms 141 142 143 144 145 B 3 4 1 Ha 2
Conclusions Gravitational states of Antihydrogen: simplest bound antimatter quantum system, determined by gravity. Effects of surface are canceled out. Gravitational states of Antihydrogen- metastable and long-living, easy to study due to annihilation signal Gravitational states- a way to precision measurement of the gravitational mass M