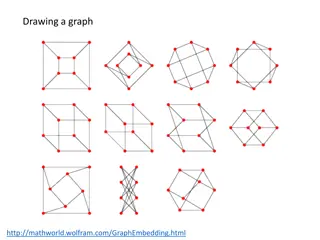
Exploring Graph Theory: From Knigsberg Bridge Problem to Traveling Salesman Problem
Delve into the realm of graph theory with a historical perspective on the Knigsberg Bridge Problem and advancements like the Traveling Salesman Problem. Uncover the foundations of non-directed graphs, Hamiltonian graphs, and their real-world applications.
Uploaded on Nov 27, 2024 | 0 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
GRAPH THEORY- VIRTUAL ROOM EDULAB KULAK Fabien Decruyenaere
THE K NIGSBERG BRIDGE PROBLEM Does there exist a walk that begins on one of the banks or islands, that takes each of the 7 bridges exactly once and that ends where you started?' ('Solutio Problematis ad geometriam situs pertinentis', Commentarii Academiae Scientiarum Imperialis Petropolitanae 8 (1736), pp. 128-140.)
ggbm.at ggbm.at/cYcV2UH4 cYcV2UH4
Definition 1.1 A (non-directed) graph G = (V, E) consistsofafinitenon-emptysetofpoints V ={v1, v2, . . . , vn} and a finite set of lines E E(V ), with E(V ) = { {vi, vj} | vi, vj V }. Definition1.2 A (non-directed) graph G= (V, E) consists of : 1. afinitenon-emptysetofpointsV; 2. a finite set of lines E; 3. a function : E e E : (e) {1, 2}. P(V ) such that 7
TRAVELING SALESMAN PROBLEM TRAVELING SALESMAN PROBLEM 20th of april, 2001 : David Applegate, Robert Bixby, Vasek Chvatal, William Cook : 15112 cities in Germany! Length : 1573084 = 66000km Total computer time = 22.6 years (Compaq EV6 Alpha Processor of 500MHz) May 2004 : 24978 cities in Sweden (72500 km) World record : 13th of March 2018 : Keld Helsgaun Length=7 515 772 107
HAMILTONIAN GRAPHS HAMILTONIAN GRAPHS Sir William Rowan Hamilton (1805-1865) Age of 7 : Hebrew Age of 13 : French, Italian,Arabian,Syrian,Sanskrit,Indian languages 1843 : quaternions THEOREM : If G is a connected simple graph with n 3 points and if for each point v deg(v) n/2, then G is Hamiltonian.
Definition 1.3 1. We call points v and w van een graaf G buren als er een lijn e bestaat die v en w verbindt (d.w.z. (e) = {v, w}); in dit geval zeggen we ook dat de lijn e haar uiteinden v en w verbindt of dat de punten v en w incident zijn met de lijn e. 2. De graad d(v) van een punt v is het aantal lijnen incident met v De grootste graad die in G (een lus telt hierbij voor twee). voorkomt, noteren we als (G) en de kleinste graad die in G voorkomt als (G). 15
2. ISOMORFE GRAFEN Definitie 2.1 Twee grafen G = (V, E) en H = (W, F ) heten isomorf als er bijecties f : V W en g : E F bestaan zo dat e E : G(e) = {v, w} H(g(e)) = {f (v), f (w)}. 17
1879 : Bewijs Kempe 1880 : Bewijs Tait 1890 : Fout bewijs Kempe 1891 : Fout bewijs Tait 1976 : Bewijs Appel en Haken