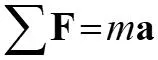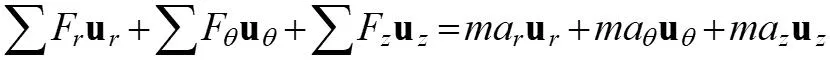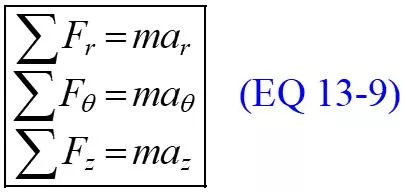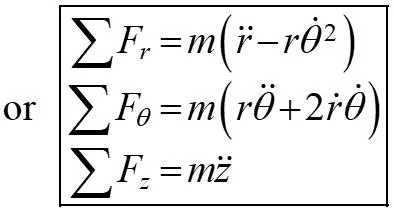Equations of Motion in Cylindrical Coordinates
Equations of motion in cylindrical coordinates can be expressed in terms of components or scalar equations. Practical applications include analyzing motion in various engineering systems. In-class practice problems involve dealing with spring forces and applying the chain rule to determine forces in specific positions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
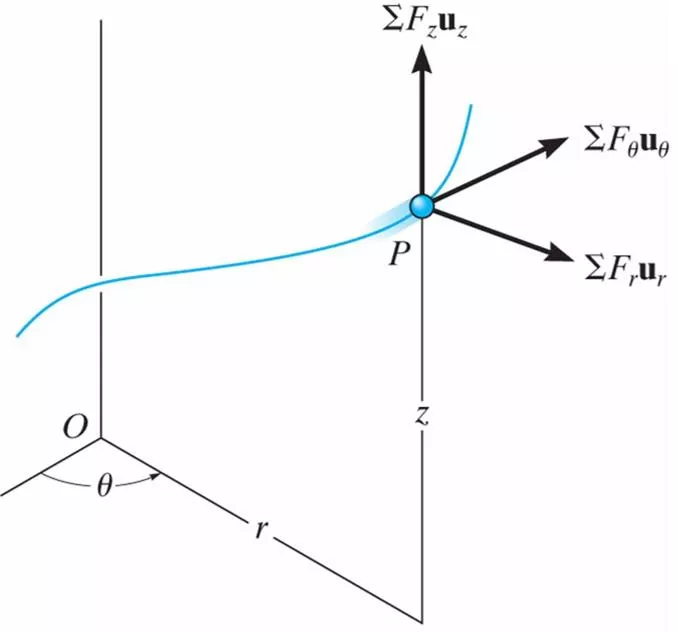
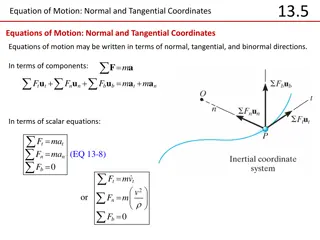
13.6 Equation of Motion: Cylindrical Coordinates Equations of Motion in Cylindrical Coordinates The equations of motion can also be written along cylindrical coordinates. F F F F + + = a m In terms of components: = + + u u u u u u ma ma ma r r z z r r z z Or as scalar equations: = = = F F F ma ma ma r r (EQ 13-9) z z ( ( ) = = = + F m r r 2 r ) or 2 F F m r mz r z
In-Class Practice Problem 1 Can you do this in n-t-b? Can you do this in r- -z? Apart from amusement park rides, what are some practical applications of this problem?
In-Class Practice Problem 2 13-85 The spring-held follower AB has a weight of 0.75 lb and moves back and forth as its end rolls on the contoured surface of the cam, where r = 0.2 ft and z = 0.1*sin(2 ) ft. If the cam is rotating at constant rate of 6 rad/sec, determine the force at the end A when = 45 . In this position the spring is compressed 0.4 ft. Neglect friction at the bearing C. Find FA when ? = 45 An actual r- -z problem! How to deal with spring force? Need to take time derivatives of r, ?, and z r = constant ? = constant ? = ?(?) Chain Rule!
13.4 Common External Forces Spring Forces Spring force is related to the deformation (deflection) of the spring by the equation: ( ) = s l l = = = = = s F ks spring stiffness force unit length stretch or deflection of spring deformed length undeformed length k s l l 0 0
In-Class Practice Problem 2 13-85 The spring-held follower AB has a weight of 0.75 lb and moves back and forth as its end rolls on the contoured surface of the cam, where r = 0.2 ft and z = 0.1*sin(2 ) ft. If the cam is rotating at constant rate of 6 rad/sec, determine the force at the end A when = 45 . In this position the spring is compressed 0.4 ft. Neglect friction at the bearing C. ??= ? ? ?0 When ? = 45 , ? ?0 = 0.4 ?? Want to get ? ??? ?0 in terms of z ? 45 = 0.1 sin 90 = 0.1 This means ? ?0 = z + 0.3 Thus, ??= ? ? + 0.3
In-Class Practice Problem 2 13-85 The spring-held follower AB has a weight of 0.75 lb and moves back and forth as its end rolls on the contoured surface of the cam, where r = 0.2 ft and z = 0.1*sin(2 ) ft. If the cam is rotating at constant rate of 6 rad/sec, determine the force at the end A when = 45 . In this position the spring is compressed 0.4 ft. Neglect friction at the bearing C. ? = ?(?) Chain Rule! ?? ??=?(??????) ? ??????? ?? ?? ??= 0.1 2 ? cos(2?) Evaluating with = 45 and ? = 0
In-Class Practice Problem 2 13-85 The spring-held follower AB has a weight of 0.75 lb and moves back and forth as its end rolls on the contoured surface of the cam, where r = 0.2 ft and z = 0.1*sin(2 ) ft. If the cam is rotating at constant rate of 6 rad/sec, determine the force at the end A when = 45 . In this position the spring is compressed 0.4 ft. Neglect friction at the bearing C.