Electric Flux and Analogies in Electromagnetism
Concept of electric flux, flux density, and surface flux in electromagnetism. Learn how to calculate flux through surfaces and understand the water analogy to visualize flux lines. Analogies with electric current and conducting mediums are also discussed. Delve into examples and analogies to deepen your understanding of these fundamental electromagnetic concepts.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
ECE 3318 Applied Electricity and Magnetism Spring 2024 Prof. David R. Jackson Dept. of ECE Notes 9 Flux Notes prepared by the EM Group University of Houston 1
Flux Density q From Coulomb s law: = r E 2 4 r 0 12 8.854187818 10 F/m E 0 Flux lines (Flux lines show us the direction of the electric field vector.) q Define: D E flux density vector 0 Charge in free space (This definition holds in free space.) We then have q = 2 2 [C/m ] D r 4 r 2
Flux Through Surface Define flux through a surface: E C n D ndS S Note: In this picture, flux is the flux crossing the surface in the outward sense. q S q = 2 2 [C/m ] D r 4 r Cross-sectional view Charge in free space 3
Example z Find the flux from a point charge going out through a spherical surface. n D D ndS r S q y = D r dS S S x q = r r dS 2 4 q r S = + n r = dS (We want the flux going out.) 2 4 r S 4
Example (cont.) 2 q = d d 2 sin r 2 4 r 0 0 q 2 = d d sin 4 0 0 2 q = sin d d 4 0 0 q ( )( ) 2 = 2 4 = [ ] q C 5
Current Analogy Conducting medium Analogy with electric current n A = J ndS I S A small electrode in a conducting medium spews out current equally in all directions. I S J I = 2 2 A/m J r 4 r Cross-sectional view 6
Current Analogy (cont.) Current Electric Flux J D Conducting medium Free-space I q I q = 2 2 [A/m ] J r = 2 2 [C/m ] D r 4 r 4 r C A D ndS = J ndS I S S 7
Water Analogy z Each electric flux line is like a stream of water. N streamlines Water streams Each stream of water carries Fn / N [m3/s]. S n F y x Water nozzle (omnidirectional) Fn =flow rate of water out of nozzle [m3/s] Fs =flow rate of water out of surface [m3/s] Note that the flow rate through a closed surface is Fs =Fn. 8
Water Analogy (cont.) Here is a real flux fountain (Wortham fountain, a.k.a. the Dandelion on Allen Parkway). 9
Water Analogy (cont.) Analogy example: ( ) = 3 15 m /s n F flow rate from central node ( ) N = 1000 number of pipes S ( ) N = 20 number of flux lines through surface S s Find Fs (flow rate through surface S) 3 15 m /s 1000 pipes ( ) 0.3 m /s = = 3 20pipes sF 10
Flux through a Surface using Flux Lines (Point Charge) z Example: E q = 15 C ( ) q N = 1000 number of flux lines y ( ) S N = 20 number of flux lines through surface S s Find (flux through surface S) x 15 C ( ) = = 20flux lines 0.3 C 1000 flux lines 11
Flux in 2-D Problems 2-D problems: Everything is infinite and not changing in the z direction. We now define the flux per meter in the z direction. E n D ndl C/m l C We can think of las being the flux through a surface S that is the contour C extruded one meter in the z direction. 0 l C 0 l Line charge in free space C = D ndS S 1 m S ( ) 1 m = = l l C 12
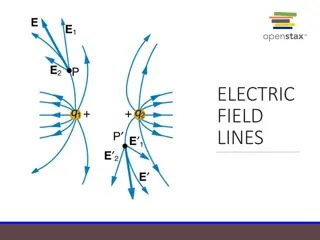
Flux Plot (2-D) Rules for a 2-D flux plot: 1) Flux lines are in the direction of the electric field*. 2) The magnitude of the electric field is inversely proportional to the spacing between flux lines**. 3) Flux lines come out of positive charges and end on negative charges (they cannot stop or begin in free space)***. y Flux plot for a line charge = * A convention we adopt. **A convention we adopt. *** A consequence of Gauss s law. 0 l E 2 0 x 0 l 13
Example Line charge Notice how the flux lines get closer as we approach the line charge: there is a stronger electric field there. l 0C/m y = 0 l E 2 0 According to rule #2: If W is the distance between flux lines: W x W This happens automatically in this example by choosing a fixed number of equally-spaced flux lines. 14
Flux Property in 2-D Flux Plots The flux (per meter) lthrough a contour is proportional to the number of flux lines that cross the contour. NC is defined as the number of flux lines through C. E n D ndl N l C C C Note: The constant of proportionality depends on how many flux lines you decide to draw. General E field Please see the Appendix for a proof of this flux property. 15
Example y l = 1 C/m 0 Goal: N = Choose: 16 f Graphically evaluate = D ndl C l C x 1 C/m 16 lines ( ) = 4 lines l 1 4 Note: = C/m The answer will be more accurate if we use a plot with more flux lines! l 16
Equipotential Contours An equipotential contour CV is a contour on which the potential is constant. y Line charge example E Flux lines 0 l x = 1 V Equipotential contours CV = 0 V = + 1 V 17
Equipotential Contours (cont.) Property: E C V The flux line are always perpendicular to the equipotential contours. C E V (proof on next slide) ( = constant ) 18
Equipotential Contours (cont.) Proof of perpendicular property: Proof: Two nearby points on an equipotential contour are considered. On CV : B = E dr V = 0 AB A B E dr C = 0 E r V A E = E r B E r r A Conclusion: The r vector (lying on CV) is perpendicular to the flux lines. 19
Method of Curvilinear Squares 2-D Flux Plot C V E V + Assumption: B Assume a constant voltage difference Vbetween adjacent equipotential lines in a 2-D flux plot. A Note: Along a flux line, the voltage always decreases as we go in the direction of the flux line. Curvilinear square Note: It is called a curvilinear square even though the shape may be rectangular. 20
Method of Curvilinear Squares (cont.) Theorem: The shape (aspect ratio L/W) of the curvilinear squares is preserved throughout the flux plot. Assumption: V is constant throughout plot. C V E + V E C V W L + V L W =constant 21
Method of Curvilinear Squares (cont.) Proof of constant aspect ratio property C B V E V = E dr = V V + AB A dr W B = dl dr L A If we integrate along the flux line, E is in the same direction as dr . E dr E dr = ( ) = o cos 0 E dl B = = V E dl V Hence, AB A B E dl V E L V so Therefore A 22
Method of Curvilinear Squares (cont.) Hence, V E = L C + V V E W Also, B L 1 Reminder: A E In a flux plot the magnitude of the electric field is inversely proportional to the spacing between the flux lines. W so 1 E = W C The constant C1 is some constant of proportionality. 1 Hence, 1 C L W = = V constant (proof complete) 1 23
Example Line charge y Notice how the flux lines get closer as we approach the line charge: there is a stronger electric field there. l 0C/m 1 1 E W x L W The aspect ratio L/W has been chosen to be unity in this plot. In this example L and W are both proportional to the radius . 24
Example A parallel-plate capacitor Note:L / W 0.5 25
Example Coaxial cable with a square inner conductor L W = 1 Figure 6-8 in the Hayt and Buck book (9th Ed.). 26
Making a Flux Plot Here are the rules for making a 2-D flux plot, assuming that we start with equipotential contours separated by a fixed value of V*: Rule 1: We start with equipotential contours having a fixed V between. Rule 2: Flux lines are drawn perpendicular to the equipotential contours. Rule 3: L / Wis kept constant throughout the plot. If all these rules are followed, then we have the following properties: Flux lines are in direction of E. The magnitude of the electric field is inversely proportional to the spacing between the flux lines. * This is what you will be doing in the class project. 27
Example In the class project, you will be drawing in flux lines. (The equipotential contours come from Excel.) 1 6 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 1 1 1 1 0-0.2 0.2 0.2-0.4 0.4 0.4-0.6 0.6 0.6-0.8 0.8 0.8-1 1.0 V 0 V Contour Plot Task 2 Parallel-plate capacitor region 28
Example (cont.) In the class project, you will be drawing in flux lines. 1 6 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 1 1 1 1 0-0.2 0.2-0.4 0.4-0.6 0.6-0.8 0.8-1 Contour Plot Task 2 Parallel-plate capacitor region 29
Flux Plot with Conductors Conductor Some observations: Flux lines are closer together where the field is stronger. The field is strong near a sharp conducting corner. Flux lines begin on positive charges and end on negative charges. Flux lines enter a conductor perpendicular to it. http://en.wikipedia.org/wiki/Electrostatics 30
Example of Electric Flux Plot Note: In this example, the aspect ratio L/W is not held constant! Electroporation-mediated topical delivery of vitamin C for cosmetic applications Lei Zhanga, , Sheldon Lernerb, William V Rustruma, G nter A Hofmanna a Genetronics Inc., 11199 Sorrento Valley Rd., San Diego, CA 92121, USA b Research Institute for Plastic, Cosmetic and Reconstructive Surgery Inc., 3399 First Ave., San Diego, CA 92103, USA. 31
Example of Magnetic Flux Plot Solenoid wrapped around a ferrite core (cross sectional view) Flux plots are often used to display the results of a numerical simulation, for either the electric field or the magnetic field. Magnetic flux lines Solenoid windings Ferrite core 32
Appendix: Proof of Flux Property 33
Proof of Flux Property E L NC: flux lines Through C E C n L C One small piece of the contour (the length is L) C =number of flux lines N C ( ) D n = cos L D L E l L ( ) cos D L so l L ( ) D L or l 34
Flux Property Proof (cont.) ( ) D L l E Also, L N 1/ D L C (from the property of a flux plot) Hence, substituting into the above equation, we have N L ( ) = C D L L N l C N Therefore, (proof complete) l C 35