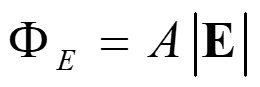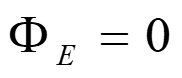Ch. 23
Electric Flux
•
Electric flux is the amount of electric field going across a surface
•
It is defined in terms of a direction, or normal unit vector,
perpendicular to the surface
•
For a constant electric field, and a flat surface, it is easy to calculate
•
Denoted by
E
•
Units of N
m
2
/C
•
When the surface is flat, and the fields are constant, you
can just use multiplication to get the flux
•
When the surface is curved, or the fields are not constant,
you have to perform an integration
Ch
. 23
Warmup 03
Ans C
Is the answer independent of the shape?
Like
example
23.4
PCV at L’institut Superieur du
Pedagogy
JIT
Quick Quiz 23.1
Ans e
Warmup 03
Solve on Board
Total Flux Out of Various Shapes
A point charge
q
is at the “center” of a (a) sphere (b) joined hemispheres
(c) cylinder. What is the total electric flux out of the shape?
q
q
q
a
a
b
Electric Flux (
Hard example)
A point charge
q
is at the center of a cylinder of radius
a
and height 2
b
.
What is the electric flux out of (a) each end and (b) the lateral surface?
q
b
b
a
b
s
r
•
Consider a ring of radius
s
and thickness
ds
lateral surface
a
z
r
top
Gauss’s Law
•
No matter what shape you use, the total electric flux out of a region
containing a point charge
q
is 4
k
e
q = q
/
0
.
Why is this true?
•
Electric flux is just measuring how many field
lines come out of a given region
•
No matter how you distort the shape, the field lines
come out somewhere
•
If you have multiple charges inside the region their effects add
•
However, charges outside the region do not contribute
q
q
1
q
2
q
3
q
4
Warmup 03
Using Gauss’s Law to find total charge
a
a
a
A cube of side
a
has an electric field of
constant magnitude |
E
| =
E
pointing
directly out on two opposite faces and
directly in on the remaining four faces.
What is the total charge inside the cube?
A) 6
Ea
2
0
B) – 6
Ea
2
0
C) 2
Ea
2
0
D) – 2
Ea
2
0
E) None of the above
JIT Quick Quiz 23.2
Ans B and D
Ans C
Ans E (B&C)
Using Gauss’s Law to find flux
A very long box has the shape of a regular pentagonal prism.
Inscribed in the box is a sphere of radius
R
with surface charge
density
. What is the electric flux out of one lateral side of the box?
End view
Perspective
view
•
The flux out of the end caps is negligible
•
Because it is a
regular
pentagon, the flux from the
other five sides
must
be the same
Using Gauss’s Law to find E-field
A sphere of radius
a
has uniform charge density
throughout. What
is the direction and magnitude of the electric field everywhere?
a
•
Clearly, all directions are created equal in this problem
•
Certainly the electric field will point away from the sphere at all points
•
The electric field must depend
only
on the distance
•
Draw a sphere of radius
r
around this charge
•
Now use Gauss’s Law with this sphere
r
Is this the electric field everywhere?
Using Gauss’s Law to find E-field (2)
A sphere of radius
a
has uniform charge density
throughout. What
is the direction and magnitude of the electric field everywhere? [Like
example
23.6
]
a
•
When computing the flux for a Gaussian surface, only include the
electric charges
inside
the surface
r
r/a
Electric Field From a Line Charge
What is the electric field from an infinite
line with linear charge density
?
•
Electric field must point away from the line charge, and depends only
on distance
•
Add a cylindrical Gaussian surface with radius
r
and length
L
•
Use Gauss’s Law
•
The ends of the cylinder don’t contribute
•
On the side, the electric field and the normal are parallel
r
L
Electric Field From a Plane Charge
What is the electric field from an infinite
plane with surface charge density
?
•
Electric field must point away from the surface, and depends only on
distance
d
from the surface
•
Add a box shaped Gaussian surface of size 2
d
L
W
•
Use Gauss’s Law
•
The sides don’t contribute
•
On the top and bottom, the electric field and the normal are parallel
Ans A
Solve on Board
Serway 23-33
Here use A X normal unit vector for A vector of text.
Really when everything in integral is constant, you can just multiply.
So, if E dot n is constant along surface – you are OK.
Gauss's Law in electromagnetism relates electric fields to electric charges. Electric flux, defined as the amount of an electric field crossing a surface, plays a crucial role in understanding the behavior of electric fields in various situations. This content delves into the principles of Gauss's Law, electric flux calculations, and practical examples for better comprehension.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Ch. 23 = A E n E Gauss's Law Electric Flux Electric flux is the amount of electric field going across a surface It is defined in terms of a direction, or normal unit vector, perpendicular to the surface For a constant electric field, and a flat surface, it is easy to calculate Denoted by E Units of N m2/C When the surface is flat, and the fields are constant, you can just use multiplication to get the flux When the surface is curved, or the fields are not constant, you have to perform an integration E dA E n = = = AE n cos AE E E n = 0 E
Ex 1 - Let there be a constant electric field in the positive x direction of magnitude 2 N/C. What is the flux through a cube that is 2m on a side sitting such that one of its sides is parallel to the x-y plane? This is like 23.4 on page 623. When would the fluc be nonzero? Work out on board. CT -1- A cylindrical piece of insulating material is placed in an external electric field, as shown. The net electric flux passing through the surface of the cylinder is Like example 23.4 A.positive. B.negative. C.zero. Ans C Is the answer independent of the shape?
PCV at Linstitut Superieur du Pedagogy
Quick Quiz 23.1 JIT Ans e
Ex- A 40 cm diameter loop is rotated in a uniform electric field until the position of maximum electric flux (through the loop) is found. The flux in this position is 5.20 x 105 Nm2/C. What is the electric field strength? Solve on Board
Total Flux Out of Various Shapes A point charge qis at the center of a (a) sphere (b) joined hemispheres (c) cylinder. What is the total electric flux out of the shape? e k q a b a = + + E n = 1 2 3 E E E e k q a 2 E 2 = = 2 EA 22 a = E n e k q a 4 dA 1 E E q = e k q q n = 2 24 a n 1 E = 2 0 a n E = E e k q + 2 = E n E e k q E E 3 E = 2 cap E lat 2 E E = e k q 4 k qb + E = 2 2 e k q e 2 2 b a k qb + q 4 = e k q + 4 e E 2 2 b a
Electric Flux (Hard example) A point charge q is at the center of a cylinder of radius a and height 2b. What is the electric flux out of (a) each end and (b) the lateral surface? = E 2 dA sds n s e k q r e k qb + = + 2 2 r s b = top E 2 E b e k q r e k qb r b = E n = = r cos r ( ) 3/2 2 3 z 2 2 n b s a q Consider a ring of radius s and thickness ds a = b a e k qb + 2 e k qbsds s + 2 = E n dA = ( k qb + 2 ) E 3/2 2 2 2 2 b s b 0 a 0 2 = + = 4 2 2 r z a 2 e k qb + = lateral surface E n = 2 k qa dz + 2 e k q E e 2 2 b b a 3 e k qa r 2 a dA adz b k qz + = E n = dA = e = e ( ) E 3/2 2 2 2 2 2 2 a b a z z b b
Gausss Law No matter what shape you use, the total electric flux out of a region containing a point charge q is 4 keq = q/ 0. Why is this true? Electric flux is just measuring how many field lines come out of a given region No matter how you distort the shape, the field lines come out somewhere E = q e k q = q 4 0 E If you have multiple charges inside the region their effects add However, charges outside the region do not contribute ( 1 E q = + q4 q ) + q q 2 3 0 E= E dA =qin = in q3 E q1 0 0 q2
Using Gausss Law to find total charge A cube of side a has an electric field of constant magnitude |E| = E pointing directly out on two opposite faces and directly in on the remaining four faces. What is the total charge inside the cube? A) 6Ea2 0 B) 6Ea2 0 C) 2Ea2 0 D) 2Ea2 0 E) None of the above 6 i = 2 in 0 2 q Ea = E E a E E E a a E ( ) = 02 2 2 = E n = 4 Ea Ea A q 0 in 0 E 1
JIT Quick Quiz 23.2 Ans B and D
CT 2 - Which of the following statements is (are) true? A.When there are more electric field lines leaving a gaussian surface than entering it then there is a net negative charge enclosed by the surface. B.Gauss's law can be used to find the electric field if the total charge inside a closed surface is known even if the distribution of that charge is not. C.The electric flux through a closed surface is completely independent of the size and shape of the surface. D.Two of the above E.None of the above Ans C
CT-3 Which of the following statements is (are) true? A.The electric field E at any point on the surface S is determined only by the charges inside S (Q1 and Q2). B.The electric flux E through surface S is determined only by the charges inside S (Q1 and Q2). C.The field E at any point on S is determined by all the charges (Q1, Q2 and Q3). D.The electric flux E through S determined by all the charges (Q1, Q2 and Q3). E.Two of the above. F.None of the above statements is true! S Q2 Q3 Q1 Ans E (B&C)
Using Gausss Law to find flux A very long box has the shape of a regular pentagonal prism. Inscribed in the box is a sphere of radius R with surface charge density . What is the electric flux out of one lateral side of the box? Perspective view The flux out of the end caps is negligible Because it is a regular pentagon, the flux from the other five sides must be the same q = End view = 2 5 4 R in 0 E ,side 0 E = 5 A = 2 4 5 R ,side 0 E ,side 0 E
Using Gausss Law to find E-field A sphere of radius a has uniform charge density throughout. What is the direction and magnitude of the electric field everywhere? Clearly, all directions are created equal in this problem Certainly the electric field will point away from the sphere at all points The electric field must depend only on the distance Draw a sphere of radius r around this charge Now use Gauss s Law with this sphere V = 0 r = E r E = q in 0 E = 3 AE n a = 3 E r 0 r E 2 3 2 4 a 4 3 0 r a Is this the electric field everywhere? E
Using Gausss Law to find E-field (2) A sphere of radius a has uniform charge density throughout. What is the direction and magnitude of the electric field everywhere? [Like example 23.6] When computing the flux for a Gaussian surface, only include the electric charges inside the surface V AE n = q = in = = 0 E E r E 0 3 2 4 r r E 4 3 E 0 = r 3 r 0 r 3 2 r 3 3 for for , . a r r r a a = 0 E r r a 0 E r/a
Electric Field From a Line Charge What is the electric field from an infinite line with linear charge density ? n E n = E r E L r r = E 2 r 0 Electric field must point away from the line charge, and depends only on distance Add a cylindrical Gaussian surface with radius r and length L Use Gauss s Law The ends of the cylinder don t contribute On the side, the electric field and the normal are parallel L da E n = 0 E = q in 0 E = E ( ) = 0EA = 2 rL 2 r 0 0
Electric Field From a Plane Charge What is the electric field from an infinite plane with surface charge density ? E E k n = E n n k = E 2 0 Electric field must point away from the surface, and depends only on distance d from the surface Add a box shaped Gaussian surface of size 2d L W Use Gauss s Law The sides don t contribute On the top and bottom, the electric field and the normal are parallel LW da E n = = q in 0 E = E ( ) = 0EA = 2 E LW 2 0 0 0
CT-4 - The electric charge per unit area is + for infinite plate 1 and for infinite plate 2.The magnitude of the electric field associated with plate 1 is ( ) and the electric field lines for this plate are as shown. When the two are placed parallel to one another, the magnitude of the electric field is A. / between, 0 outside. B. / between, /(2 ) outside. C. zero both between and outside. D. /(2 o) both between and outside. E. none of the above. Ans A
Serway 23-33 Solve on Board
