Crystal Geometry and Lattice Structures in Science
Crystal geometry involves understanding primitive lattice cells, crystal structures, lattice parameters, and Miller indices. Explore the concepts of crystallography and crystal planes in this comprehensive science study material.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
THIRD YEAR T.D.C., SCIENCE THIRD YEAR T.D.C., SCIENCE PAPER PAPER- -III, Part B III, Part B Paper Code Paper Code - - 3163
UNIT 1 : CRYSTAL GEOMETRY PRIMITIVE LATTICE CELL As observed previously, a primitive lattice cell is a type of cell which is also called a unit cell and represents the minimum volume cell which can be used to build the crystal There is a density of one lattice point per primitive cell 2
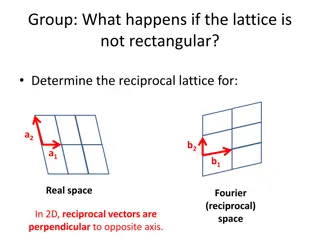
UNIT 1 : CRYSTAL GEOMETRY Primitive Cell PRIMITIVE LATTICE CELL A primitive lattice cell (unit cell) represents the minimum volume cell which can be used to build the crystal Fig. 2 In Fig. 2, choosing a corner as the origin, the three edge vectors {a, b, c}from the origin define coordinate system The three lengths a, b, c and the three inter-axial angles (i.e., the angle between the axes) , , are called the lattice parameters a crsytallographic 3
UNIT 1 : CRYSTAL GEOMETRY PRIMITIVE LATTICE CELL If we consider a parallelepiped (as given in the figure for a simple cubic lattice cell), although there are 8 corners of the parallelepiped, each atom at a corner is shared by the 8 cells that touch there. The volume Vc of a cell with axes a, b, c is Vc = ? ?.? 4
UNIT 1 : CRYSTAL GEOMETRY PRIMITIVE LATTICE CELL A way of choosing a cell of volume Vc called the primitive or Wigner-Seitz primitive cell is by using the following procedure: Draw lines from a given lattice point to all nearby lattice points. Draw perpendicular bisectors to each of these lines The volume enclosed in this way would be the smallest and is that of the Wigner-Seitz primitive cell as given in the Figure 5
UNIT 1 : CRYSTAL GEOMETRY CRYSTAL MILLER INDICES PLANES AND The crystal lattice may be regarded as made up of an infinite set of parallel equidistant planes passing through the lattice points. d These planes are known as lattice planes. In figure given above, the straight lines joining the lattice different lattice planes. In other words, the planes passing through lattice points are called lattice planes . points represent 6
UNIT 1 : CRYSTAL GEOMETRY CRYSTAL PLANES AND MILLER INDICES The orientation of planes or faces in a crystal can be described in terms of their intercepts on the three axes. Miller introduced a system to designate a plane in a crystal. He introduced a set of three numbers to specify a plane in a crystal. This set of three numbers is known as MillerIndices of the concerned plane. Miller indices are defined as the reciprocals of the intercepts made by the plane on the three axes. 7
UNIT 1 : CRYSTAL GEOMETRY Procedure for finding Miller Indices Determine the intercepts of the plane along the axes X,Y and Z in terms of the lattice constants a,b, c. Determine the reciprocals of these numbers. Find the least common denominator (lcd) and multiply each by this lcd. The result is written in brackets as (h k l) and is known as the `Miller Indices of the plane. 8
UNIT 1 : CRYSTAL GEOMETRY Z Procedure for finding Miller Indices: EXAMPLE: C In the this figure, plane ABC has intercepts of 2 units along X-axis, 3 units along Y-axis and 2 units along Z-axis. The intercepts are 2, 3 and 2 on the three axes and the reciprocals are 1/2, 1/3 and 1/2. The lcd of 2, 3, 2 is 6. A B Multiplying each reciprocal by the least common denominator (lcd) i.e, 6, we get, 3,2 and 3. Y X Thus the Miller indices for the plane ABC is (3 2 3) or (h k l) is (3 2 3) 9
UNIT 1 : CRYSTAL GEOMETRY Z Important Features of Miller Indices C For cubic crystals especially, the important features of Miller indices are: A plane which is parallel to any one of the co- ordinate axes has an intercept of infinity ( ). A B Y Therefore the Miller index for that axis is zero; i.e. for an intercept at infinity, the corresponding index is zero (since the reciprocal, i.e., 1/ = 0) X 10
UNIT 1 : CRYSTAL GEOMETRY Z EXAMPLE: (100) plane : Plane parallel to Y and Z axes As an example, in the given figure, consider the shaded plane X In this plane, the intercept along X axis is 1 unit. The plane is parallel to Y and Z axes. Therefore it does not cut the Y or Z axes at any point. Y So, the intercepts along Y and Z axes are . Therefore, the intercepts are 1, and . The reciprocals of the intercepts are = 1/1, 1/ and 1/ . Therefore the Miller indices for the shaded plane are (1 0 0) 11
UNIT 1 : CRYSTAL GEOMETRY Some more examples of Miller Indices 12