Constructing Perpendiculars: Shortest Distance to a Point

Learn how to find the shortest distance from a point to a line, ensuring the path taken is efficient and direct. By constructing a perpendicular from the point to the line, you guarantee the shortest possible route, creating a right angle with the line. Explore the process of constructing perpendiculars visually to understand why this method yields the shortest distance.

• Perpendicular Construction
• Shortest Distance
• Geometry Concepts
• Right Angle

ursa Follow

Uploaded on Aug 07, 2024 | 2 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

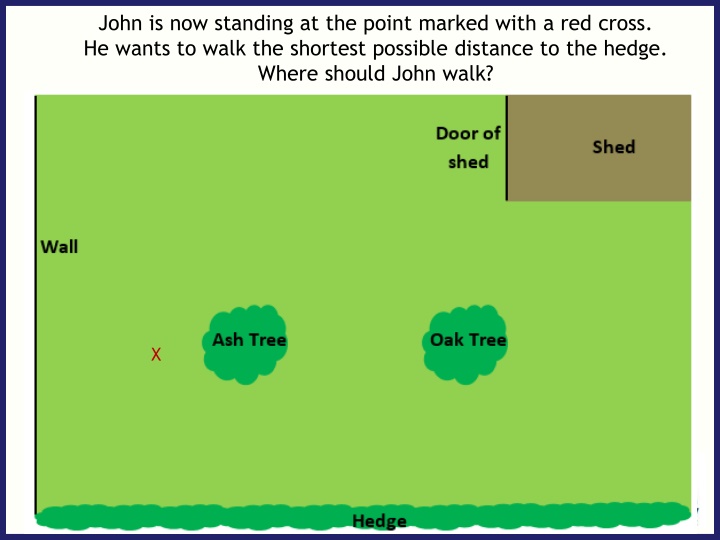
1. John is now standing at the point marked with a red cross. He wants to walk the shortest possible distance to the hedge. Where should John walk? X

2. Why wouldnt John walk this way to the hedge? X

3. How can we guarantee that we have drawn the shortest possible distance? X

4. The shortest possible route makes a right angle with the hedge X

5. This type of construction is referred as a perpendicular from a point.

6. When constructing a perpendicular from a point the new path is the shortest possible distance from the point to the line

7. Constructing a Perpendicular from a Point M P Q

8. Constructing a perpendicular from a point How can we show that the new line is the shortest possible distance from the point M to the line PQ? M P Q

9. Constructing a perpendicular from a point M P Q Measure it!

10. Constructing a Perpendicular from a Point M P Q

11. Constructing a Perpendicular from a Point M P Q Would this line be shorter?

12. Constructing a Perpendicular from a Point M P Q Why not?

13. The Perpendicular From a Point Construct the perpendicular from each of the given points on the worksheet. Complete your constructions on the worksheet Leave in your construction lines

14. Construct a perpendicular from a point on the following:

15. Construct a perpendicular from a point on the following:

16. Construct a perpendicular from a point on the following:

17. Challenge: Construct a line perpendicular to AB that passes through P Construct a line perpendicular to CD that passes through P What is the name of the resulting quadrilateral? Measure its side lengths with a ruler and calculate its area and perimeter