Comparing Energy Levels in Atomic and Molecular Systems
E=0
*Energy in units of h
2
/8m
e
L
2
~
1.5*10
-18
J
n=1
n=2
n=3
n=4
n=5
E*
25
16
9
4
1
Energy Manifold: 1 electron in ground state
in box with L=2*10
-10
m (0.2 nm)
m
e
~1*10
-30
kg
E=0
*Energy in units of h
2
/8m
e
L
2
=1.8*10
-19
J
n=1
n=2
n=3
n=4
n=5
E*
25
16
9
4
1
Energy Manifold assuming butadiene
e
-
are in box the length of butadiene (p. 83)
L=5.78*10
-10
m
m
e
~10
-30
g
Assume
4
electrons
resonate freely
E=hf=
5
Comparison of calculated 1D
particle in box magnitudes with real
atomic scale systems
1 electron in 2*10
-10
m box
E(n=1)
1.5*10
-18
J
1 electron in 2 *10
-10
m
diameter orbit around H
atom
2.2*10
-18
J
E
for n=2
n=3 jump in
model for butadiene
(L=5.78*10
-10
m)
5*1.8*10
-19
=9.0*10
-19
J
Observed HOMO-
LUMO
transition
energy
for butadiene
9.1*10
-19
J
System considered
P(x)dx
= 2/L sin
2
(n
x/L) dx
(x) =
2/L sin (n
x/L)
Key Particle-in-box results
1)Normalized Wave function
2) Eigen energy ,
E
E
=n
2
h
2
/8m
e
L
2
3) Probability density,
P(x)
Switch slide orientation in
design
1D particle-in-a-box P(x) vs. n: at high n…the system converges to
continuum
P(x) for 1D box at
n=100,L=1
2D particle-on-a ring predictions for simple porphyrin (26
electrons* running free
(See also:
Supplement 2:
The 2-D particle in-a-box applied to a real
molecule)
L
L
* Assumes lone pair and inner
electrons are part of
delocalization
L = 1*10
-9
m
HOMO=Highest Occupied Molecular Orbit
LUMO = Lowest Unoccupied Molecular Orbit
E
predicted
= k*[(3
2
+4
2
)-(4
2
+2
2
)] = k[25-20] =5k =
1.52*10
4
cm
-1
E =k(n
x
2
+n
y
2
)
= 3.0375*10
3
(n
x
2
+n
y
2
) cm
-1
E
observed
=
=1.70*10
4
cm
-1
After solving 2D problem: (see supplement 2)
Comparing energy levels of electrons in different scenarios, including 1D particle in a box, electrons around atoms, and within molecular structures like butadiene and porphyrin. The calculated and observed energy transitions provide insights into the behavior of particles within confined spaces.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
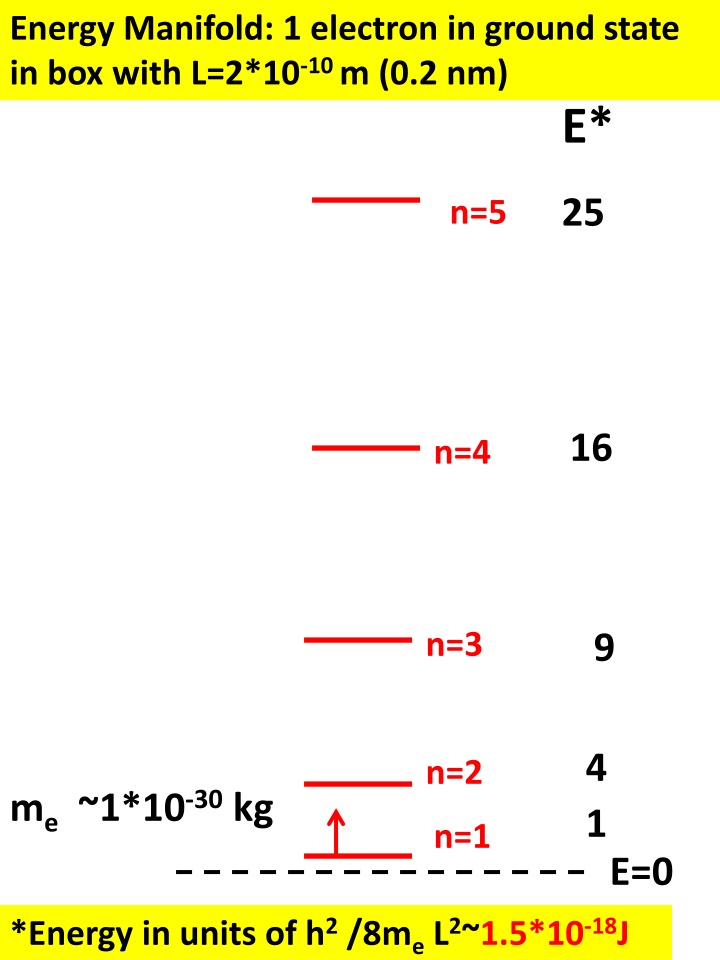
Energy Manifold: 1 electron in ground state in box with L=2*10-10 m (0.2 nm) E* 25 n=5 16 n=4 n=3 9 4 1 n=2 me ~1*10-30 kg n=1 E=0 *Energy in units of h2 /8me L2~1.5*10-18J
Energy Manifold assuming butadiene e- are in box the length of butadiene (p. 83) E* Assume 4 electrons resonate freely 25 n=5 C C C C C C C C L=5.78*10-10 m 16 n=4 n=3 9 E=hf=5 n=2 me ~10-30 g 4 n=1 1 E=0 *Energy in units of h2 /8meL2=1.8*10-19 J
Comparison of calculated 1D particle in box magnitudes with real atomic scale systems E(n=1) 1.5*10-18 J System considered 1 electron in 2*10-10 m box 1 electron in 2 *10-10 m diameter orbit around H atom 2.2*10-18 J E for n=2 n=3 jump in model for butadiene (L=5.78*10-10 m) 5*1.8*10-19 =9.0*10-19 J Observed HOMO- LUMO transition energy for butadiene 9.1*10-19 J
Key Particle-in-box results 1)Normalized Wave function (x) = 2/L sin (n x/L) 2) Eigen energy , E E=n2 h2 /8meL2 3) Probability density, P(x) P(x)dx = 2/L sin2 (n x/L) dx
Switch slide orientation in design
1D particle-in-a-box P(x) vs. n: at high nthe system converges to continuum P(x) for 1D box at n=4, L=1 P(x) for 1D box at n=1, L=1 2 2 1.8 1.8 1.6 1.6 1.4 1.4 1.2 1.2 P(x) P(x) 1 1 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 0 0 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 x x P(x) for 1D box at n=100,L=1 P(x) for 1D box at n=2, L=1 2 1.8 1.6 1.4 1.2 P(x) 1 0.8 0.6 0.4 0.2 0 0 0.2 0.4 0.6 0.8 1 x
2D particle-on-a ring predictions for simple porphyrin (26 electrons* running free (See also: Supplement 2: The 2-D particle in-a-box applied to a real molecule) L L N NH H N N L = 1*10-9 m * Assumes lone pair and inner electrons are part of delocalization
After solving 2D problem: (see supplement 2) E =k(nx2 +ny2) = 3.0375*103 (nx2 +ny 2) cm-1 HOMO=Highest Occupied Molecular Orbit LUMO = Lowest Unoccupied Molecular Orbit Epredicted= k*[(32+42)-(42+22)] = k[25-20] =5k = 1.52*104 cm-1 Eobserved = =1.70*104 cm-1
