Chapter 5 - Gases
This study explores the impact of quality assurance on student grades in online course design. It discusses limitations, controlled variables, and components needed for similar research, focusing on research questions, data analysis, and partnerships within the educational technology sector.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Chapter 5 - Gases DE Chemistry Dr. Walker
Properties of Gases Gases expand to fill their containers Gases are fluid they flow Gases have low density 1/1000 the density of equivalent moles of liquid or solid Gases are compressible
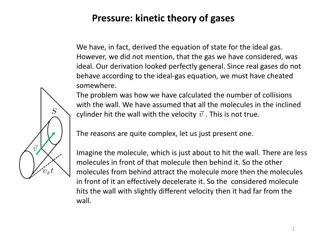
Its all in your mind Ideal gases are imaginary gases that fit all of the assumption of the kinetic molecular theory Gases consist of tiny particles that are far apart relative to their size (this is true ) Collisions between gas particles and between particles and the container walls are elastic (lose no kinetic energy in the process) .our big assumption!
More on Ideal Gases Gas particles are in constant, rapid motion and possess kinetic energy as a result There are no forces of attraction between gas particles (assumption .the attractions are small, but present) The average kinetic energy of gas particles depends on temperature, not the identity of the particle (partially true .but still an assumption)
Youve Got Me Under Pressure Force is acceleration of a mass Force is measured in Newtons (N) 1 N = 1 kg x m/s2 Pressure is force exerted over a specific area, in this case, with the walls of a container The SI unit for pressure is the Pascal (Pa) 1 Pa = 1 N/m2
Units of Pressure Unit Pascal Symbol Pa Definition/Relationship SI pressure unit 1 Pa = 1 newton/meter2 Pressure that supports a 1 mm column of mercury in a barometer Average atmospheric pressure at sea level and 0 C 1 torr = 1 mm Hg Millimeter of mercury mm Hg Atmosphere atm Torr torr
Measuring Pressure The first device for measuring atmospheric pressure was developed by Evangelista Torricelli during the 17thcentury. The device was called a barometer Baro = weight Meter = measure
Why Kelvin? Remember two things The Kelvin scale is directly proportional to kinetic energy Based on the equations you will learn, negative temperatures can cause calculations yielding negative pressures and/or volumes which are not possible Absolute zero = 0 K = -273 C = -459 F
STP Standard Temperature and Pressure 273 K (0 oC) 1 atm 101.3 kPa 14.7 psi (lbs/in2) 760 mm Hg (760 torr)
Boyles Law Pressure is inversely proportional to volume when temperature is held constant. P1V1 = P2V2
Side Note to Boyles Law It was the experiments of Boyle that showed that showed that at low pressures PV = constant This constant was equal to 22.4 L . Atm. This is the origin of the 22.4 number you learned last year. Avogadro s discovery of 1 mole being equal to a equal volume of any gas led to the idea of 1 mole = 22.4 L at STP. It is only valid at STP and low pressures
Charles Law The volume of a gas is proportional to Kelvin temperature at constant pressure Extrapolates to zero at zero Kelvin (this has never been accomplished experimentally) V= V 1 2 T T 1 2
Gay-Lussacs Law The pressure and temperature of a gas are directly proportional at constant volume Temperature must be in Kelvin P= P 1 2 T T 1 2
Combining Boyle, Charles, and Gay- Lussac The Combined Gas Law!! P V P V = 1 T 1 2 T 2 1 2 Relates temperature, pressure, and volume of a fixed amount of gas
Avogadros Law For a gas at constant temperature and pressure, the volume is directly proportional to the number of moles of gas (at low pressures) V = an a = proportionality constant V = volume of gas n = number of moles of gas
Ideal Gas Law Combining Avogadro, Boyle, Charles, and Gay- Lussac . PV = nRT P = pressure (typically in atm) V = volume in liters n = moles R = universal gas constant (0.08206 L. atm/mol . K) T = temperature (Kelvin) Works best at pressures under 1 atm
Real Gases At high pressure (smaller volume) and low temperature (attractive forces become important) you must adjust for non-ideal gas behavior using van der Waal s equation + 2 n V = ( ) P a x V nb nRT obs corrected pressure corrected volume Videal Pideal
Gas Density Density = mass/volume For gases this becomes D = molar mass/molar volume (22.4 L @ STP)
Density and the Ideal Gas Law When combining density with the Ideal Gas Law, and rearranging algebraically: M = Molar Mass P = Pressure R = Gas Constant T = Temperature in Kelvins
Gas Stoichiometry If reactants and products are at the same conditions of temperature and pressure, then mole ratios of gases are also volume ratios. 3 H2(g) + N2(g) 2NH3(g) 3 moles H2 + 1 mole N2 2 moles NH3 3 liters H2 + 1 liter N2 2 liters NH3
Gas Stoichiometry Example Example: N2 + 3 H2 2 NH3 How many liters of ammonia could be produced from 6 liters of N2 and excess H2?
Gas Stoichiometry Example Example: N2 + 3 H2 2 NH3 How many liters of ammonia could be produced from 6 liters of N2 and excess H2? 6 L N2 2 L NH3 = 12 moles NH3 1 L N2
Gas Stoichiometry The Old Way 2 KClO3 (s) 2 KCl (s) + 3 O2 (g) How many liters of oxygen are produced from the decomposition of 244 g KClO3?
Gas Stoichiometry The Old Way 2 KClO3 (s) 2 KCl (s) + 3 O2 (g) How many liters of oxygen are produced from the decomposition of 244 g KClO3? Using proportion 244 g KClO3 Liters O2 3 mole O2 x 22.4 L O2 2 mole KClO3 x 122.55 g/mole KClO3 Liters O2 = 66.90 L (answer!!)
Gas Stoichiometry Dimensional Analysis 2 KClO3 (s) 2 KCl (s) + 3 O2 (g) How many liters of oxygen are produced from the decomposition of 244 g KClO3? 244 g KClO3 1 mol KClO3 122.55 g KClO3 3 mol O2 22.4 L O2 2 mol KClO3 1 mol O2 = 66.9 L O2
Gas Stoichiometry Remember that 1 mole = 22.4 L applies ONLY at STP. If the gas exists at another set of conditions, you must use the Ideal Gas Law to find your volume Find volume first if starting with a gas Find volume last if ending with a gas Proportion method doesn t really work here
Volume of Gas as a Product How many liters of oxygen gas, at 37.0 C and 0.930 atmospheres, can be collected from the complete decomposition of 50.0 grams of potassium chlorate? 2 KClO3(s) 2 KCl(s) + 3 O2(g)
Volume of Gas as a Product How many liters of oxygen gas, at 37.0 C and 0.930 atmospheres, can be collected from the complete decomposition of 50.0 grams of potassium chlorate? 2 KClO3(s) 2 KCl(s) + 3 O2(g) 50.0 g KClO3 1 mol KClO3 3 mol O2 0.612 = mol O2 122.55 g KClO3 2 mol KClO3
Volume of a Gas as a Reactant How many grams of magnesium can react in a closed container of 1 liter of oxygen gas at 25 oC and 0.980 atm?
Volume of a Gas as a Reactant How many grams of magnesium can react in a closed container of 1.00 liter of oxygen gas at 25 oC and 0.980 atm? 2 Mg + O2 2 MgO Find moles of oxygen with ideal gas law (0.980 atm)(1.00 L) VP L atm =RT = n (0.0821 )(298) = 0.400 moles mol K
Volume of Gas as a Reactant How many grams of magnesium can react in a closed container of 1.00 liter of oxygen gas at 25 oC and 0.980 atm? 2 Mg + O2 2 MgO Plug into dimensional analysis 2 mol Mg 0.0400 moles O2 24.31 g Mg = 1.95 g Mg 1 mol Mg 1 mol O2
Daltons Law of Partial Pressures For a mixture of gases in a container, PTotal = P1 + P2 + P3 + . . . This is particularly useful in calculating the pressure of gases collected over water.
Kinetic Molecular Theory ki net ic 1. pertaining to motion. 2. caused by motion. characterized by movement: Running and dancing are kinetic activities. 3. Origin: 1850 55; < Gk k n tik s moving, equiv. to k n - (verbid s. of k ne n to move) + -tikos Source: Websters Dictionary
Properties of Gases Gases expand to fill their containers Gases are fluid they flow Gases have low density 1/1000 the density of equivalent moles of liquid or solid Gases are compressible
Kinetic Molecular Theory (Ideal Gases) Particles of matter are ALWAYS in motion Volume of individual particles is zero. Collisions of particles with container walls cause the pressure exerted by gas. Particles exert no forces on each other. Average kinetic energy is proportional to Kelvin temperature of a gas.
Kinetic Energy of Gases At the same conditions of temperature, all gases have the same average kinetic energy. 1mv KE= m = mass v = velocity 2 2 Different gases have different masses, so if KE is the same, the velocities must be different! Smaller mass means higher velocity to reach the same KE At the same temperature, small molecules move FASTER than large molecules
Temperature 3 2 = ( ) KE RT avg Kelvin temperature is an index of the random motions of gas particles (higher T means greater motion.) This is derived from the Ideal Gas Law and explained on p. 203-204. The units will not cancel when plugging in numbers.
Diffusion Diffusion describes the mixing of gases. The rate of diffusion is the rate of gas mixing. Diffusion is the result of random movement of gas molecules The rate of diffusion increases with temperature More movement, more diffusion Small molecules diffuse faster than large molecules Faster movement, more overall diffusion
Effusion Effusion: describes the passage of gas into an evacuated chamber.
Grahams Law of Effusion Distance traveled by gas 1 M = 2 Distance traveled by gas 2 M 1 M1 = Molar Mass of gas 1 M2 = Molar Mass of gas 2