Central Angles and Tangents in Polygons

Properties of central angles and tangent lines to determine missing angles in inscribed and circumscribed polygons. Understand definitions and relationships between polygons and circles using inscribed and circumscribed concepts.

• Polygons
• Central Angles
• Tangent Lines
• Circles
• Inscribed

fort_ll Follow

Uploaded on Feb 18, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

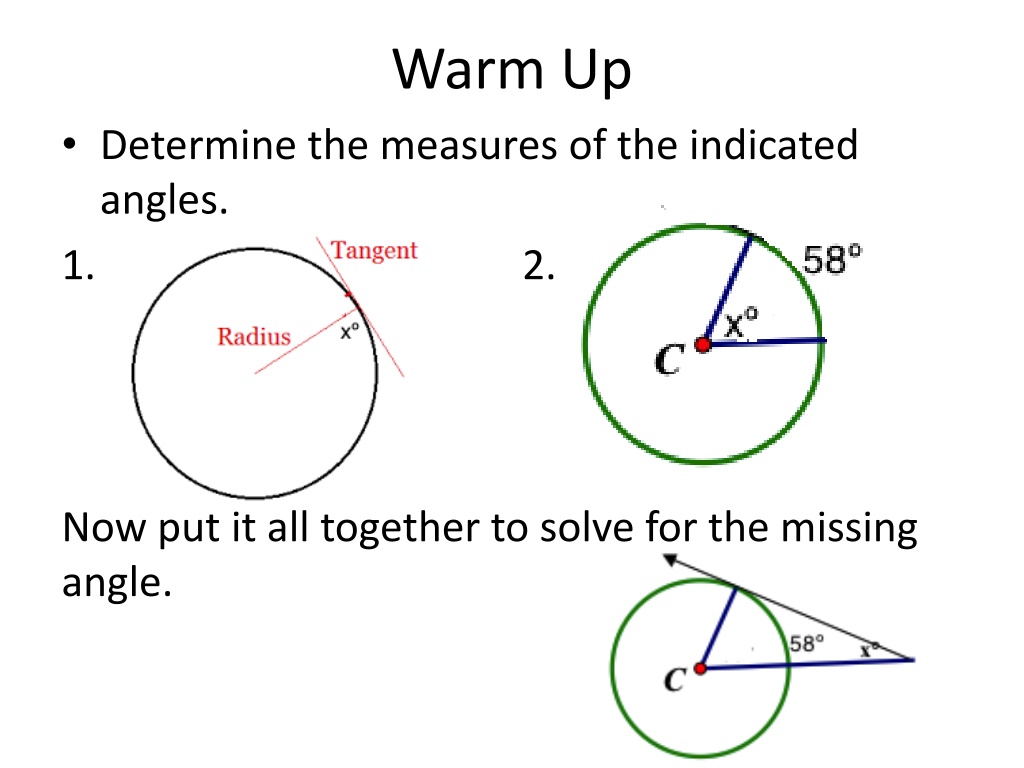
1. Warm Up Determine the measures of the indicated angles. 1. 2. Now put it all together to solve for the missing angle.

2. Unit 6 Day 3 Inscribed and Circumscribed

3. Todays Objectives Students will use properties of Central angles and Tangent lines to solve for missing parts Students will define inscribed and circumscribed polygons Students will explore properties of Inscribed and Circumscribed Triangles and Quadrilaterals

4. Using Properties of Central Angles and Tangent Lines Use the properties of Tangent Lines, Central Angles, and Inscribed Angles to solve for the missing parts

5. Defining Inscribed and Circumscribed Polygons Guided Notes Definitions Inscribed: A polygon is inscribed in a circle if all of the vertices lie on the circle. Circumscribed: A polygon is circumscribed about a circle if each side is tangent to the circle.

6. Exploration Use the properties of inscribed angles to find the missing angles Given: m ADC=60 , mBC=40 and mCD=110 , find m ABC. Then find m BCD and m DAB m ABC =_________ m BCD =_________ m DAB =_________ What do you notice about opposite angles in the quadrilateral? Supplementary About the sum of all angles? 360 Therefore, opposite angles of an inscribed quadrilateral are supplementary!

7. Inscribed or Circumscribed? Describe the relationship between the polygon and the circle using inscribed and circumscribed ?

8. Inscribed or Circumscribed? Describe the relationship between the polygon and the circle using inscribed and circumscribed ?

9. Inscribed or Circumscribed? Describe the relationship between the polygon and the circle using inscribed and circumscribed ?

10. Relationships Triangle Inscribed in a Circle http://www.geogebratube.org/student/m34411 7 Triangle Circumscribed about a Circle http://www.geogebratube.org/student/m34410 5

11. Homework