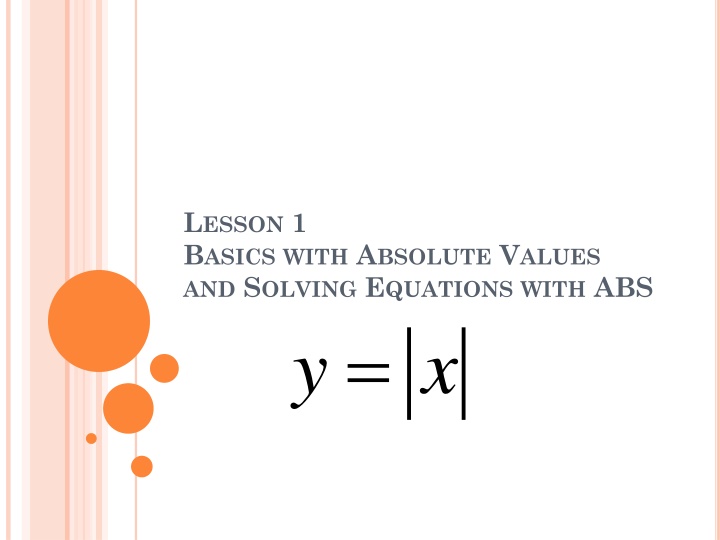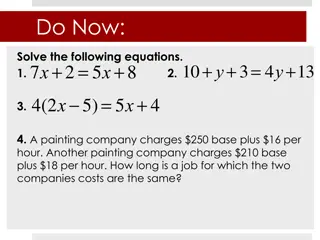Basics of Absolute Values and Solving Equations

Slide Note

Absolute value notation represents the distance from zero, with positive numbers staying positive and negative numbers becoming positive. Learn definitions, evaluations, comparisons, and solving equations involving absolute values in this comprehensive lesson.

bhan Follow

Uploaded on Mar 04, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

Download Presentation

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

E N D

Presentation Transcript

LESSON 1 BASICS WITH ABSOLUTE VALUES AND SOLVING EQUATIONS WITH ABS y = x

WHAT IS AN ABSOLUTE VALUE? The Absolute value notation is defined as the distance of any value from zero 5 5 = 6 =6 The Absolute value of a positive number stays positive, but the ABS of a negative number becomes positive Evaluate the following: ) 19 i = 19 = 81 ) 81 iii = ) 20 ) 32 = ii iv 20 32

DEFINITIONOFANABSOLUTE VALUE: There are two ways to define what an absolute value is in senior math courses: If x is greater than zero, then the abs of x will just be x (stays positive) , , x if x 0 0 x if x = x If x is less than zero, then the abs of x will be x times negative one. A negative value times negative one stays positive The second definition of an ABS value: Despite whether if x is negative or positive, when we square it, it will always be a positive = 2 x x When you square root it again, it goes back to the original value, but in positive form The square root of a positive number will always be positive only, unless it used for solving x2 ( ( ) ) 2 = = 25 5 5 25 2 = 7 = 49 49 7

EVALUATING ABS EXPRESSIONS: ) 12 317 21 = 12 3 4 = 1 12 = c 42 12 54 = 54 = ) 25 17 ) a b 12 3 4 ( ) = = 25 8 1 7 ( ) 2 = 0 318 24 + ( ) ) 5 7 e 2 ) 4 32 45 18 d ( ) ( ) 7 3 6 = 18 5 = + 16 = = + 3 6 5 7 ( ) 2 = 4 13 18 + 5 ( ) = 4 169 1 8 7 = = 676 1 8 = 16 658

Which is bigger? 132 OR 178 23 2 23 OR ( ) 2 13 48 ( ) OR 2 13 13 OR

Example 2: Order the numbers from least to Greatest. 7.5, 8.2 , 3.4, 14.6 , 4.3, 6.7 ,12.9 ) a 4.3, 3.4, 6.7 ,7.5, 8.2 , 12.9, 14.6 ) 5.6, 2.1,13.4, 24.5, 12.3, 36.8, 25.9 b 25.9, 12.3, 2.1,5.6,13.4, 24.5, 36.8

SOLVING EQUATIONSWITH ABS VALUE Given the equation below, we know that there are two values of x Therefore, x can both 10 and -10 In this next equation, the stuff inside the abs value can be either 3 or -3 2 cases! Solve each of these cases for x and then check your answer by plugging it back in Likewise, in this case example, there are also 2 cases! When you plug both answers back in, only one of them is a correct answer 10 x = 5 x = x = 5 x 8 x = x = = 4 Root = 4 2 x x 2 = 4 3 x 4 = Ext x 4 4 3 = = 2 x x x 3 5 3 = 10 10 = 3x 2 10 1 0 = x x = 10, 10

Practice: Solve for x, indicate if there are any extraneous roots 5 12 x + = 2 4 x = + = 9 2 7 4 3 0 x x = = 2 2 2 9 9 0 12 4 x x

x = x + = 2 4 9 5 12 x = x = 6.5 2 4 x = x = Ext Root 9 5 2.5 2 4 9 x + = x + = 5 x = 12 17 5 x = 12 7 x = 2 Check: Check: ( ) x 13 = = + = = = 6.5 4 9 17 5 12 12 12 + = 7 5 12 1 12 = 2 ( ) = = 2.5 = 2 4 9 9 9 12 12 4 9 9 9 YES! YES! YES! When checking your answers, No! this is an extraneous root!! + = 2 7 make sure to plug it back into the original equation!!! Not the eq in the 2nd row!! 7 4 x 4 3 0 x 3 = 2 Since the right side is negative, both your answers will be extraneous. Therefore, No Solutions! The other side of the abs value equation, must always be positive.