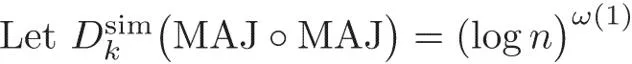Advanced Complexity Conjectures on Protocol Design
Explore advanced complexity conjectures and protocol designs in the realm of computational theory, discussing topics such as the power of super-log number of players, block composition, low-degree polynomials, and polynomial fantasies. Delve into the complexities of MAJ.MAJ, SYM, and more, while considering upper bounds and key results from notable researchers.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
The Power of Super-Log Number of Players Arkadev Chattopadhyay (TIFR, Mumbai) Joint with: Michael Saks (Rutgers)
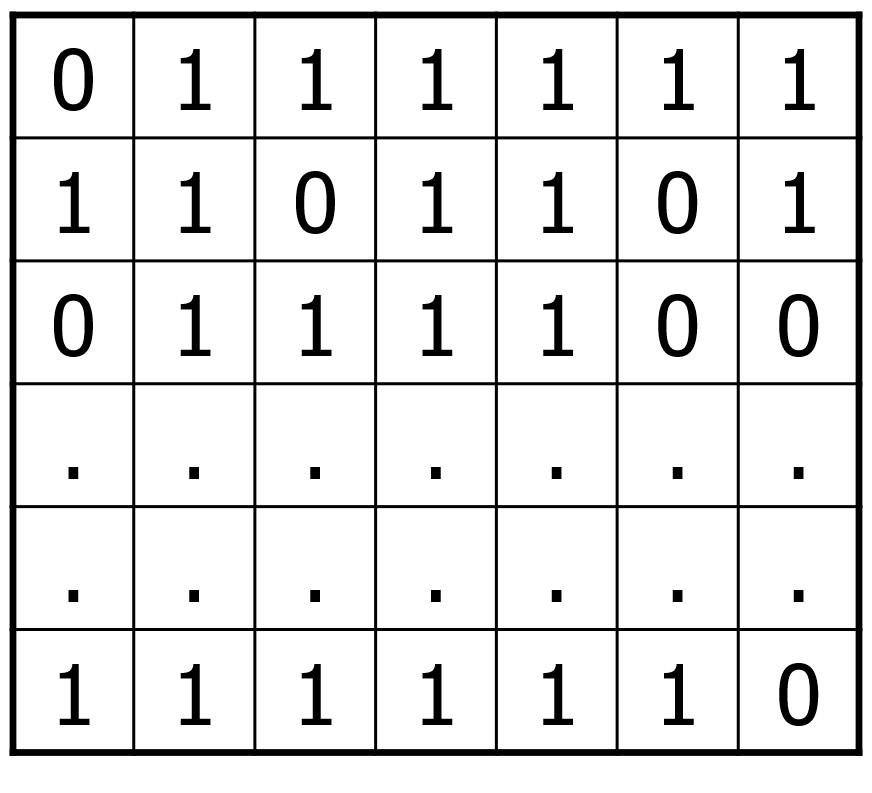
A Conjecture g:{0,1}k! {0,1} . f:{0,1}n! {0,1} (f g) (X1,X2, ,Xk) = f(g(C1),g(C2), ,g(Cn)) 0 0 1 0 1 1 0 Question: Complexity of (MAJ MAJ)? 0 1 1 1 1 1 1 1 1 0 1 1 0 1 0 1 1 1 1 0 0 . . . . . . . . 1 1 1 1 1 1 0 X1 X2 Observation: X3 ) MAJ MAJ ACC0 a la Beigel-Tarui 91 . . . . . . ) MAJ ACC0 Xk Proposed by Babai-Kimmel-Lokam 95 n
Some Upper Bounds k 3 Popular Names Deterministic (n/2k + k log n ). {GIP, Disj, } SYM AND Grolmusz 91, Pudlak Almost- Simultaneous O(k.(log n)2), k log n + 2. {GIP, MAJ MAJ, Disj } SYM g g: compressible and symmetric Babai-Gal-Kimmel-Lokam 02 Simultaneous O(k.(log n)2), k log n + 4. SYM ANY Ada-C-Fawzi-Nguyen 12 Simultaneous
Block Composition g:{0,1}k r! {0,1}. f:{0,1}n! {0,1} (fn gr) (X1,X2, ,Xk) = f(g(A1),g(A2), ,g(An)) n = 2 r = 3 Conjecture: A1 A2 0 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 1 0 . . . . . . 1 1 1 1 1 0 X1 X2 Fact: X3 ) MAJ ACC0 . . . . . . Babai-Gal-Kimmel-Lokam 02 Xk Still Open! Even for interactive protocols
Our Result Theorem: SYMn ANYr has a 2-round k-party deterministic protocol of cost r = O(log log n) when, Remark 1: First protocol for r > 1. Remark 2: Corollary: MAJ MAJr has efficient protocol when r is poly-log and k is a sufficiently large poly-log.
Main Ingredients Computing k-1 degree polynomials is easy for k- players. (Goldman-Hastad 90 s) Degree reduction by basis change. (New Idea)
Low degree Polynomials Bob, Charlie Bob, Alex Alex Alice Alice, Charlie x3x5x7 x6x10x11 x2x8x9 x1x4x12 Alice Bob Cost = O(k k log|F F|) Simultaneous k k-party deterministic protocol deg(P P) = 3 k k = 4 > deg(P P) Charlie Alex
A Polynomial Fantasy g:{0,1}k! {0,1} Fp. Prime p > n n f:{0,1}n! {0,1} g(X) P(X1, ,Xk) deg(P) k k P Phigh(X) + Plow(X) deg < k k deg = k k (SYM g) (C1,C2, ,Cn) = easy k-player protocol of cost = k.log(p) Bad Fantasy: Phigh(Ci) = 0 for all i !!
Shifted Basis u-shifted u u = 0k k gives standard basis Fact: Bu is a basis for every u2 {0,1}k Def: u is good for A if for all column C of A, u and C agree on some co-ordinate. no agreement 0 1 0 1 0 1 1 0 0 0 1 1 0 1 1 1 1 0 0 0 A 1 0 0 0 Example: bad good
Good is Really Good u u u u (SYM g) (C1,C2, ,Cn) = easy k-player protocol of cost log(p) Bad Zeroed out! Apply u u -shift u u Fact: Phigh(C) = 0 for all C if u u is good for A.
Good Shifts Are Aplenty Observation: If k log n + 1, Player k spots many good shifts. Protocol: Player k announces a good shift u u. Cost = k - 1 Simultaneous! All players compute their portions using u u. Cost = k log(p) = O(k log n) Extends to r = O(log log n).
Future Direction Can we go to r = O(log n)? Is ? Thank You!